✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Difícil)
Na figura abaixo, temos um quadrado [tex]ABCD[/tex] de lado [tex]2 \, \text{cm}[/tex]; [tex]E[/tex] é o ponto médio do segmento [tex]AB[/tex] e [tex]F[/tex] é um ponto entre [tex]E[/tex] e [tex]D[/tex].
Se os segmentos [tex]CF[/tex] e [tex]DE[/tex] são perpendiculares, determinar a área do quadrilátero [tex]BCFE[/tex].
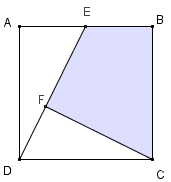
Solução 1
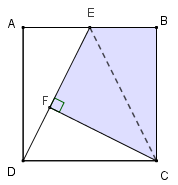
- Os dados do problema não nos permitem identificar o tipo do quadrilátero [tex]BCFE[/tex]; assim, vamos traçar o segmento [tex]EC[/tex] e dividi-lo nos triângulos [tex]EFC[/tex] e [tex]ECB[/tex], conforme mostra a figura ao lado.
Aproveitando a figura, perceba que, utilizando o Teorema de Pitágoras, podemos obter facilmente os comprimentos dos segmentos [tex]EC[/tex] e [tex]ED[/tex], já que se esse comprimento for [tex]x \, \text{cm}[/tex], então [tex]x^2=2^2+1^2=5[/tex] e, com isso, temos que [tex]\boxed{x=\sqrt{5} \, \text{cm}} \, . \quad \textcolor{#800000}{(i)}[/tex]
- Mas o que precisamos é da área do quadrilátero [tex]BCFE[/tex] e esta será a soma das áreas dos triângulos [tex]EFC[/tex] e [tex]ECB[/tex].
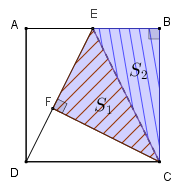
Assim, se [tex]S[/tex] for a área de [tex]BCFE[/tex] , então:
[tex]\qquad \boxed{S=S_1+S_2} \, \quad \textcolor{#800000}{(ii)}[/tex],
onde [tex]S_1[/tex] e [tex]S_2[/tex] são as áreas dos triângulos [tex]EFC[/tex] e [tex]ECB \, [/tex], respectivamente.
Perceba que [tex]ECB[/tex] é um triângulo retângulo de catetos medindo [tex]1[/tex] e [tex]2[/tex] centímetros, logo a área [tex]S_2[/tex] é dada por
[tex]\qquad \boxed{S_2= \dfrac{1\times 2}{2}=1 \, \text{cm}^2} \, \quad \textcolor{#800000}{(iii)}[/tex].
Agora, resta apenas calcular [tex]S_1.[/tex]
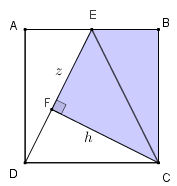
- Para o cálculo de [tex]S_1 \, [/tex] precisamos obter os comprimentos dos segmentos [tex]EF[/tex] e [tex]CF[/tex] e para isso vamos explorar o triângulo [tex]EDC.[/tex]
Da figura ao lado, observamos que a área do triângulo [tex]EDC[/tex] é [tex]\dfrac{2\times 2}{2}=2 \, \text{cm}^2[/tex] e que essa área pode também ser calculada utilizando-se como base o segmento [tex]ED[/tex] e como altura o segmento [tex]CF.[/tex] Dessa forma, segue que:
[tex]\qquad 2= \dfrac{base \times altura}{2}= \dfrac{x \times h}{2}= \dfrac{\sqrt{5} \times h}{2}[/tex]
donde concluímos que [tex]\boxed{h= \dfrac{4}{\sqrt{5}} \, \text{cm}}. \, \quad \textcolor{#800000}{(iv)} [/tex]
Para obtermos o comprimento do segmento [tex]EF[/tex], basta observar que o triângulo [tex]EFC[/tex] é retângulo, logo:
[tex]\qquad z^2+h^2=\left(\sqrt{5} \right)^2[/tex]
[tex]\qquad z^2+\left(\dfrac{4}{\sqrt{5}} \right)^2 \stackrel{\textcolor{#800000}{(iv)}}{=} 5[/tex]
[tex]\qquad z^2+\dfrac{16}{5}= 5[/tex]
[tex]\qquad z^2= 5-\dfrac{16}{5}=\dfrac{9}{5}[/tex]
e, como [tex]z \gt 0[/tex], já que [tex]z[/tex] é o comprimento de um dos lados de um triângulo, temos que [tex]\boxed{z= \dfrac{3}{\sqrt{5}}}. \, \quad \textcolor{#800000}{(v)}[/tex]
Por [tex]\textcolor{#800000}{(iv)}[/tex] e [tex]\textcolor{#800000}{(v)} \, [/tex], segue que
[tex]\qquad S_1=\dfrac{z \cdot h}{2}=\dfrac{\dfrac{3}{\sqrt{5}} \cdot \dfrac{4}{\sqrt{5}}}{2}=\dfrac{\dfrac{12}{5}}{2}=\dfrac{12}{10}[/tex]
e, então, [tex]\boxed{S_1=\dfrac{6}{5} \, \text{cm}^2} \, \quad \textcolor{#800000}{(vi)}[/tex]
Finalmente, por [tex]\textcolor{#800000}{(ii)} \, [/tex], [tex]\textcolor{#800000}{(iii)}[/tex] e [tex]\textcolor{#800000}{(vi)} \, [/tex], segue que:
[tex]\qquad S=\dfrac{6}{5}+1=\dfrac{6+5}{5}=\dfrac{11}{5}[/tex]
e, portanto, a área do quadrilátero [tex]BCFE[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{11}{5} \, \text{cm}^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
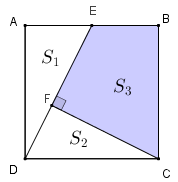
Observe, inicialmente, que a área [tex]S[/tex] do quadrado [tex]ABCD[/tex] é a soma das áreas dos triângulos [tex]EAD[/tex] e [tex]FCD[/tex] e do quadrilátero [tex]BCFE \, [/tex], conforme podemos observar na figura ao lado.
Assim, [tex]\boxed{S_1+S_2+S_3=4 \, \text{cm}^2}. \quad \textcolor{#800000}{(i)}[/tex]
Perceba que [tex]S_3[/tex] é a área pedida no problema, então precisamos calcular as áreas [tex]S_1[/tex] e [tex]S_2.[/tex]
- Área [tex]S_1[/tex]
Como [tex]EAD[/tex] é um triângulo retângulo de catetos medindo [tex]1[/tex] e [tex]2[/tex] centímetros, a área [tex]S_1[/tex] é dada por:
[tex]\qquad \boxed{S_1= \dfrac{1\times 2}{2}=1 \, \text{cm}^2} \, \quad \textcolor{#800000}{(ii)}[/tex].
- Área [tex]S_2[/tex]
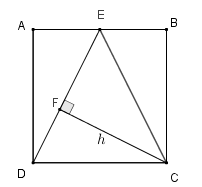
Aqui teremos um pouco mais de trabalho, pois precisaremos calcular os comprimentos dos segmentos [tex]CF[/tex] e [tex]FD.[/tex] Vamos lá… - Para calcularmos o comprimento [tex]h[/tex] do segmento [tex]CF \, [/tex], observamos na figura ao lado que a área do triângulo [tex]EDC[/tex] é [tex]\dfrac{2\times 2}{2}=2 \, \text{cm}^2[/tex] e que essa área pode também ser calculada utilizando-se como base o segmento [tex]ED[/tex] e como altura o segmento [tex]CF.[/tex]
Observe que, utilizando o Teorema de Pitágoras, podemos obter facilmente o comprimento do segmento [tex]ED[/tex], uma vez que se esse comprimento for [tex]x \, \text{cm}[/tex], então [tex]x^2=2^2+1^2=5[/tex] e, com isso, temos que [tex]\boxed{x=\sqrt{5} \, \text{cm}} \, . \quad \textcolor{#800000}{(iii)}[/tex]
Dessa forma, segue que:
[tex]\qquad 2= \dfrac{base \times altura}{2}= \dfrac{x \times h}{2} \stackrel{\textcolor{#800000}{(iii)}}{=} \dfrac{\sqrt{5} \times h}{2}[/tex]
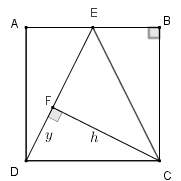
donde concluímos que [tex]\boxed{h= \dfrac{4}{\sqrt{5}} \, \text{cm}}. [/tex] - Para calcularmos o comprimento [tex]y[/tex] do segmento [tex]FD \, [/tex], observamos na figura ao lado que [tex]DFC[/tex] é um triângulo retângulo. Assim, utilizando o Teorema de Pitágoras, temos que:
[tex]\qquad y^2+h^2=4[/tex]
[tex]\qquad y^2+\left( \dfrac{4}{\sqrt{5}} \right)^2=4[/tex]
[tex]\qquad y^2+\dfrac{16}{5} =4[/tex]
[tex]\qquad y^2=4-\dfrac{16}{5}[/tex]
[tex]\qquad y^2=\dfrac{4}{5}[/tex]
e, sendo [tex]y \gt 0[/tex], concluímos que [tex]\boxed{y=\dfrac{2}{\sqrt{5}} \, \text{cm}}. [/tex]
Pronto, já podemos calcular a área [tex]S_2[/tex]:
[tex]\qquad S_2=\dfrac{base \times altura}{2}=\dfrac{y\times h}{2}=\dfrac{\dfrac{2}{\sqrt{5}}\times \dfrac{4}{\sqrt{5}}}{2}[/tex]
ou seja, [tex]\boxed{S_2= \dfrac{4}{5} \, \text{cm}^2}. \, \quad \textcolor{#800000}{(iv)}[/tex]
Finalmente, por [tex]\textcolor{#800000}{(i)} \, [/tex], [tex]\textcolor{#800000}{(ii)}[/tex] e [tex]\textcolor{#800000}{(iv)} \, [/tex], segue que
[tex]\qquad S_1+S_2+S_3=4[/tex]
[tex]\qquad S_3=4-S_1-S_2[/tex]
[tex]\qquad S_3=4-1-\dfrac{4}{5}[/tex]
[tex]\qquad S_3=3-\dfrac{4}{5}[/tex]
[tex]\qquad S_3=\dfrac{15-4}{5}[/tex]
[tex]\qquad S_3=\dfrac{11}{5}.[/tex]
Portanto, a área do quadrilátero [tex]BCFE[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{11}{5} \, \text{cm}^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Ferramentas que podem ajudar na próxima solução
Solução 3

Esta solução começa como a anterior, observando que a área [tex]S[/tex] do quadrado [tex]ABCD[/tex] é a soma das áreas dos triângulos [tex]EAD[/tex] e [tex]FCD[/tex] e do quadrilátero [tex]BCFE \, [/tex], conforme podemos observar na figura ao lado. Assim, [tex]\boxed{S_1+S_2+S_3=4 \, \text{cm}^2} \quad \textcolor{#800000}{(i)}[/tex].
Perceba que [tex]S_3[/tex] é a área pedida no problema, então precisamos calcular as áreas [tex]S_1[/tex] e [tex]S_2.[/tex]
A área [tex]S_1[/tex] é imediata pois, como [tex]EAD[/tex] é um triângulo retângulo de catetos medindo [tex]1[/tex] e [tex]2[/tex] centímetros, temos:
[tex]\qquad \boxed{S_1= \dfrac{1\times 2}{2}=1 \, \text{cm}^2} \, \quad \textcolor{#800000}{(ii)}[/tex].
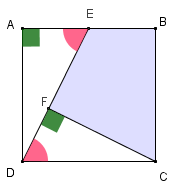
Para prosseguir, vamos utilizar a semelhança entre os triângulos [tex]AED[/tex] e [tex]FDC[/tex].
De fato, note que os ângulos [tex]FDC \, [/tex]e [tex] \, AED[/tex] são congruentes, pois são ângulos alternos internos definidos por duas paralelas e uma transversal. Logo, pelo caso [tex]A.A.[/tex], os triângulos [tex]AED[/tex] e [tex]FDC[/tex] são semelhantes (ver figura ao lado).
Veja que a razão de semelhança pode ser obtida pela razão entre os comprimentos das hipotenusas dos triângulos [tex]AED[/tex] e [tex]FDC[/tex], digamos [tex]a \, [/tex] e [tex] \, f[/tex], respectivamente:
[tex]\qquad \dfrac{a}{f}=\boxed{\dfrac{a}{2}} \, \quad \textcolor{#800000}{(iii)}[/tex]
e podemos calcular o comprimento [tex]a \, [/tex] do segmento [tex]DE[/tex] aplicando o Teorema de Pitágoras ao triângulo [tex]AED[/tex], já que conhecemos os comprimentos dos catetos [tex]\overline{AE}[/tex] e [tex]\overline{AD} \, [/tex], respectivamente [tex]1 \, \text{cm}[/tex] e [tex]2 \, \text{cm}[/tex]:
[tex]\qquad a^2=1^2+2^2=5[/tex], donde [tex]\boxed{DE=\sqrt5 \, \text{cm}} \, \quad \textcolor{#800000}{(iv)}[/tex].
Por [tex]\textcolor{#800000}{(iii)}[/tex] e [tex]\textcolor{#800000}{(iv)}[/tex], a razão de semelhança entre os triângulos [tex]AED[/tex] e [tex]FDC[/tex] é dada por [tex]\dfrac{DE}{2}=\boxed{\dfrac{\sqrt5}{2}}[/tex]. Logo, a razão entre as áreas desses triângulos será [tex]\dfrac{S_1}{S_2}=\left(\dfrac{\sqrt5}{2}\right)^2=\dfrac{5}{4}[/tex], isto é, teremos [tex]S_2=\dfrac{4}{5}S_1=\dfrac{4}{5}\times 1=\boxed{\dfrac{4}{5} \, \text{cm}^2} \, \quad \textcolor{#800000}{(v)}[/tex].
Finalmente, por [tex]\textcolor{#800000}{(i)} \, [/tex], [tex]\textcolor{#800000}{(ii)}[/tex] e [tex]\textcolor{#800000}{(v)} \, [/tex], segue que:
[tex]\qquad S_1+S_2+S_3=4[/tex]
[tex]\qquad S_3=4-S_1-S_2[/tex]
[tex]\qquad S_3=4-1-\dfrac{4}{5}[/tex]
[tex]\qquad S_3=3-\dfrac{4}{5}[/tex]
[tex]\qquad S_3=\dfrac{15-4}{5}[/tex]
[tex]\qquad S_3=\dfrac{11}{5}.[/tex]
Portanto, a área do quadrilátero [tex]BCFE[/tex] é [tex] \, \fcolorbox{black}{#eee0e5}{$\dfrac{11}{5} \, \text{cm}^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
