✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
Para presentear sua avó, Aninha pintou um quadro com bonequinhas coloridas de tamanhos diferentes, de forma que, a partir da primeira, a altura de cada uma corresponde a 3/4 da altura da bonequinha anterior.
Se a maior delas tem 16 cm de altura, qual é o número natural que melhor aproxima a altura, em milímetros, da bonequinha menor?
A figura não está em escala
Solução 1
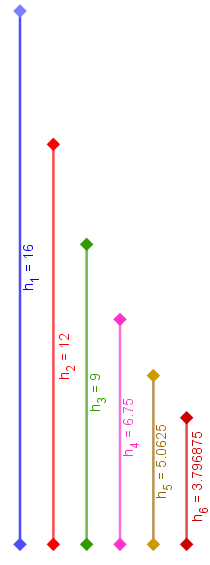
Como no quadro que Aninha pintou aparecem apenas seis bonequinhas, podemos fazer as contas diretamente, sem utilizar nenhum artifício:
[tex]\begin{array}{|l|l|}
\hline
\text{Bonequinha 1}& h_1=16 \, cm\\
\hline
\text{Bonequinha 2}& h_2=h_1\times \dfrac{3}{4}=12 \, cm\\
\hline
\text{Bonequinha 3}& h_3=h_2\times \dfrac{3}{4}=9 \, cm\\
\hline
\text{Bonequinha 4}& h_4=h_3\times \dfrac{3}{4}=6,75 \, cm\\
\hline
\text{Bonequinha 5}& h_5=h_4\times \dfrac{3}{4}=5,0625 \, cm\\
\hline
\text{Bonequinha 6}& h_6=h_5 \times \dfrac{3}{4}=3,796875 \, cm\\
\hline
\end{array}[/tex]
A figura ao lado mostra a variação em centímetros das alturas das bonequinhas.
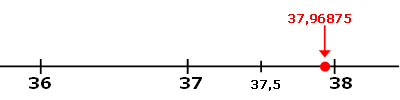
Pelos nossos cálculos a altura da sexta bonequinha é [tex]3,796875 \, [/tex] centímetros ou, de forma equivalente, [tex]37,96875 \, [/tex] milímetros.
Assim, o número natural que melhor aproxima a altura, em milímetros, da bonequinha menor é [tex]\fcolorbox{black}{#eee0e5}{$38$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Poderíamos ter resolvido algebricamente este problema, tentando estabelecer um padrão para a variação das alturas das bonequinhas. Se não fizéssemos as continhas indicadas na tabela, poderíamos observar a sequência algébrica das alturas e estabelecer esse padrão. Observe.
[tex]\begin{array}{|l|l|}
\hline
\text{Bonequinha 1}& h_1=16 \, cm\\
\hline
\text{Bonequinha 2}& h_2=16\times \dfrac{3}{4}\\
\hline
\text{Bonequinha 3}& h_3=\left(16\times \dfrac{3}{4}\right)\times \dfrac{3}{4}=16\times\left(\dfrac{3}{4}\right)^2=16\times \dfrac{3^2}{4^2}\\
\hline
\text{Bonequinha 4}& h_4=\left(16\times\left(\dfrac{3}{4}\right)^2\right)\times \dfrac{3}{4}=16\times\left(\dfrac{3}{4}\right)^3=16\times \dfrac{3^3}{4^3}\\
\hline
\text{Bonequinha 5}& h_5=\left(16\times\left(\dfrac{3}{4}\right)^3\right)\times \dfrac{3}{4}=16\times\left(\dfrac{3}{4}\right)^4=16\times \dfrac{3^4}{4^4}\\
\hline
\qquad \vdots &\qquad \qquad \vdots \\
\hline
\text{Bonequinha n,} \\
\text{com }n \gt 2 & h_n=\left(16\times\left(\dfrac{3}{4}\right)^{n-2}\right)\times \dfrac{3}{4}=16\times\left(\dfrac{3}{4}\right)^{n-1}=16\times \dfrac{3^{n-1}}{4^{n-1}}\\
\hline
\end{array}[/tex]
A vantagem desse método, não é observada para [tex]n=6[/tex], pois a próxima linha da segunda tabela nos daria a altura correspondente. Mas observe que, usando o padrão, podemos facilmente perceber, por exemplo, que a altura de uma suposta vigésima bonequinha seria dada pelo padrão [tex] \boxed{h_n=16\times\left(\dfrac{3}{4}\right)^{n-1}=16\times \dfrac{3^{n-1}}{4^{n-1}}}[/tex], quando [tex]n=20[/tex]: [tex]\boxed{h_{20}=16\times\left(\dfrac{3}{4}\right)^{19}=16\times \dfrac{3^{19}}{4^{19}}}\, .[/tex]
É claro que dependeríamos de uma calculadora para efetuarmos as contas indicadas e obtermos:
[tex]\qquad h_{20}\approx 0,06765 \, cm=0,6765 \, mm \,.[/tex]
(Nem enxergaríamos a bonequinha, mas saberíamos a sua altura!!!!)
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |