Problema
(Indicado a partir do 2º ano do E. M.)
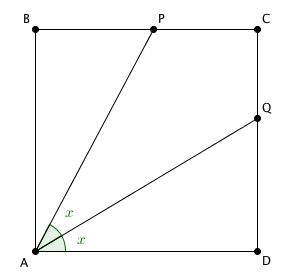
Na figura abaixo, [tex]ABCD[/tex] é um quadrado.
Sabendo que [tex]BP = 8\,cm[/tex] e que [tex]QD = 9\,cm[/tex], calcule a medida de [tex]\overline{PQ}[/tex].

Lembretes
1) Para valores reais de [tex]x[/tex] tais que [tex]\begin{cases}
x\ne \frac{\pi}{2}+k\pi,\forall k \in \mathbb{Z}\\
x\ne \frac{\pi}{4}+k\frac{\pi}{2},\forall k \in \mathbb{Z}
\end{cases}[/tex] é válida a seguinte identidade trigonométrica:
[tex]\qquad \qquad tg(2x)=\dfrac{2\, tg(x)}{1-tg^2(x)}.[/tex] (tangente do arco duplo)
2) Ângulos alternos internos definidos por duas paralelas e uma transversal são congruentes! Se você não se lembra do assunto, não deixe de dar uma passadinha nesta Sala para Leitura.
Solução
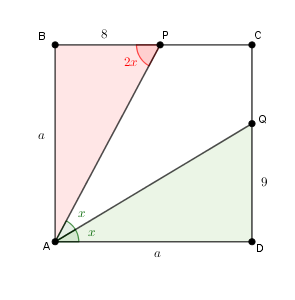
- Perceba que temos [tex]B\hat{P}A = 2x[/tex], pois [tex]B\hat{P}A[/tex] e [tex]P\hat{A}D[/tex] são alternos internos definidos por duas paralelas e uma transversal sendo, portanto, congruentes.
- Seja [tex]a[/tex] a medida do lado do quadrado.
Como [tex] tg\, \theta=\dfrac{\text{cateto oposto a } \theta}{\text{cateto adjacente a } \theta} \, [/tex], nos triângulos retângulos [tex]BPA[/tex] e [tex]AQD[/tex], obtemos [tex] \, \boxed{tg(2x) = \dfrac{a}{8}} \, [/tex] e [tex] \, \boxed{tg(x)= \dfrac{9}{a}} \, [/tex], respectivamente.
Agora, utilizando a relação da tangente do arco duplo, segue que:
[tex]\quad tg(2x)=\dfrac{2\, tg(x)}{1-tg^2(x)}[/tex]
[tex]\quad \dfrac{a}{8}=\dfrac{2\cdot\frac{9}{a}}{1-(\frac{9}{a})^2}[/tex]
[tex]\quad \dfrac{a}{8}=\dfrac{\frac{18}{a}}{1-\frac{81}{a^2}}[/tex]
[tex]\quad \dfrac{a}{8}\cdot \left(1-\dfrac{81}{a^2}\right)=\dfrac{18}{a}[/tex]
[tex]\quad \dfrac{a}{8}-\dfrac{81}{8a}=\dfrac{18}{a}[/tex] (multiplicando por [tex]8a[/tex])
[tex]\quad a^2-81=144[/tex]
[tex]\quad a^2=225[/tex]
[tex]\quad a=15[/tex] (escolhemos a raiz positiva porque [tex]a[/tex] é uma medida).
Portanto, [tex]PC = 15-8=7\,cm \, [/tex] e [tex] \, CQ = 15-9=6\,cm[/tex].
Finalmente, aplicando o teorema de Pitágoras no triângulo [tex]PCQ[/tex], temos [tex]\fcolorbox{black}{#eee0e5}{$PQ = \sqrt{7^2+6^2}=\sqrt{85}\,cm$} \, [/tex].
Solução elaborada pelos Moderadores do Blog.
