✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
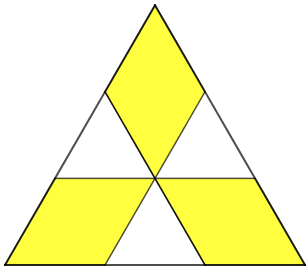
A partir de um grande triângulo equilátero com área de [tex]9 \, cm^2[/tex], Aline fez o desenho mostrado na figura.
Os segmentos de reta internos que ela desenhou são paralelos aos lados do triângulo maior e dividem cada um desses lados em três partes iguais.
Qual a área da parte colorida de amarelo?
Ferramentas que podem ajudar
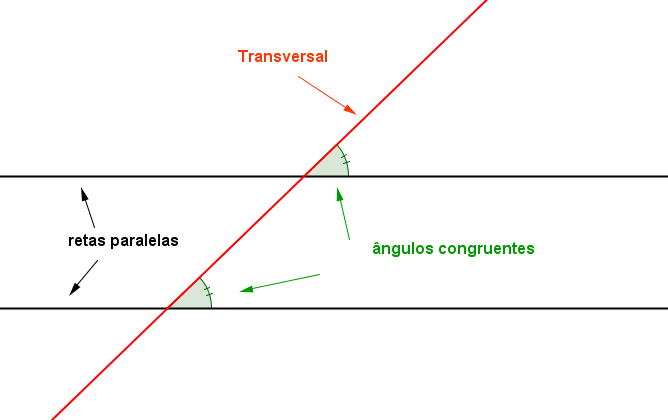
Reta transversal a outras retas é uma reta que intersecta essas outras retas em pontos diferentes.
Solução 1
Observe a figura abaixo.
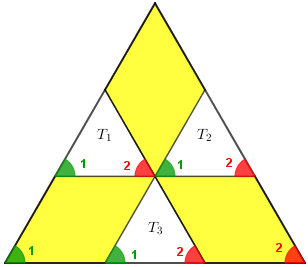
- Perceba que, por múltiplas aplicações da Propriedade 1, podemos concluir que todos os ângulos indicados por 1 têm a mesma medida, assim como os indicados com 2.
Essa observação sobre a congruência dos ângulos destacados na figura nos dá uma primeira informação importante para resolvermos o problema:
- pela Propriedade 2, os triângulos [tex]T_1 \, [/tex], [tex]T_2 \, [/tex], [tex]T_3[/tex] e o original são semelhantes.
(Na verdade, como o triângulo original é equilátero, todas as medidas dos ângulos desses quatro triângulos são iguais, ou seja, os ângulos indicados por 1 e por 2 são congruentes.)
Como os lados do triângulo maior foram divididos em três partes iguais, a razão de semelhança entre o triângulo maior e cada um dos triângulos [tex]T_1 \, [/tex], [tex]T_2 \, [/tex] e [tex]T_3[/tex] é [tex]3[/tex]. Assim, pela Propriedade 3, a área do triângulo maior é nove vezes maior do que a área de cada um desses triângulos pequenos.
Dessa forma, [tex]T_1 \, [/tex], [tex]T_2 \, [/tex] e [tex]T_3[/tex] têm área [tex]\boxed{\dfrac{9}{9}=1 \, cm^2} \, [/tex] cada um.
Por outro lado, observe que a área da região colorida de amarelo é a área do triângulo externo menos a área desses triângulos. Assim, a área da região colorida de amarelo, [tex]A_a \, [/tex], é dada por:
[tex]\qquad A_a=9-3 \times 1=9-3=\fcolorbox{black}{#FFFF00}{$6 \, cm^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Observe que os segmentos tracejados definem nove triângulos internos ao triângulo maior da figura original.
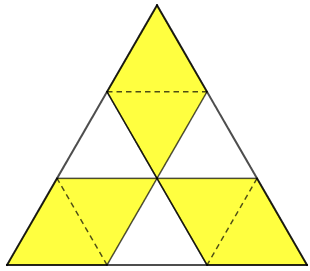
- Perceba que as alturas dos triângulos menores têm o mesmo comprimento, pois estão em perpendiculares a retas paralelas que se encontram a uma mesma distância, já que os lados do triângulo maior foram divididos em partes com o mesmo comprimento.
- As bases dos triângulos menores têm o mesmo comprimento, pois estão em retas paralelas e são limitadas por outras paralelas que se encontram a uma mesma distância.
Assim, os nove triângulos internos ao triângulo maior têm a mesma área e, portanto, cada um tem área de [tex]\dfrac{9}{9}=1\,cm^2.[/tex]
Finalizando, a parte colorida de amarelo é formada por seis desses triângulos internos; assim, sua área é dada por:
[tex]\qquad A_a=6 \times 1=\fcolorbox{black}{#FFFF00}{$6 \, cm^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
