Jogos matemáticos e a Teoria dos Jogos
A Teoria dos jogos é um ramo da matemática aplicada que estuda situações estratégicas onde jogadores escolhem diferentes ações na tentativa de melhorar seu retorno. Inicialmente desenvolvida como ferramenta para compreender comportamento econômico e depois usada pela Corporação RAND para definir estratégias nucleares, a teoria dos jogos é hoje usada em diversos campos acadêmicos. A partir de [tex]1970[/tex], a teoria dos jogos passou a ser aplicada ao estudo do comportamento animal, incluindo evolução das espécies por seleção natural. Devido a interesse em jogos como o dilema do prisioneiro iterado, no qual interesses próprios e racionais prejudicam a todos, a teoria dos jogos vem sendo aplicada nas ciências políticas, ciências militares, ética, economia, filosofia, recentemente, no jornalismo, área que apresenta inúmeros e diversos jogos, tanto competitivos como cooperativos. Finalmente, a teoria dos jogos despertou a atenção da ciência da computação que a vem utilizando em avanços na inteligência artificial e cibernética.
A teoria dos jogos tornou-se um ramo proeminente da matemática nos anos [tex]30[/tex] do século [tex]XX[/tex], especialmente depois da publicação em [tex]1944[/tex] de The Theory of Games and Economic Behavior de John von Neumann e Oskar Morgenstern. A teoria dos jogos distingue-se na economia na medida em que procura encontrar estratégias racionais em situações em que o resultado depende não só da estratégia própria de um agente e das condições de mercado, mas também das estratégias escolhidas por outros agentes que possivelmente têm estratégias diferentes ou objetivos comuns.
Os resultados da teoria dos jogos tanto podem ser aplicados a simples jogos de entretenimento como a aspectos significativos da vida em sociedade. Um exemplo deste último tipo de aplicações é o Dilema do prisioneiro (esse jogo teve sua primeira análise no ano de [tex]1953[/tex]) popularizado pelo matemático Albert W. Tucker, e que tem muitas implicações no estudo da cooperação entre indivíduos. Os biólogos utilizam a teoria dos jogos para compreender e prever o desfecho da evolução de certas espécies. Esta aplicação da teoria dos jogos à teoria da evolução produziu conceitos tão importantes como o conceito de Estratégia Evolucionariamente Estável, introduzida pelo biólogo John Maynard Smith no seu ensaio Game Theory and the Evolution of Fighting.Na economia, a teoria dos jogos tem sido usada, segundo Joseph Lampel, para examinar a concorrência e a cooperação dentro de pequenos grupos de empresas. A partir daí, era apenas um pequeno passo até a estratégia. Pesquisadores de administração de estratégia têm procurado tirar proveito da teoria dos jogos, pois ela provê critérios valiosos quando lida com situações que permitem perguntas simples, não fornecendo respostas positivas ou negativas, mas ajuda a examinar de forma sistemática várias permutações e combinações de condições que podem alterar a situação. As questões estratégicas da vida real dão origem a um número imenso de variações, impossibilitando o tratamento exaustivo de todas as possibilidades. Assim o objetivo não é resolver as questões estratégicas, mas sim ajudar a ordenar o pensamento estratégico – provendo um conjunto de conceitos para a compreensão das manobras dinâmicas contra os concorrentes.
Em complemento ao interesse acadêmico, a teoria dos jogos vem recebendo atenção da cultura popular. Um pesquisador da Teoria dos Jogos e ganhador do Prémio de Ciências Econômicas em Memória de Alfred Nobel, John Nash, foi sujeito, em [tex]1998[/tex], de biografia por Sylvia Nasar e de um filme em [tex]2001[/tex] Uma mente brilhante, vale a pena assistir, em minha opinião um dos melhores do gênero, com estímulo à matemática e ao estudo. A teoria dos Jogos também foi tema em [tex]1983[/tex] do filme Jogos de Guerra. Embora similar à teoria da decisão, a teoria dos jogos estuda decisões que são tomadas em um ambiente onde vários jogadores interagem. Em outras palavras, a teoria dos jogos estuda as escolhas de comportamentos ótimos quando o custo e benefício de cada opção não é fixo, mas depende, sobretudo, da escolha dos outros indivíduos.
Como quando crianças, ficamos entusiasmados com problemas como jogo da velha, entre vários outros. Da curiosidade natural de entendê-los surge a Teoria dos Jogos, a análise matemática de tais situações, fruto primeiro da pura curiosidade matemática.
Teoria dos Jogos é isso: entender que sua decisão não é independente e ambos os ganhos dependem da combinação de muitas ações em cadeia até chegar em um equilíbrio. Este equilíbrio é o chamado Equilíbrio de Nash, em homenagem a John Nash Jr, prêmio Nobel de 1994 e que foi personagem de Russell Crowe no filme Uma Mente Brilhante, ganhador do Oscar de [tex]2002[/tex].
Assim como várias teorias de administração ajudam a estruturar o seu pensamento nas decisões competitivas, a Teoria dos Jogos possui modelos formais e exemplos que facilitam o entendimento nas decisões interdependentes, além de facilitar a comunicação e treinamento dos conceitos como qualquer teoria formal. A base da teoria é colocar-se na posição do outro e raciocinar o que você faria em cada situação, modelando todas as interações com benefícios/prejuízos de ambos e daí tomar a melhor ação estratégica.
A Teoria dos Jogos, como disciplina independente, não resolve todos os problemas, mas apresenta vários insights para melhorar seu pensamento estratégico como um elemento complementar das demais Teorias de Decisões. Para se aprofundar e para ser um bom estrategista, é importante unir os conceitos das disciplinas de Estratégia, da Economia Clássica (como preferências e utilidades, resultado esperado, risco e incerteza, free-rider, assimetria de informações) e da Teoria Comportamental (heurísticas e vieses cognitivos). Neste último caso, quanto mais você souber quais são os incentivos e reais motivações do seu concorrente ou parceiro, maiores as suas chances de ganhar o jogo. A união de todos os elementos é uma grande forma para melhorar suas decisões estratégicas.
Um pouco mais de Teoria dos Jogos
A teoria dos jogos tem a finalidade de prever os movimentos dos outros jogadores, sejam eles concorrentes ou aliados, através dessa teoria os jogadores se posicionam da melhor forma para obter o resultado desejado. O objetivo da teoria dos jogos é entender a lógica na hora da decisão e ajudar a responder se é possível haver colaboração entre os jogadores, em quais circunstâncias o mais racional é não colaborar e quais estratégias devem ser adotadas para garantir a colaboração entre os jogadores. A teoria dos jogos, por meio da matemática, equaciona os conflitos, onde o foco são as estratégias utilizadas pelos jogadores.
Cena do Filme
Uma mente brilhante
As Origens da teoria dos Jogos – Um pouco de História
Devido à falta de interesse científico, até [tex]1920[/tex], não haviam análises técnicas adequadas para estudar estratégias de jogos. Os jogos de tabuleiros, dados, cartas, ou em geral, os jogos de salão, divertem a humanidade desde a formação das primeiras civilizações, por colocarem as pessoas em situações nas quais vencer ou perder dependem das escolhas feitas no início das partidas, sendo assim, o jogo se tornou uma ferramenta para o desenvolvimento das
pessoas, mas só despertou interesse após muito tempo, com o surgimento da teoria da probabilidade.
Os estudos sobre a teoria da probabilidade tiveram início com o filósofo, matemático e físico francês Blaise Pascal, juntamente com o matemático francês Fermat, através desses estudos desenvolveram a teoria da probabilidade em jogos de azar utilizando regras matemáticas. Em seguida Antoine Augustin Cournot ([tex]1801-1877[/tex]), matemático francês, com estudo da análise do ponto de equilíbrio nas estratégias de jogos, formalizou um conceito especifico de equilíbrio, ou seja, aplicados em casos particulares, que mais tarde foi generalizado por John Forbes Nash Jr. Mas o marco inicial da teoria dos jogos foi quando John Von Neumann ([tex]1903-
1957[/tex]), matemático húngaro-americano, provou o teorema minimax, segundo este teorema há sempre uma solução racional para um conflito bem definido entre dois indivíduos cujos interesses são completamente opostos, teorema deixado aberto pelo matemático francês Émile Borel ([tex]1871-1956[/tex]).
A solução foi publicada no artigo Zur Theorie der Gesellschaftsspiele (Sobre a Teoria dos Jogos de Estratégia, [tex]1928[/tex]), nesse período Oskar Morgenstern ([tex]1902-1977[/tex]), economista alemão, estava por publicar o livro Implicações Quantitativas do comportamento do Máximo, no qual discute qual deveria ser a unidade de análise econômica: o individualismo ou a interação social. Chegando à conclusão que os indivíduos interagem, então a sua racionalidade é relativa, se a racionalidade do indivíduo não é plena então a sua maximização também não será. A obra de Morgenstern expõe que o máximo depende diretamente da interação entre os indivíduos e indiretamente do meio no qual os indivíduos interagem. Por isso Morgenstern e Von Neumann juntaram os seus trabalhos e publicaram, em [tex]1944[/tex], a obra: The Theory of Games and Economics Behavior (Teoria dos Jogos e Comportamento Econômico, [tex]1944[/tex]), que além de desenvolver uma teoria de jogos para mais participantes afirmam que o comportamento da economia depende, fundamentalmente, da interação entre os agentes, já que ele afeta diretamente a elaboração de estratégias e tomadas de decisão dos produtores e dos consumidores.
Neste período começou a utilização das primeiras ideias sobre teoria dos jogos, cientificamente, com a finalidade de descobrir a melhor forma de jogar onde os participantes dependiam de habilidade e de sorte (jogos de azar), sendo a teoria dos jogos passada a ser uma ferramenta da matemática aplicada. Em ataque a proposição de Von Neumann de procurar a melhor jogada, Borel publica a obra: Aplicações para jogos da Sorte, onde discute a determinação da estratégia mista, pois Borel desiste de procurar a fórmula perfeita para jogos, segundo ele, as jogadas ótimas são difíceis de serem descobertas em jogos reais e, mesmo se encontrada as pessoas deixariam de jogar. Em [tex]1950[/tex], John Forbes Nash Junior, matemático estadunidense que conquistou o prêmio Nobel de economia em 1994, um dos principais nomes da história da Teoria dos Jogos, formado pela Universidade de Princeton, em [tex]1950[/tex], com a tese NonCooperative Games (Jogos Não-Cooperativos, publicada em [tex]1951[/tex]) que lhe valeu mais tarde a indicação para o Nobel. Nesta tese, Nash provou a existência de ao menos um ponto de equilíbrio em jogos de estratégias para múltiplos jogadores, mas para que ocorra o equilíbrio é necessário que os jogadores se comportem racionalmente e não se comuniquem antes do jogo para evitar acordos.
Em princípio o equilíbrio de Nash era utilizado para jogos de informação completa, mas, com trabalhos posteriores de Harsanyi e Selten, o mesmo passou a ser aplicado, também, em jogos de informação incompleta, a principal contribuição desses autores foi mostrar que a teoria dos jogos de informação completa pode ser estendida para cobrir certas situações importantes nas quais a informação é incompleta. A partir desses trabalhos começaram a surgir novas técnicas de solução de jogos e a serem aplicadas em diferentes áreas de estudo, como economia, biologia e ciências políticas. Nash não fez a Teoria dos jogos, mas modificou-a, pois Neumann utilizava suas teses para trabalho unitário, já Nash fez seu trabalho valer em grupo, modificando a economia mundial, hoje muitas pessoas utilizam seus estudos e nem sabem que ele ainda é vivo, ministra aulas e é ganhador do Prêmio Nobel de Economia por não haver prêmio Nobel em Matemática.
Cena do filme
Uma mente brilhante
Entre 1949 e 1953, além deste trabalho, escreveu mais artigos ligados à teoria dos jogos o chamado programa de Nash para solução de jogos estratégicos: The Bargaining Problem (O Problema da Barganha, [tex]1949[/tex]); Equilibrium Points in N-Person Games (Pontos de Equilíbrio em Jogos de N-Pessoas, [tex]1950[/tex]) e Two-Person Cooperative Games (Jogos Cooperativos de Duas Pessoas, [tex]1953[/tex]). Também escreveu artigos de matemática pura sobre variedades algébricas, em [tex]1951[/tex] e de arquitetura de computadores, em [tex]1954[/tex]. Contudo, Nash tinha problemas de esquizofrenia que se agravou ao extremo, afastou-se das pesquisas e submeteu-se a um tratamento rigoroso durante alguns anos. Depois da estabilização do seu quadro mental volta a ministrar aulas no departamento de matemática de Princeton. Em dezembro de [tex]1994[/tex], recebe a medalha com a efígie de Alfred Nobel, das mãos do rei da Suécia. Sua vida conturbada foi tema de biografia escrita por Sylvia Nasar que originou o filme Uma Mente Brilhante, que recebeu o Oscar de [tex]2001[/tex], como já dito anteriormente.
Curiosidade: um pouco sobre o jogo HEX
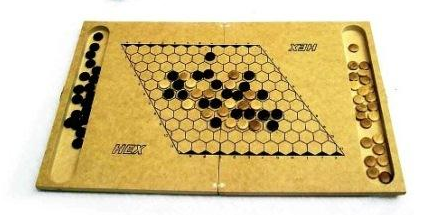
Cada jogador tem uma cor, vermelho e azul ou branco e preto sendo convencionais. Os jogadores se revezam colocando uma pedra da sua cor em uma única célula dentro do tabuleiro global de jogo. O objetivo é formar um caminho conectado de suas pedras que liga os lados opostos do tabuleiro marcados com suas cores, antes de seu oponente conecte os seus lados de forma semelhante. O primeiro jogador a completar a sua ligação ganha o jogo. Os quatro cantos de cada hexágono das bordas pertencem a ambos os lados adjacentes.
Uma vez que o primeiro jogador a se mover em Hex tem uma vantagem distinta, a regra da torta geralmente é implementada por justiça. Esta regra permite que o segundo jogador escolha se quer trocar de posições com o primeiro jogador após o primeiro jogador fazer o primeiro movimento.
Roger Leite Lucena
aluno do PIC – OBMEP
Para saber um pouco mais:
[tex]\bullet\, \, [/tex] [1] Teoria dos jogos
[tex]\bullet\, \, [/tex] [2] Jogos no Ensino da Matemática