✏ Link do problema para dispositivos da Apple.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Difícil)
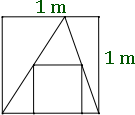
Aninha inscreveu um quadrado em um triângulo que, por sua vez, está inscrito em um outro quadrado com [tex]1[/tex] metro de lado.
Qual é a área, em metros quadrados, do quadrado menor?
Solução
Observe, inicialmente, que a área do triângulo inscrito no quadrado maior é [tex]\dfrac{1}{2}.[/tex]
Observe, também, que a área desse triângulo é a soma das áreas do quadrado menor e de três triângulos menores, conforme vemos na figura abaixo.
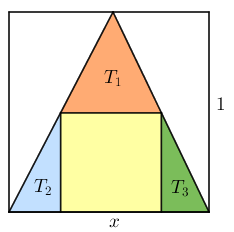Assim, se:
- [tex]x[/tex] é comprimento dos lados do quadrado menor;
- [tex]A_q[/tex] é a área do quadrado menor;
- [tex]A_1[/tex] é a área do triângulo [tex]T_1[/tex];
- [tex]A_2[/tex] é a área do triângulo [tex]T_2[/tex];
- [tex]A_3[/tex] é a área do triângulo [tex]T_3[/tex];
então podemos afirmar que:
[tex]\qquad\dfrac{1}{2}=A_q+A_1+A_2+A_3[/tex]
[tex]\qquad\dfrac{1}{2}=x^2+\dfrac{x(1-x)}{2}+A_2+A_3. \qquad \textcolor{#800000}{(i)}[/tex]
Não sabemos quais são os comprimentos das bases dos triângulos [tex]T_2[/tex] e [tex]T_3[/tex], mas observamos que a soma desses comprimentos é [tex]1-x[/tex] e a altura relativa a essa base de cada um é [tex]x[/tex]. Com isso, temos que [tex]A_2+A_3=\dfrac{x(1-x)}{2}[/tex] e, portanto, segue por [tex] \textcolor{#800000}{(i)}[/tex] que:
[tex]\qquad\dfrac{1}{2}=x^2+\dfrac{x(1-x)}{2}+\left(A_2+A_3\right)[/tex]
[tex]\qquad\dfrac{1}{2}=x^2+\dfrac{x(1-x)}{2}+\dfrac{x(1-x)}{2}[/tex]
[tex]\qquad\dfrac{1}{2}=x^2+2 \, \dfrac{x(1-x)}{2}[/tex]
[tex]\qquad\dfrac{1}{2}=x^2+\cancel{2} \, \dfrac{x(1-x)}{\cancel{2}}[/tex]
[tex]\qquad\dfrac{1}{2}=x^2+x(1-x)[/tex]
[tex]\qquad\dfrac{1}{2}=x^2+x-x^2[/tex]
[tex]\qquad \boxed{x=\dfrac{1}{2}}.[/tex]
Como o lado do quadrado menor é [tex]\dfrac{1}{2} \, m[/tex], então sua área é [tex]\left(\dfrac{1}{2}\right)^2=\fcolorbox{black}{#eee0e5}{$\dfrac{1}{4} \, m^2$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Um applet para ajudar. . .
Você pode utilizar este applet para observar duas propriedades que aparecem implicitamente na solução deste problema:
- A medida dos lados do quadrado interno não se altera ao modificarmos a forma do triângulo.
- O comprimento dos lados do quadrado menor é a metade do comprimento dos lados do quadrado maior.
Instruções:
1) Aguarde o aplicativo carregar completamente.
2) Para modificar a forma do triângulo inscrito, clique sobre o ponto P e, mantendo o mouse pressionado, movimente-o.
3) Para modificar a medida do quadrado externo, clique sobre o ponto B e, mantendo o mouse pressionado, movimente-o.
4) Você encontrará registrados no applet :
- a medida dos lados do quadrado maior
- a medida dos lados do quadrado menor.
5) Lembre-se de que o GeoGebra fornece valores aproximados para as medidas apresentadas.
OBMEP_srg, criado com o GeoGebra
Observamos que o applet ajuda na visualização do resultado;
mas, matematicamente, não substitui sua demonstração.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |