M_Sala de ajuda: Funções – Imagem direta e imagem inversa

Funções

Imagem direta e imagem inversa

Fixada uma função, as vezes é necessário estudarmos o comportamento dessa função apenas em parte do domínio ou do contradomínio. Dessa forma, dados uma função $f:A \rightarrow B$ e conjuntos $X$ e $Y$ tais que $X\subset A$ e $Y \subset B$ é bastante conveniente se definir matematicamente "para onde a $f$ leva os elementos de $X$ " e "de onde vieram os elementos que a $f$ levou para $Y$ ".

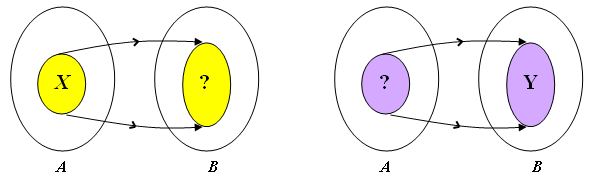
fig044

✐ Dada a função

$f:A \rightarrow B$ e sendo

$X$ um subconjunto de

$A$ , chamamos imagem direta de $X$ por $f$ , e denotamos

$f(X)$ , o seguinte subconjunto de

$B$ :

$\qquad \qquad f(X)=\{f(x)$ tal que $x\in X\}$ .
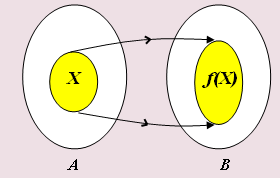
fig047

✐ Dada uma função

$f:A \rightarrow B$ e sendo

$Y$ um subconjunto de

$B$ , chamamos imagem inversa de $Y$ por $f$ , e denotamos

$f^{-1}(Y)$ , o seguinte subconjunto de

$A$ :

$\qquad \qquad f^{-1}(Y)=\{x\in X$ tal que $f(x)\in Y\}$ .
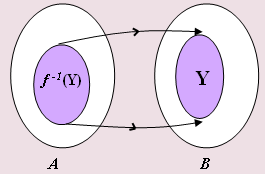
fig048

Para que você vá além das duas definições aqui apresentadas, acrescentamos mais algumas páginas do livro do professor Elon Lages Lima ao material disponibilizado sobre funções.
Para ler o material, clique no botão abaixo.

Ler o material

Para copiar o material, clique no próximo botão.

Baixar o arquivo

Bons estudos!