Problema
(Indicado a partir do 1º ano do E. M.)
É possível construir dois triângulos não congruentes, mas que possuam cinco pares de elementos (lados ou ângulos internos) ordenadamente congruentes?
Solução
Entre ângulos e lados um triângulo tem seis elementos – três lados e três ângulos. Assim, temos apenas duas possibilidades para os dois triângulos do problema: ou eles têm dois pares de ângulos internos e três pares de lados ordenadamente congruentes ou eles têm três pares de ângulos internos e dois pares de lados ordenadamente congruentes.
Observe que se os dois triângulos possuíssem dois pares de ângulos internos e três pares de lados ordenadamente congruentes, então o caso LLL nos permitiria afirmar que os triângulos são congruentes, contrariando a hipótese do problema.
Logo, a primeira situação não ocorre e, portanto, os dois triângulos em questão possuem três pares de ângulos internos e dois pares de lados ordenadamente congruentes.
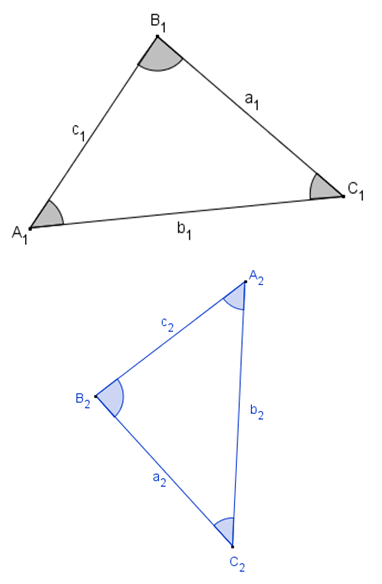 |
Por terem dois ângulos congruentes, os triângulos são semelhantes: indicaremos a razão de semelhança por [tex]k[/tex].
tais que
Indicaremos as medidas dos lados pela mesma letra do vértice oposto; assim, como os triângulos são semelhantes, temos ainda:
sendo a razão de semelhança [tex]k[/tex] um número real positivo. |
Analisemos um pouco mais as medidas [tex]a_1, \, b_1, \, c_1, \, a_2, \, b_2, \, c_2[/tex].
Observe que se tivéssemos [tex]a_1 = a_2[/tex] ou [tex]b_1 = b_2[/tex] ou [tex]c_1 = c_2[/tex], os dois triângulos seriam congruentes pelo caso ALA, o que contraria a hipótese do problema. Assim [tex]a_1 \neq a_2[/tex] e [tex]b_1 \neq b_2[/tex] e [tex]c_1 \neq c_2[/tex]; e como [tex]a_1 = k a_2[/tex], [tex]b_1 = k b_2[/tex], [tex]c_1 = k c_2[/tex], então [tex]k \ne 1[/tex].
Mas, sabemos que há dois pares de lados ordenadamente congruentes; então considere, sem perda de generalidade, que [tex]a_1 = b_2[/tex] e [tex]b_1 = c_2[/tex] (isso significa que se qualquer uma das outras possibilidades ocorrer, o raciocínio que faremos a seguir poderá também ser feito).
Assim, [tex]b_2 = k a_2[/tex] e [tex]c_2 = k b_2[/tex]. Substituindo o valor de [tex]b_2[/tex] da primeira na segunda igualdade, temos [tex]c_2 = k^2 a_2[/tex].
Deste modo, os lados dos triângulos [tex]A_1B_1C_1[/tex] e [tex]A_2B_2C_2[/tex] medem [tex](k a_2\, ,\, k^2 a_2\, ,\, k^3 a_2)[/tex] e [tex](a_2\, ,\, k a_2\, ,\, k^2 a_2)[/tex], respectivamente.
Devemos, agora, verificar sob quais condições esses números representam, de fato, medidas de lados de um triângulo.
Como [tex]k \neq 1[/tex], há duas possibilidades a analisar: [tex]0\lt k \lt 1[/tex] e [tex]k \gt 1[/tex].
[tex](i)[/tex] Para [tex]k \gt 1[/tex], as condições de existência dos triângulos se resumem a [tex] \, \, k^3a_2 \,\lt\,ka_2 \, +\, k^2a_2 \, \, [/tex] e [tex] \, \, k^2a_2 \,\lt\,a_2\, +\, ka_2[/tex]; mas, como [tex]a_2 [/tex] é um comprimento, então [tex]a_2 \gt 0[/tex]. Assim, [tex]k^3 \,\lt\,k \, +\, k^2[/tex] e [tex]k^2 \,\lt\,1\, +\, k[/tex].
Note que essas duas desigualdades são equivalentes, pois a primeira pode ser obtida a partir da segunda pela multiplicação de ambos os membros por [tex]k[/tex].
Resolvendo a inequação [tex]k^2 \,-\,k\,-\,1\,\lt\,0[/tex], obtemos [tex]\dfrac{1-\sqrt{5}}{2}\,\lt\,k\,\lt\,\dfrac{1+\sqrt{5}}{2}[/tex].
Mas, sendo [tex]k \gt 1 \, [/tex] e [tex] \, \dfrac{1-\sqrt{5}}{2} \lt 1[/tex], concluímos que:
[tex]\qquad \qquad 1\,\lt\,k\,\lt\,\dfrac{1+\sqrt{5}}{2}[/tex]. [tex]\qquad \qquad(I)[/tex]
[tex](ii)[/tex] Para [tex]0 \lt k \lt 1[/tex], as condições de existência dos triângulos se resumem a [tex]ka_2 \,\lt\,k^3a_2 \, +\, k^2a_2 \, [/tex] e [tex] \, a_2 \,\lt\,k^2a_2\, +\, ka_2[/tex]. Como [tex]a_2 \gt 0[/tex], ficamos com as desigualdades [tex]k \,\lt\,k^3 \, +\, k^2 \, [/tex] e [tex] \, 1 \,\lt\,k^2\, +\, k[/tex].
Essas duas desigualdades também são equivalentes, pois a primeira pode ser obtida a partir da segunda pela multiplicação de ambos os membros por [tex]k[/tex].
Resolvendo a inequação [tex]k^2 \,+\,k\,-\,1\,\gt\,0[/tex], obtemos [tex]k\,\lt\,\dfrac{-1-\sqrt{5}}{2} \, [/tex] ou [tex] \, k\,\gt\,\dfrac{-1+\sqrt{5}}{2}[/tex].
Como [tex]0\,\lt\,k\,\lt\,1 \, \, [/tex] e [tex]\dfrac{-1-\sqrt{5}}{2} \lt 0 \, [/tex], temos:
[tex]\qquad \qquad \dfrac{-1+\sqrt{5}}{2}\,\lt\,k\,\lt\,1[/tex]. [tex]\qquad \qquad (II)[/tex]
Finalmente, temos que:
- a condição [tex](I)[/tex] nos garante que é possível obter dois triângulos satisfazendo as hipóteses do problema, para todo [tex]k[/tex] real tal que [tex]1\,\lt\,k\,\lt\,\dfrac{1+\sqrt{5}}{2}[/tex];
- a condição [tex](II)[/tex] garante que é possível também é possível obter dois triângulos satisfazendo as hipóteses do problema, para todo [tex]k[/tex] real tal que [tex]\dfrac{-1+\sqrt{5}}{2}\,\lt\,k\,\lt\,1[/tex];
dessa forma, por [tex](I)[/tex] e [tex](II)[/tex], segue que para [tex] \dfrac{-1+\sqrt{5}}{2}\,\lt\,k\,\lt\,\dfrac{1+\sqrt{5}}{2}[/tex], com [tex] \, k \neq 1[/tex], é possível construir dois triângulos não congruentes, mas que possuam cinco pares de elementos ordenadamente congruentes.
Particularmente, tomando [tex]k = \sqrt{2}[/tex] temos dois triângulos semelhantes com lados medindo [tex](\sqrt{2}\, ,\, 2\, ,\,2\sqrt{2})[/tex] e [tex](2\, ,\, 2\sqrt{2}\, ,\,4)[/tex] que satisfazem as condições do problema.
 |
O número [tex]\frac{1+\sqrt{5}}{2}[/tex] é bastante famoso. Ele é conhecido como razão áurea e comumente é representado pela letra grega [tex]\phi[/tex]. |
Solução elaborada pelos Moderadores do Blog.
