Problemas
Se você gosta de resolver problemas, aqui vão alguns…
Problema 1:
A figura abaixo não é um polígono. Por quê?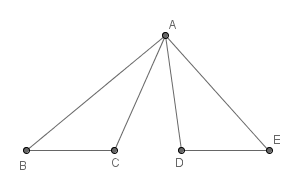
Problema 2:
Quantas diagonais tem um polígono convexo de 4 lados?
E um com 5 lados?
E um com 6 lados?
E um com 7 lados?
E um com 13 lados?
E um com 101 lados?
Problema 3:
Quantas diagonais tem um polígono convexo de n lados?
Justifique.
Problema 4:
Verifique a veracidade da seguinte afirmação:
Se uma diagonal de um polígono é externa a ele, então o polígono não é convexo.
Problema 5:
Qual é a soma, em graus, das medidas dos ângulos internos de um polígono convexo de n lados?
Problema 6:
Qual é o polígono convexo que possui 65 diagonais?
Resposta: É o polígono de 13 lados.
Problema 7:
Qual o polígono convexo cujo número de diagonais é igual ao quádruplo do número de lados?
Resposta: Undecágono.
Problema 8:
As mediatrizes de dois lados consecutivos de um polígono convexo regular formam entre si um ângulo de 24°. Determine o número de diagonais desse polígono.
Resposta: 90 diagonais.
Problema 9:
Prolongando-se os lados AB e CD de um polígono convexo regular, obtém-se um ângulo de 132°.
Que polígono é esse?
Resposta: É o polígono convexo regular de 15 lados (pentadecágono).
Problema 10:
Um dos ângulos internos de um polígono regular convexo mede 18°.
Calcule o número de lados desse polígono.
Problema 11:
Em um polígono regular convexo ABCDE , o ângulo BÂD mede 18°.
Qual o número de lados desse polígono?
Resposta: 20 lados (icoságono).
Um problema e um applet
Um polígono que tenha todos os seus lados com o mesmo comprimento é denominado de polígono equilátero. Um polígono que tenha todos os seus ângulos internos com a mesma medida é denominado de polígono equiângulo.
Assim, uma pergunta natural seria: Um polígono equilátero é necessariamente equiângulo?
De forma explícita, se um polígono tem todos seus lados com um mesmo comprimento, então todos os seus ângulos internos também terão a mesma medida?
O applet abaixo ajudará você com a resposta.

