Voltar para .Sala de Estudo: Um pouco sobre divisibilidade (Parte 2)

Um pouco sobre divisibilidade: TFA – problemas

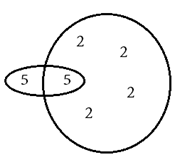
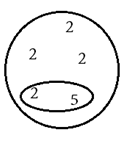
Teorema Fundamental da Aritmética

Problemas

Problema 1: O número [tex]2^4 \cdot 5[/tex] é divisível por [tex]2[/tex]?

Sim, já que [tex]2[/tex] é um dos fatores na decomposição do número dado.

Problema 2: O número [tex]2^4\cdot 5[/tex] é divisível por [tex]3[/tex]?

Não, já que a decomposição deste número não contém o número primo [tex]3[/tex].

Problema 3: O número [tex]2^4\cdot 5 [/tex] é divisível por [tex]8[/tex]?

Sim, já que [tex]8=2^3[/tex] e existem quatro fatores iguais a [tex]2[/tex] na decomposição do número dado.

Problema 4: O número [tex]2^4\cdot 5 [/tex] é divisível por [tex]25[/tex]?

Não, já que [tex]25=5^2[/tex] e só existe um [tex]5[/tex] na decomposição do número dado.

tfa1

Problema 5: O número número [tex]2^4\cdot 5 [/tex] é divisível por [tex]10[/tex]?

Sim, já que [tex]10=2\cdot5[/tex] e a decomposição do número dado contém ambos os números primos [tex]2[/tex] e [tex]5[/tex].

tfa2

Problema 6: O número [tex]A[/tex] não é divisível por [tex]5[/tex]. É possível que o número [tex]2A[/tex] seja divisível por [tex]5[/tex]?

Não, pois para que [tex]2A[/tex] seja divisível por [tex]5[/tex] é necessário e suficiente que na decomposição do número [tex]2A[/tex]apareça o fator [tex]5[/tex]. Como esse fator não se encontra na fatoração do número [tex]2[/tex] nem na fatoração do número [tex]A[/tex] (afirmado pelo enunciado), podemos afirmar que [tex]2A[/tex] não é divisível por [tex]5[/tex]

Problema 7: O número [tex]A[/tex] é par. É verdade que o número [tex]2A[/tex] tem que ser divisível por [tex]4[/tex]?

Inicialmente, lembramos que [tex]4=2^2[/tex]. A resposta ao problema é sim, pois observe que, se [tex]A[/tex] é par, então [tex]A = 2n[/tex], para algum número natural [tex]n[/tex].
Portanto, [tex]2A = 2\cdot 2n[/tex], ou seja, concluímos que há pelo menos dois fatores [tex]2[/tex] na decomposição do número [tex]2A[/tex].

Problema 8: O número [tex]3A[/tex] é divisível por [tex]7[/tex]. É verdade que o número [tex]A[/tex] tem que ser divisível por [tex]7[/tex]?

Sim, pois a decomposição de [tex]3A[/tex] contém [tex]7[/tex], mas a decomposição de [tex]3[/tex] não.

Problema 9: O número [tex]21A[/tex] é divisível por [tex]6[/tex]. É verdade que [tex]A[/tex] tem que ser divisível por [tex]6[/tex]?

Não. Por exemplo, [tex]A[/tex] poderia ser igual a [tex]2[/tex]. Como [tex]6 = 2\cdot 3[/tex], então para que um número seja divisível por [tex]6[/tex] é necessário que este tenha, em sua fatoração, os fatores [tex]2[/tex] e [tex]3[/tex]. Como [tex]21 = 3\cdot 7[/tex], então podemos ter a certeza de que o número [tex]A[/tex] possui um fator [tex]2[/tex] em sua decomposição, mas não é necessária a presença do fator [tex]3[/tex]. Portanto, não é preciso que A seja divisível por [tex]6[/tex].

Problema 10: Encontre o menor número natural [tex]n[/tex] tal que [tex]n![/tex] é divisível por [tex]990[/tex].

Como [tex]990=2\cdot3^2\cdot5\cdot11[/tex], para que [tex]n![/tex] seja divisível por [tex]990[/tex], é necessário que em sua decomposição haja todos esses fatores.
Mas [tex]11[/tex] é primo, logo ele mesmo tem que estar contido no produto.
Observe que [tex]11![/tex] é divisível por [tex]2[/tex], por [tex]3^2[/tex] e por [tex]5[/tex].
Assim, [tex]n=11[/tex] é o menor valor possível, pois o fatorial de qualquer outro número menor que este não terá o fator [tex]11[/tex] em sua decomposição.

Os próximos problemas são para vocês fazerem!

Problema 11: O número [tex]5A[/tex] é divisível por [tex]3[/tex]. É verdade que [tex]A[/tex] tem que ser divisível por [tex]3[/tex]?

Problema 12: Encontre todos os números naturais [tex]x[/tex] e [tex]y[/tex] tais que [tex]x^2-y^2=31[/tex]. (Resposta: Apenas [tex]x=16[/tex] e [tex]y=15[/tex])

Problema 13: (OBM 2010 – F1N2) Qual das alternativas apresenta um divisor de [tex]3^5 \times 4^4 \times 5^3[/tex] ?
a) [tex]42\qquad [/tex] b) [tex]45\qquad [/tex] c) [tex]52\qquad [/tex] d) [tex]85\qquad [/tex] e) [tex]105\qquad [/tex](Resposta: b)

Equipe COM – OBMEP

Voltar para Sala Principal do TFA

Link permanente para este artigo: http://clubes.obmep.org.br/blog/teoria-dos-numeros-um-pouco-sobre-divisibilidade-parte-2/um-pouco-sobre-divisibilidade-tfa-problemas/