Problema
(Indicado a partir do 2º ano do E. M.)
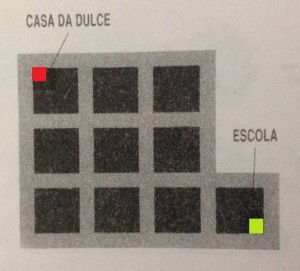
Dulce estuda na escola que fica na outra ponta do bairro em que mora, como é possível observar no mapa abaixo. Ela vai caminhando para aula e percebeu que havia muitas maneiras diferentes de chegar à escola (devido à geometria do bairro), seguindo sempre por um dos caminhos mais curtos.
Quantos caminhos mais curtos há da casa de Dulce até a escola?

Ajuda
✏ Princípio Fundamental da Contagem, ou Princípio Multiplicativo, para dois eventos: Se
- um evento E1 puder ocorrer de [tex] m_1 [/tex] maneiras,
- um evento E2 puder ocorrer de [tex]m_2 [/tex] maneiras,
e esses eventos forem independentes entre si (isto é, a ocorrência de um não muda a quantidade de possibilidades para a ocorrência do outro), então a quantidade de maneiras em que os dois eventos ocorrem ao mesmo tempo é
[tex]\qquad \qquad \boxed{m_1\times m_2 }\, .[/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
✏ Princípio Aditivo de Contagem, para dois eventos: Se
- um evento E1 puder ocorrer de [tex] m_1 [/tex] maneiras,
- um evento E2 puder ocorrer de [tex]m_2 [/tex] maneiras,
e esses eventos forem independentes entre si (isto é, a ocorrência de um não muda a quantidade de possibilidades para a ocorrência do outro), então a quantidade de maneiras em que ocorre um dos dois eventos (E1 ou E2) é
[tex]\qquad \qquad \boxed{m_1+ m_2 }\, .[/tex]
Solução
Na figura abaixo, observe que para Dulce ir de casa à escola por um caminho mais curto possível, invariavelmente ela deverá passar por apenas um dos cruzamentos indicados: [tex]A[/tex] ou [tex]B[/tex].
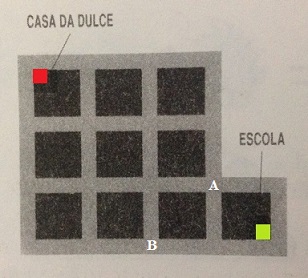
Observe, ainda, que “o número de possibilidades de Dulce ir de sua casa até o ponto [tex]A[/tex]” é igual “ao número de possibilidades de ela ir de sua casa até o ponto [tex]B[/tex]”, já que, nas duas situações, ambos os pontos estão em um vértice oposto ao da casa de Dulce, em retângulos com o mesmo tamanho.
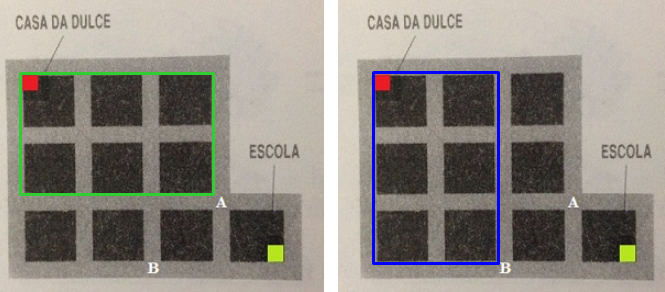
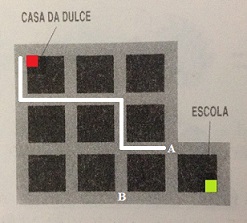
Avaliemos, então, quantas são as possibilidades de Dulce ir de sua casa até o ponto [tex]A[/tex] (já que este é o mesmo número de possibilidades de ela ir de sua casa até o ponto [tex]B[/tex]). Neste caso, ela deverá andar duas quadras para baixo (representemos por B B) e três quadras para direita (representemos por D D D). Note que qualquer caminho feito por Dulce corresponde, então, a uma sequência das letras B e D, com as respectivas repetições (2 e 3). Por exemplo, para a situação representada abaixo, corresponderia a sequência B D D B D.
Assim, temos que avaliar quantas são as maneiras de distribuirmos essas cinco letras em cinco lugares possíveis na sequência. Comecemos o preenchimento com a letra B; as letras D ocuparão os espaços restantes.
Se temos 5 lugares disponíveis, para a primeira letra B temos 5 possibilidades. Feito o primeiro preenchimento, teremos 4 possibilidades para a segunda letra B. Aparentemente, teríamos 5 × 4 = 20 possibilidades ao total, pelo princípio multiplicativo de contagem. Entretanto, como se tratam de letras iguais, independente de qual seja a primeira ou a segunda colocada, teremos casos duplicados (convença-se disso!), o que nos obriga a dividir o total por 2, ou seja, existem, de fato, 10 casos distintos possíveis de colocações para as letras B.
- Como de [tex]A[/tex] até a escola existem 2 possibilidades por caminhos mais curtos (B D e D B), Dulce terá então 10 × 2 = 20 possibilidades de chegar à escola passando por [tex]A[/tex].
- Já de [tex]B[/tex] até a escola, existe apenas uma possibilidade de caminho mais curto (D D). Então, Dulce terá 10 × 1 = 10 possibilidades de chegar à escola passando por [tex]B[/tex].
Como Dulce pode ir para a escola passando por [tex]A[/tex] ou [tex]B[/tex], devemos somar o total de possibilidades em cada caso (princípio aditivo de contagem), o que resulta em 30 maneiras possíveis de Dulce ir até à escola por caminhos mais curtos.
Solução elaborada pelos Moderadores do Blog.
