Problema
(Indicado a partir do 6º ano do E. F.)
É possível cobrir uma malha quadriculada 6X6 com 18 dominós que ocupem, cada um, exatamente 2 quadrados adjacentes, sem que exista qualquer linha falha?
Consideramos uma linha falha qualquer segmento que vá de um lado a outro do tabuleiro sem que atravesse qualquer dominó.
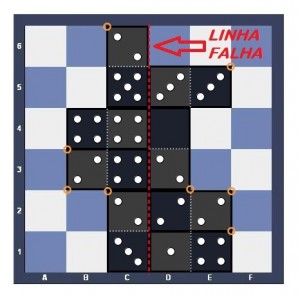
Se você quiser ler um pouco mais sobre linha falha, clique aqui.
Na Ludoteca do BLOG dos Clubes de Matemática da OBMEP (mais precisamente em Aparatos >>>>Um desafio legal!) é possível fazer uma simulação para este desafio.
Em http://www.geogebratube.org/material/show/id/119837 também é possível acessar o aparato e fazer algumas tentativas para ajudar a chegar à conclusão . . .
Solução
Em um tabuleiro 6×6 existem 5 linhas na horizontal e 5 linhas na vertical, as quais podem ser interceptadas por um dominó. Mas é importante notar que um dominó colocado de forma a cobrir dois quadrados do tabuleiro ou bem interceptará uma linha vertical, ou bem interceptará uma linha horizontal; mas nunca ambas simultaneamente.

Nosso tento é cobrir um tabuleiro 6×6, sem que haja qualquer linha falha. Em outras palavras, isto quer dizer que todos os segmentos (verticais e horizontais) no interior do tabuleiro devem ser interceptados por, pelo menos, um dominó.
Mas, antes de mais nada, observamos que:
- Se uma determinada linha for interceptada por um dominó, invariavelmente será interceptada por outro também.
Acompanhem, a seguir, por que isso acontece.
- Se um dominó intercepta uma determinada linha, esta dividirá o tabuleiro em duas regiões (como ilustram as áreas verde e rosa da representação acima). Como cada uma dessas regiões tinha inicialmente um número par de casas e o dominó cobriu uma casa de cada uma delas, ficamos com um número ímpar de casas descobertas em cada região. Mas cada dominó cobre duas casas; logo, não conseguiremos distribuir os dominós restantes de modo que cada um deles cubra duas casas de uma só região. Portanto, necessariamente haverá outro dominó (pelo menos) interceptando a mesma linha.
A partir dessa observação já conseguimos resolver o problema!
Observe que temos um total 10 linhas (5 horizontais e 5 verticais) a serem interceptadas por dominós e para cruzar por cada uma delas precisamos de, pelo menos, 2 dominós. Isso significa que precisaríamos de, no mínimo, 20 dominós para cobrir o tabuleiro nessas condições; no entanto, isso não é possível, tendo em vista que dispomos de apenas 18 dominós.
Assim, é impossível cobrir o tabuleiro 6×6 com 18 dominós, sem que haja qualquer linha falha.
Solução elaborada pelos Moderadores do Blog.
