Problema
(Indicado a partir do 9º ano do E. F.)
(UNIFOR, 2012) A figura abaixo representa o perfil de uma escada cujos degraus têm todos a mesma extensão (veja a figura), além de mesma altura. Se [tex]AB=3\text{ m}[/tex] e [tex]B\hat{C}A=30^\circ[/tex], qual é a medida da extensão de cada degrau?
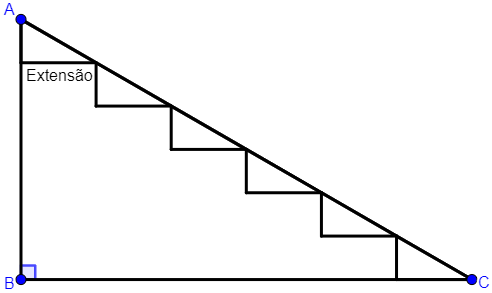

Lembretes e notações
(I) A tangente do ângulo de [tex]30^\circ[/tex] é dada por [tex]\tan 30^\circ=\frac{1}{\sqrt3}[/tex].
(II) Caso de congruência A.L.A. (ângulo – lado – ângulo): Se dois triângulos têm ordenadamente congruentes dois ângulos e o lado compreendido por eles, então estes triângulos são congruentes. (Se você não se lembra dos casos de congruência de triângulos, clique AQUI.)
Solução
Inicialmente, observe que o segmento do início da escada, ilustrado em rosa na próxima figura, tem a extensão de um degrau:
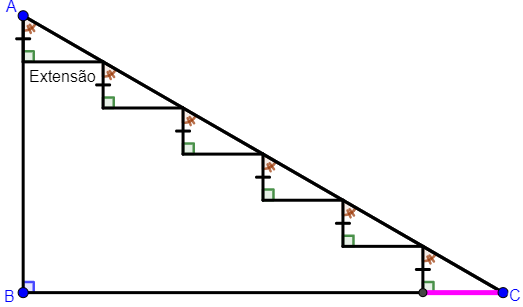
De fato, os triângulos formados entre o perfil da escada e o segmento [tex]\overline{AC}[/tex] são todos congruentes pelo caso A-L-A.
Assim, a medida do cateto [tex]{BC}[/tex] do triângulo retângulo [tex]ABC[/tex] equivale à soma da extensão de seis degraus.
Observe que [tex]\dfrac{AB}{BC}=\tan 30^\circ=\dfrac{1}{\sqrt{3}}[/tex]. Logo, [tex]BC=AB\cdot \sqrt{3}=3\sqrt{3}[/tex]. Portanto, a extensão de cada degrau é de [tex]\dfrac{3\sqrt{3}}{6}=\dfrac{\sqrt{3}}{2}\approx 0,87 \text{ m}.[/tex]
Solução elaborada pelos Moderadores do Blog.
