Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F.- Nível de dificuldade: Difícil)
Dado um quadrado [tex]ABCD[/tex], escolhemos um ponto [tex]P[/tex], no lado [tex]\overline{CD}[/tex], e um ponto [tex]Q[/tex], no lado [tex]\overline{DA}[/tex], de modo que o ângulo determinado pelos segmentos [tex]\overline{BP}[/tex] e [tex]\overline{BQ}[/tex] meça [tex]45^\circ[/tex], conforme ilustra a figura a seguir.
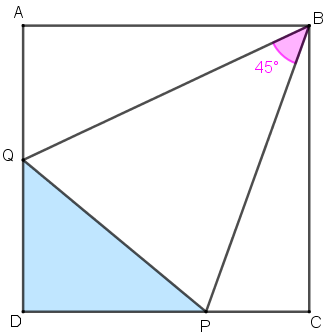
Se o comprimento de cada lado do quadrado [tex]ABCD[/tex] é [tex]x[/tex], qual é o perímetro do triângulo [tex]PDQ[/tex] em função de [tex]x[/tex]?
Lembrete e Notações
✏ Caso de congruência de triângulos L.A.L. (lado – ângulo – lado): Se dois triângulos têm ordenadamente congruentes dois lados e o ângulo por eles definido, então estes triângulos são congruentes. (Se você não se lembra desse resultado, clique AQUI.).
✏ Denotaremos o segmento de reta definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e seu respectivo comprimento por [tex]XY[/tex].
Solução
Denotaremos as medidas em graus dos ângulos [tex]A\hat{B}Q[/tex] e [tex]P\hat{B}C[/tex] por [tex]a\,[/tex] e [tex]\,b[/tex], respectivamente.
Inicialmente, observamos que [tex]a+45^\circ +b=90^\circ[/tex]; assim, [tex]\boxed{a+b=45^\circ}\,.[/tex]
Agora, no prolongamento do segmento [tex]\overline{AD}[/tex] vamos tomar o ponto [tex]P'[/tex] tal que [tex]AP’=CP[/tex] e construir o triângulo [tex]BAP'[/tex], conforme indica a figura a seguir.
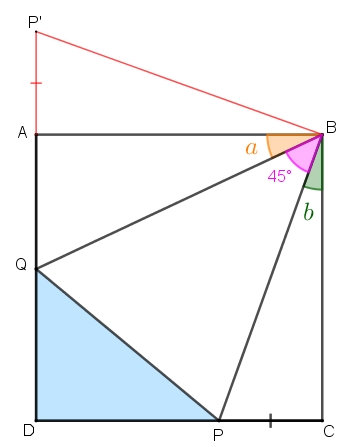
Como [tex]ABCD[/tex] é um quadrado, pelo Caso de congruência de triângulos L.A.L., os triângulos [tex]BCP[/tex] e [tex]BAP'[/tex] são congruentes; portanto, [tex]BP’=BP\,[/tex] e a medida do ângulo [tex]A\hat{B}P'[/tex] é [tex]b\,.[/tex]
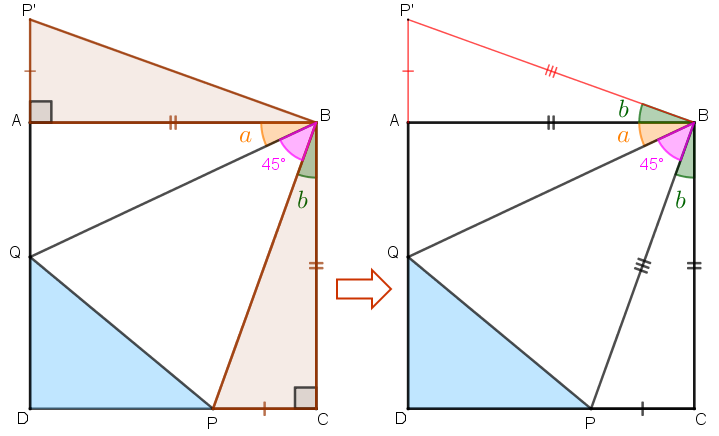
Como sabemos que [tex]a+b=45^\circ[/tex], o Caso de congruência de triângulos L.A.L. também garante a congruência dos triângulos [tex]QBP[/tex] e [tex]QBP’\,[/tex].
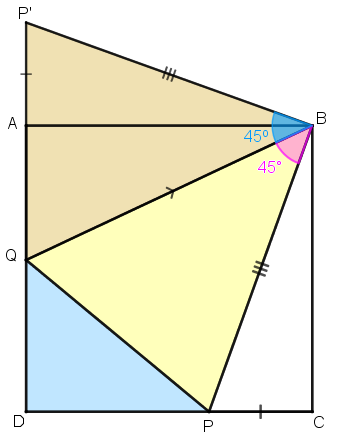
Com isso, concluímos que [tex]\boxed{PQ=P’Q}[/tex] e já podemos, finalmente, calcular o perímetro [tex]\textcolor{#5CB3FF}{Perim}[/tex] do triângulo [tex]PDQ:[/tex]
[tex]\quad \\
\quad \begin{align*}\textcolor{#5CB3FF}{Perim}&=QD+DP+PQ\\
&=QD+DP+P’Q\\
&=QD+DP+\left(P’A+AQ\right)\\
&=\left(AQ+QD\right)+DP+P’A\\
&=AD+DP+P’A\\
&=AD+DP+PC\\
&=AD+DC\\
&=x+x=2x\,.\\
\end{align*}
[/tex]
Portanto, o perímetro do triângulo [tex]PDQ[/tex] é [tex]\fcolorbox{black}{#eee0e5}{$2x$}\,.[/tex]
Um applet para ajudar
Instruções:
(1) Movimente os pontos [tex]\color{red}{P}[/tex] e [tex]\color{#7D7DFF}{Q}[/tex] que aparecem no applet até obter um ângulo [tex]Q\hat{B}P[/tex] de [tex]45^\circ[/tex], como previsto no problema. Definido esse ângulo, compare a sua resposta com a resposta do applet, observando que no applet construímos um quadrado com lados medindo [tex]x=5\,.[/tex]
(2) Para movimentar o ponto [tex]\color{red}{P}[/tex] (ou o ponto [tex]\color{#7D7DFF}{Q}[/tex]), basta clicar sobre ele com o botão esquerdo do mouse, manter o botão pressionado e fazer o movimento lentamente. (Se você estiver utilizando um celular ou um tablet, basta tocar levemente no ponto [tex]\color{red}{P}[/tex] (ponto [tex]\color{#7D7DFF}{Q}[/tex]) e movimentá-lo horizontalmente (verticalmente).)
(3) Lembre-se de que o GeoGebra fornece valores aproximados e que a visualização de várias situações particulares de um fato matemático não substitui sua demonstração.
OBMEP_ srdg, criado com o GeoGebra
Dica: Você poderá fazer um movimento “mais fino” dos pontos [tex]\color{red}{P}[/tex] e [tex]\color{#7D7DFF}{Q}[/tex] utilizando seu teclado. Para isso:
- Clique sobre [tex]\color{red}{P}[/tex] com o botão esquerdo do mouse. Em seguida, mantenha a tecla Shift do teclado apertada e faça os movimentos utilizando as teclas “mover para direita” e “mover para esquerda”.
- Clique sobre [tex]\color{#7D7DFF }{Q}[/tex] com o botão esquerdo do mouse. Em seguida, mantenha a tecla Shift do teclado apertada e faça os movimentos utilizando as teclas “mover para cima” e “mover para baixo”.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
