Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F.- Nível de dificuldade: Difícil)
Na figura abaixo, ABCD é um quadrado e ABEFG é um pentágono regular.
Qual a medida do ângulo determinado pelos segmentos GB e GD ?
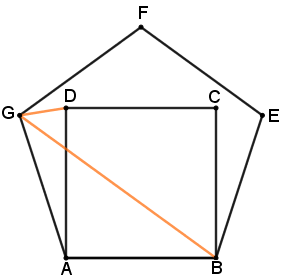
Adaptado da XIV ONM, 2014.

Lembretes e notações
(1) A soma das medidas dos ângulos internos de qualquer triângulo é [tex]180^\circ.[/tex]
(2) Cada ângulo interno de um pentágono regular mede [tex]108^\circ.[/tex]
(3) Cada ângulo interno de um quadrado mede [tex]90^\circ.[/tex]
(4) Todo triângulo isósceles possui os ângulos da base com a mesma medida.
✐ Denotaremos o ângulo de vértice [tex]V[/tex] e definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]X\hat{V}Y[/tex] e a sua medida por [tex]m(X\hat{V}Y)\,.[/tex]
✐ Denotaremos o segmento de reta definido por dois pontos, digamos [tex]X[/tex] e [tex]Y[/tex], por [tex]\overline{XY}[/tex] e seu respectivo comprimento por [tex]XY[/tex].
Solução
- Vamos analisar o triângulo [tex]AGD[/tex].
- Agora, vamos analisar o triângulo [tex]ABG[/tex] para obter a medida do ângulo [tex]A\hat{G}B\,.[/tex]
Observe que o segmento [tex]\overline{AB}[/tex] é lado do quadrado e do pentágono; logo, os dois polígonos têm lados com o mesmo comprimento. Dessa forma, os segmentos [tex]\overline{AG}\,[/tex] e [tex]\,\overline{AD}[/tex] têm o mesmo comprimento e, portanto, o triângulo [tex]AGD[/tex] é isósceles.
Vamos determinar, inicialmente, a medida do ângulo [tex]G\hat{A}D[/tex], utilizando os Lembretes (2) e (3):
[tex]\qquad m(G\hat{A}D)=m(G\hat{A}B)-m(D\hat{A}B)\\
\qquad m(G\hat{A}D)=108^\circ-90^\circ\\
\qquad \boxed{m(G\hat{A}D)=18^\circ},[/tex]
já que [tex]G\hat{A}B[/tex] e [tex]D\hat{A}B[/tex] são ângulos internos do pentágono e do quadrado, respectivamente.
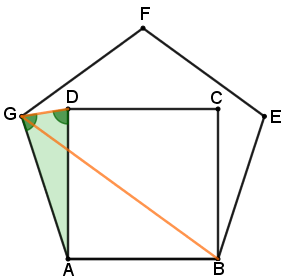
Com isso, utilizando os Lembretes (1) e (4), segue que:
[tex]\qquad m(D\hat{G}A)+m(G\hat{D}A)+m(G\hat{A}D)=180^\circ\\
\qquad 2\,m(D\hat{G}A)+m(G\hat{A}D)=180^\circ\\
\qquad 2\,m(D\hat{G}A)+18^\circ=180^\circ\\
\qquad 2\,m(D\hat{G}A)=162^\circ\\
\qquad \boxed{\textcolor{#009900}{m(D\hat{G}A)=81^\circ}}\,.[/tex]
Como os dois polígonos têm lados com o mesmo comprimento, [tex]AG=AB[/tex] e, portanto, [tex]ABG[/tex] é um triângulo isósceles.
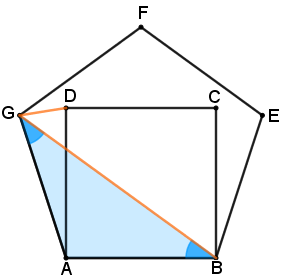
Então, utilizando os Lembretes (1), (2) e (4), segue que:
[tex]\qquad m(A\hat{G}B)+m(A\hat{B}G)+m(B\hat{A}G)=180^\circ\\
\qquad 2\,m(A\hat{G}B)+m(B\hat{A}G)=180^\circ\\
\qquad 2\,m(A\hat{G}B)+108^\circ=180^\circ\\
\qquad 2\,m(A\hat{G}B)=72^\circ\\
\qquad \boxed{ \textcolor{#0099FF}{m(A\hat{G}B)=36^\circ}}\,.[/tex]
Pronto, já temos condições de determinar a medida do ângulo [tex]B\hat{G}D[/tex]:
[tex]\qquad \textcolor{#FF7F00}{m(D\hat{G}B)}=\textcolor{#009900}{m(D\hat{G}A)}-\textcolor{#0099FF}{m(A\hat{G}B)}\\
\qquad \textcolor{#FF7F00}{m(D\hat{G}B)}=\textcolor{#009900}{81^\circ}-\textcolor{#0099FF}{36^\circ}\\
\qquad \textcolor{#FF7F00}{m(D\hat{G}B)}=\textcolor{#FF7F00}{45^\circ}\\
[/tex]
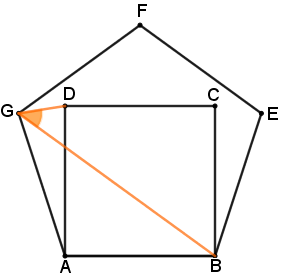
Portanto, a medida do ângulo determinado pelos segmentos GB e GD é [tex]\fcolorbox{black}{#eee0e5}{$45^\circ$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
