Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 1º ano do E. M.- Nível de dificuldade: Muito Difícil)
Verifique que, para qualquer número natural [tex]n[/tex], o número natural da forma [tex]\; \underbrace{44\cdots 4}_{n}\underbrace{22 \cdots 2}_{n+1}5[/tex] é um quadrado perfeito.
Extraído da XIV Olimpíada Regional de Matemática Santa Catarina, 2011.

Lembrete
Dada uma progressão geométrica finita, [tex](a_1,a_1q, a_1q^2,\cdots,a_1q^{m-1})[/tex], de razão [tex]q\ne1[/tex], a soma [tex]S[/tex] desses [tex]m[/tex] termos é dada por
\begin{equation}
S=(a_1+a_1q+a_1q^2+\cdots+a_1q^{m-1})=\dfrac{a_1\cdot (q^m-1)}{q-1}.
\end{equation}
Solução
Fixado um número natural [tex]n[/tex], seja [tex]\;N= \underbrace{44\cdots 4}_{n}\underbrace{22 \cdots 2}_{n+1}5[/tex].
Inicialmente, observe que se [tex]n=0[/tex], então [tex]N[/tex] não tem algarismos [tex]4[/tex] e tem um algarismo [tex]2[/tex], além do algarismo [tex]5[/tex]. Assim, [tex]N=25=5^2[/tex] e, portanto, [tex]N[/tex] é um quadrado perfeito.
Para [tex]n \gt 0[/tex] , vamos escrever o número [tex]\;N= \underbrace{44\cdots 4}_{n}\underbrace{22 \cdots 2}_{n+1}5[/tex] de outra forma, para facilitar a visualização da quantidade de zeros que utilizaremos para representar [tex]N[/tex] na forma decimal.
Observe que [tex]N[/tex] é o resultado da seguinte adição:
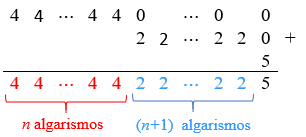
Assim,
[tex]\qquad N=4\cdot 10^{2n+1}+4\cdot 10^{2n}+\cdots+4\cdot 10^{n+3}+4\cdot 10^{n+2}+\\
\qquad\qquad 2\cdot 10^{n+1}+2\cdot 10^{n}+\cdots +2\cdot 10^{2}+2\cdot 10^{1}+\\
\qquad\qquad 5[/tex]
e, portanto, segue que:
[tex]\qquad N=4\cdot 10^{2n+1}+\cdots+4\cdot 10^{n+2}+2\cdot 10^{n+1}+\cdots+2\cdot 10^{1}+5[/tex]
[tex]\qquad N=4\cdot\left(10^{2n+1}+\cdots +10^{n+2}\right)+2\cdot \left(10^{n+1}+\cdots+10^{1}\right)+5\,.[/tex]
Observando que temos as somas de duas Progressões Geométricas de razão [tex]10[/tex]:
[tex]\qquad\qquad \left(10^{n+2},\cdots,10^{2n+1}\right)[/tex] com [tex]n[/tex] termos e [tex]\left(10,\cdots,10^{n+1}\right)[/tex] com [tex]n+1[/tex] termos,
podemos utilizar a fórmula do Lembrete e continuar com nossos cálculos:
[tex]\qquad N=4\cdot \dfrac{10^{n+2}\cdot\left(10^n-1 \right)}{10-1}+2\cdot\dfrac{10 \cdot\left(10^{n+1}-1 \right)}{10-1}+5 \\
\qquad N=4\cdot \dfrac{\left(10^{2n+2}-10^{n+2} \right)}{9}+2\cdot\dfrac{\left(10^{n+2}-10 \right)}{9}+5 \\
\qquad N=\dfrac{1}{9} \cdot\left(4\cdot 10^{2n+2}-4\cdot 10^{n+2}+2\cdot 10^{n+2}\right)-\dfrac{20}{9}+5\\
\qquad N=\dfrac{1}{9} \cdot\left(4\cdot 10^{2n+2}-2\cdot 10^{n+2}\right)+\dfrac{25}{9}\\
\qquad N=\dfrac{1}{9} \cdot\left(4\cdot 10^{2n+2}-2\cdot 10^{n+2}+25\right)\\
\qquad N=\dfrac{1}{9} \cdot\left((2\cdot 10^{n+1})^2-2\cdot 10 \cdot 10^{n+1}+5^2\right)\\
\qquad N=\dfrac{1}{9} \cdot\left((2\cdot 10^{n+1})^2-2\cdot (2 \cdot 10^{n+1})\cdot 5+5^2\right)\\
\qquad N=\dfrac{1}{9} \cdot\left(2\cdot 10^{n+1}-5\right)^2\\
\qquad N=\left(\dfrac{2\cdot 10^{n+1}-5}{3}\right)^2\,.\\
[/tex]
Observe que como [tex]N[/tex] é um número natural, então [tex]x=\dfrac{2\cdot 10^{n+1}-5}{3}[/tex] é também um número natural; assim:
[tex]\qquad N=x^2[/tex], com [tex]x \in \mathbb{N}[/tex].
Portanto, para todo número natural [tex]n[/tex], o número da forma [tex]\; \underbrace{44\cdots 4}_{n}\underbrace{22 \cdots 2}_{n+1}5[/tex] é um quadrado perfeito!
Observação: Se você quiser provar que, de fato, [tex]x=\dfrac{2\cdot 10^{n+1}-5}{3}[/tex] é também um número natural, observe que:
|
[tex]\qquad 2\cdot 10^{n+1}=2\underbrace{0\cdots 0}_{n+1 \text{ zeros}}\\ \qquad 2\cdot 10^{n+1}-5=2\underbrace{0\cdots 0}_{n+1 \text{ zeros}}-5\\ \qquad 2\cdot 10^{n+1}-5=1\underbrace{9\cdots 9}_{n \text{ noves}}5\\[/tex] |
[tex] \begin{array}{c c c c c c l} |
Assim, a soma dos algarismos de [tex] 2\cdot 10^{n+1}-5[/tex] é:
[tex]\qquad S=1+\underbrace{9+9+\cdots+9}_{n \text{ parcelas } 9}+5\\
\qquad S=6+9\cdot n\\
\qquad S=3\cdot(2+3n)[/tex]
e, com isso, [tex]S[/tex] é um número natural divisível por [tex]3\,[/tex], já que [tex](2+3n) \in \mathbb{N}\,.[/tex]
Agora, lembre-se de que se a soma dos algarismos de um número natural for divisível por [tex]3[/tex], o próprio número é divisível por [tex]3[/tex]; assim, [tex] 2\cdot 10^{n+1}-5[/tex] é divisível por [tex]3[/tex] e, consequentemente, [tex]x=\dfrac{2\cdot 10^{n+1}-5}{3}[/tex] é um número natural.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
