Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 1º ano do E. M.- Nível de dificuldade: Difícil)
(ITA, 2010) Os conjuntos [tex]A \,[/tex] e [tex]\, B[/tex] são formados por números reais e [tex]C[/tex] é um subconjunto da união [tex]A \cup B[/tex].
Sabendo que [tex]A \cup B[/tex], [tex]A \cap C[/tex] e [tex]B \cap C[/tex] são os domínios das funções reais abaixo definidas
[tex]\qquad \begin{align*} f: \, & A \cup B \rightarrow \mathbb{R}\\ & f(x)= ln (x-\sqrt{\pi})\;;\end{align*}\\[/tex]
[tex]\qquad \begin{align*} g: \, &A \cap C \rightarrow \mathbb{R}\\ & g(x)=\sqrt{ -x^2 + 6x – 8 }\;;\end{align*}\\[/tex]
[tex]\qquad \begin{align*} h: \, &B \cap C \rightarrow \mathbb{R}\\ & h(x)=\sqrt{\dfrac{x-\pi}{5-x} }\;;\end{align*}[/tex]
determinar [tex]C[/tex].
Solução 1
Vamos inicialmente determinar os domínios das funções [tex]f,g,h.[/tex]
- O número real [tex]ln(t)[/tex] está definido apenas para valores positivos de [tex]t.[/tex]
- O número real [tex]\sqrt{t}[/tex] está definido apenas para valores não negativos de [tex]t.[/tex]
- Em um plano cartesiano [tex]xOy[/tex] o gráfico de [tex]l[/tex] é uma parábola com eixo de simetria paralelo ao eixo [tex]Oy[/tex] e concavidade voltada para cima. Para traçar esse gráfico e analisar a variação de sinal, vamos precisar das raízes da equação de segundo grau [tex]x^2 – 6x + 8=0[/tex]; são elas:
- Já vimos que o número real [tex]\sqrt{t}[/tex] está definido apenas para valores não negativos de [tex]t.[/tex]
- Em um plano cartesiano [tex]xOy[/tex] as equações [tex]y=x-\pi[/tex] e [tex]y=5-x[/tex] definem duas retas oblíquas, a primeira cortando o eixo [tex]Ox[/tex] em [tex]x=\pi[/tex] e a segunda em [tex]x=5.[/tex]
Veja um esboço do gráfico das duas retas:
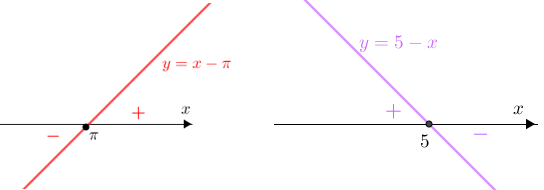
e o estudo da variação de sinal do quociente [tex]\dfrac{x-\pi}{5-x}[/tex]:
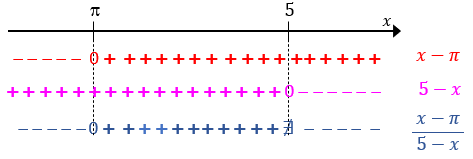
Dessa forma, para que [tex]\textcolor{#4472C4}{\sqrt{\dfrac{x-\pi}{5-x}}}[/tex] seja um número real, devemos ter [tex]\, \fcolorbox{black}{#d2ddf1}{$\pi\leqslant x\lt 5$}\,.[/tex] - [tex]\textcolor{#00B0F0}{A\cup B=d(f)=\left]\sqrt{\pi},+\infty \right[}[/tex];
- [tex]\textcolor{#00f}{A\cap C=d(g)=\left[2,4\right]}[/tex];
- [tex]\textcolor{#4472C4}{B\cap C=d(h)=\left[\pi,5\right[}[/tex].
Então, para que [tex]\textcolor{#00B0F0}{ln (x-\sqrt{\pi})}[/tex] seja um número real, devemos ter [tex] x-\sqrt{\pi} \gt 0[/tex], ou seja, [tex]\, \fcolorbox{black}{#bdedff}{$x\gt \sqrt{\pi}$}\,.[/tex]
Então, para que [tex]\sqrt{ -x^2 + 6x – 8 }[/tex] defina um número real, devemos ter [tex] -x^2 + 6x – 8 \geqslant 0[/tex], ou seja, [tex] x^2 – 6x + 8 \leqslant 0.[/tex] Para resolver essa desigualdade, vamos estudar a variação de sinal da função [tex]l(x)= x^2 – 6x + 8 .[/tex]
[tex]\qquad x=\dfrac{-(-6)\pm\sqrt{(-6)^2-4\cdot 1\cdot 8}}{2 \cdot 1}\\
\qquad x=\dfrac{6\pm\sqrt{36-32}}{2}\\
\qquad x=\dfrac{6\pm\sqrt{4}}{2} \\
\qquad x_1=\dfrac{6-2}{2}=2 \qquad \text{e}\qquad x_2=\dfrac{6+2}{2}=4\,. [/tex]
Veja um esboço do gráfico de [tex]l[/tex]:
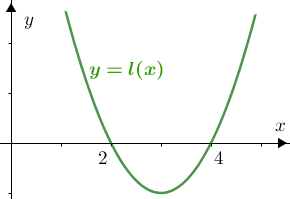
e sua variação de sinal:

Dessa forma, para que [tex]\textcolor{#00f}{\sqrt{ -x^2 + 6x – 8}}[/tex] seja um número real, devemos ter [tex]\, \fcolorbox{black}{#ccf}{$2\leqslant x\leqslant 4$}\,.[/tex]
Então, para que [tex]\sqrt{\dfrac{x-\pi}{5-x}}[/tex] defina um número real, devemos ter [tex]\dfrac{x-\pi}{5-x} \geqslant 0[/tex], desde que tenhamos [tex]x \ne 5.[/tex] Para resolver a desigualdade [tex]\dfrac{x-\pi}{5-x} \geqslant 0[/tex], vamos estudar a variação de sinal do numerador e do denominador da fração.
Pelo até aqui exposto, temos que:
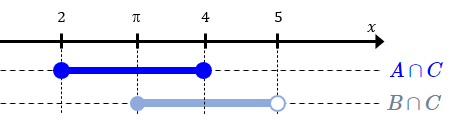
Agora, observe com atenção o diagrama abaixo.
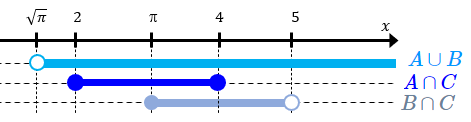
Como [tex]A \cap C \subset C\;[/tex] e [tex]\;B \cap C \subset C[/tex], então desse diagrama concluímos que [tex][2,5[ \subset C\,.[/tex]
Por outro lado, sabemos que [tex]C \subset A \cup B\;[/tex]. Mas se existisse um elemento [tex]z \in C [/tex] tal que [tex]z \;\in \left]\sqrt{\pi}, 2\right[ \cup [5,+\infty[ [/tex] esse elemento [tex]z[/tex] pertenceria a [tex]A \cap C\;[/tex] ou a [tex]\;B \cap C[/tex], o que observamos não acontecer.
Portanto, [tex]\, \fcolorbox{black}{#eee0e5}{$C=\left[2,5\right[$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Antes de fazermos contas, poderíamos ter observado que [tex]\boxed{C=(A\cap C)\cup (B\cap C)}[/tex].
Assim, nem precisaríamos de todos os cálculos feitos na solução anterior para obtermos o domínio da função [tex]f[/tex].
Neste caso, aproveitando alguns cálculos da Solução 1, observamos o diagrama abaixo para efetuarmos a união [tex]\boxed{(A\cap C)\cup (B\cap C)}[/tex] e concluirmos que [tex]\, \fcolorbox{black}{#eee0e5}{$C=\left[2,5\right[$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
