Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M.- Nível de dificuldade: Médio)
(IME, 2016 – Adaptado) Quantas soluções inteiras o sistema de inequações
[tex]\qquad \qquad \quad \quad \begin{cases}
x \leqslant 10\\
\,\\
\dfrac{x^2-2x-14}{3x} \gt 1
\end{cases}\\[/tex]
admite?

Lembretes
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,\, a\not=0[/tex], é uma parábola com eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
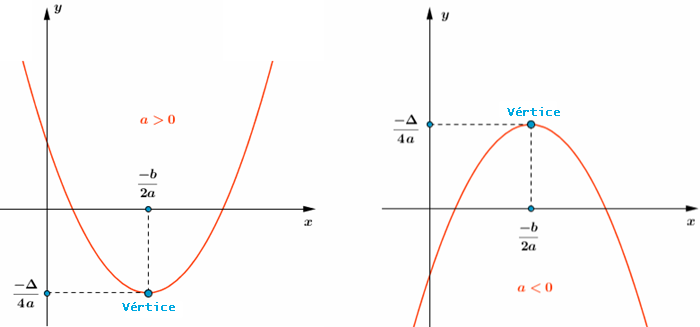
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola são dadas por [tex](x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex], sendo que [tex]x_v=\dfrac{-b}{2a}\, [/tex] e [tex]\, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
Solução
Observe, inicialmente, a seguinte sequência de desigualdades equivalentes:
[tex]\boxed{\dfrac{x^2-2x-14}{3x} \gt 1} \iff \dfrac{x^2-2x-14}{3x} -1 \gt 0 \iff \dfrac{x^2-2x-14}{3x} -\dfrac{3x}{3x} \gt 0 \iff \\
\iff \dfrac{x^2-5x-14}{3x} \gt 0 \iff \boxed{\dfrac{x^2-5x-14}{x} \gt 0}\,. [/tex]
Assim, para determinarmos os valores inteiros de [tex]x[/tex] que satisfazem o sistema
[tex]\begin{cases}
x \leqslant 10\\
\,\\
\dfrac{x^2-2x-14}{3x} \gt 1
\end{cases}\\[/tex]
determinaremos os valores inteiros de [tex]x[/tex] que satisfazem a desigualdade [tex]\dfrac{x^2-5x-14}{x} \gt 0 [/tex] e verificaremos quais desses valores satisfazem a condição [tex]x \leqslant 10.[/tex]
Para determinar os valores de [tex]x[/tex] para os quais a expressão é positiva, vamos estudar a variação de sinal da expressão [tex]\dfrac{x^2-5x-14}{x}\,.[/tex]
Para isso, inicialmente faremos um esboço dos gráficos das funções [tex]f,\,g:\mathbb{R}\rightarrow \mathbb{R}[/tex] definidas por [tex]f(x)=x^2-5x-14[/tex] e [tex]g(x)=x[/tex] e analisaremos o sinal de cada uma.
Lembramos que analisar o sinal de uma função significa determinar quais valores do seu domínio têm imagens iguais a zero, quais têm imagens positivas e quais têm imagens negativas.
Vamos lá!
- Em um plano cartesiano [tex]xOy[/tex] o gráfico de [tex]f[/tex] é uma parábola com eixo de simetria paralelo ao eixo [tex]Oy[/tex] e concavidade voltada para cima. Para traçar esse gráfico e analisar a variação de sinal, vamos precisar das raízes da equação de segundo grau [tex]x^2-5x-14=0[/tex]; são elas:
- Em um plano cartesiano [tex]xOy[/tex] o gráfico de [tex]g[/tex] é uma reta que passa pela origem e pelo ponto de coordenadas [tex](2,2)[/tex], por exemplo.
[tex]\qquad x=\dfrac{-(-5)\pm\sqrt{(-5)^2-4\cdot 1\cdot (-14)}}{2 \cdot 1}\\
\qquad x=\dfrac{5\pm\sqrt{25+56}}{2}\\
\qquad x=\dfrac{5\pm\sqrt{81}}{2} \\
\qquad x_1=\dfrac{5-9}{2}=-2 \qquad \text{e}\qquad x_2=\dfrac{5+9}{2}=7\,. [/tex]
Veja um esboço do gráfico de [tex]f[/tex]:
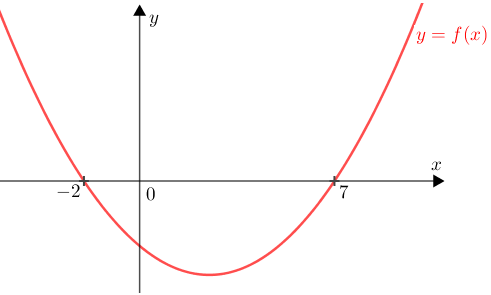
e sua variação de sinal:

Assim, temos um esboço do gráfico de [tex]g[/tex]:
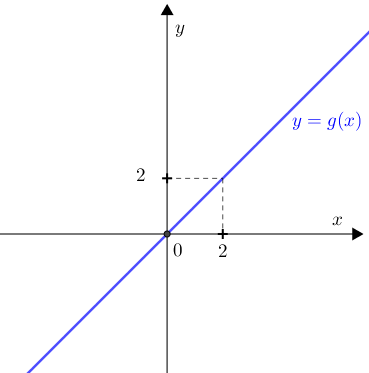
e sua variação de sinal:

Temos então o seguinte quadro final com a variação de sinais da [tex]f[/tex], da [tex]g[/tex] e da [tex]\dfrac{f}{g}[/tex] :
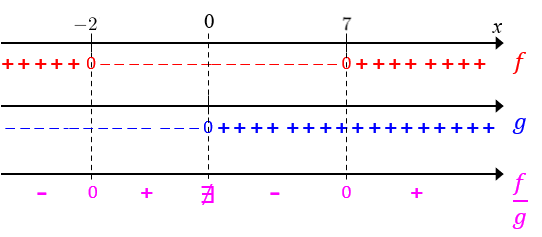
Portanto, os valores reais de [tex]x[/tex] que satisfazem a inequação [tex]\dfrac{x^2-5x-14}{x} \gt 0 [/tex] são tais que [tex]–2 \lt x \lt 0[/tex] ou [tex]x \gt 7[/tex].
Dentre esses números reais, são inteiros e menores do que ou iguais a [tex] 10 [/tex] os seguintes valores: [tex] –1,\, 8, \, 9 \,[/tex] e [tex]\,10[/tex].
Assim, o sistema de inequações apresentado no problema tem [tex] \, \fcolorbox{black}{#eee0e5}{$\, 4$}\,[/tex] soluções inteiras.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
