Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Difícil)
Em um papel quadriculado, foi desenhado um quadrado com [tex]4\, \text{cm}[/tex] de lado, conforme mostra a figura.
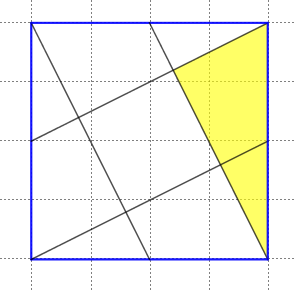
Determine a medida da área colorida de amarelo.
AJUDAS
(1) Caso de congruência L.A.L. (lado – ângulo – lado): Se dois triângulos têm ordenadamente congruentes dois lados e o ângulo por eles definido, então estes triângulos são congruentes.
(Se você não se lembra desse resultado, clique AQUI.)
(2) Caso de Semelhança A.A. (ângulo – ângulo): Se dois ângulos de um triângulo são congruentes a dois ângulos de outro triângulo, então estes triângulos são semelhantes.
(3) Em triângulos semelhantes, os lados correspondentes são proporcionais.
(Há uma Sala de Ajuda sobre triângulos semelhantes no nosso Blog!)
(4) Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
Solução
Para facilitar a solução, vamos nomear alguns pontos que aparecem na figura original do problema.
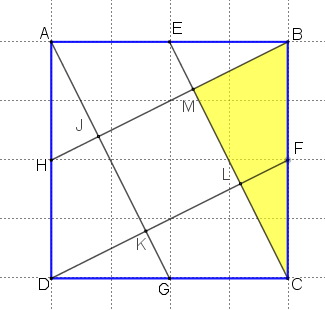
Conforme mostra a figura do problema, a medida [tex]S_{am}[/tex] da área colorida de amarelo é a diferença entre a medida [tex]S_{1}[/tex] da área do triângulo [tex]CBE[/tex] e a medida [tex]S_{2}[/tex] da área do triângulo [tex]MEB[/tex]. Dessa forma, precisamos determinar [tex]S_{1}[/tex] e [tex]S_{2}[/tex].
- Como o triângulo [tex]CBE[/tex] é um triângulo retângulo, a medida de sua área é o semiproduto entre as medidas de seus catetos. Sendo [tex]E[/tex] o ponto médio do lado [tex]AB[/tex] do quadrado, segue que:
- O cálculo de [tex]S_2[/tex] não é tão imediato!
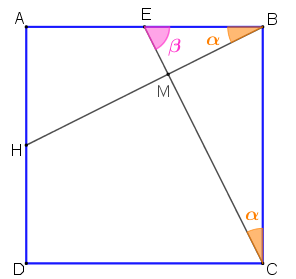Observe inicialmente que os pontos [tex]E[/tex] e [tex]H[/tex] são pontos médios dos lados [tex]AB[/tex] e [tex]AD[/tex], respectivamente. Como os triângulos [tex]BAH[/tex] e [tex]CBE[/tex] são retângulos, então pelo Lembrete (1) esses triângulos são congruentes. Assim, os ângulos [tex]B\widehat{C}E[/tex] e [tex]A\widehat{B}H[/tex] têm a mesma medida, digamos [tex]\textcolor{#FF7F00}{\alpha}[/tex].
Note que o ângulo [tex]M\widehat{E}B[/tex], cuja medida estamos denotando por [tex]\textcolor{#FF33CC}{\beta}[/tex], é comum aos triângulos [tex]MEB[/tex] e [tex]CBE[/tex]; logo, pelo Lembrete (2) esses triângulos são semelhantes e, portanto, [tex]MEB[/tex] é um triângulo retângulo.
Sendo um triângulo retângulo, a medida da área do triângulo [tex]MEB[/tex] é o semiproduto entre as medidas de seus catetos. Vamos denotar por [tex]a[/tex] e [tex]b[/tex] o comprimento em centímetros dos catetos [tex]MB[/tex] e [tex]ME[/tex], respectivamente, e calcular essas medidas.
Mas antes, vamos aplicar o Teorema de Pitágoras para determinar o comprimento [tex]h[/tex] da hipotenusa do triângulo [tex]CBE[/tex]:
[tex]\qquad h^2=4^2+2^2=16+4=20[/tex]
[tex]\qquad h=\pm \sqrt{20}=\pm 2\sqrt{5}[/tex].
Como [tex]h[/tex] é uma medida de comprimento, então [tex]h=2\sqrt{5}\,\text{cm}[/tex].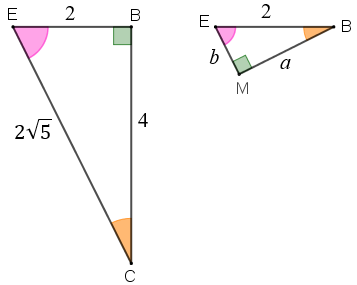
Observando os triângulos semelhantes [tex]CBE[/tex] e [tex]MEB[/tex], percebemos que, pelo Lembrete (3):
[tex] \qquad \dfrac{4}{a}=\dfrac{2}{b}=\dfrac{2\sqrt{5}}{2}=\sqrt{5}.[/tex]
Com isso, obtemos que:
[tex]\qquad a=\dfrac{4}{\sqrt{5}}\,\text{cm}\quad [/tex] e [tex]\quad b=\dfrac{2}{\sqrt{5}}\,\text{cm}[/tex],
donde:
[tex]\qquad S_2=\dfrac{\dfrac{4}{\sqrt{5}}\times \dfrac{2}{\sqrt{5}}}{2}=\dfrac{\dfrac{8}{5}}{2} [/tex]
[tex]\qquad S_2=\boxed{\dfrac{4}{5}\, \text{cm}^2}. \qquad \textcolor{#800000}{(ii)} [/tex]
[tex]\qquad S_{1}=\dfrac{4 \times 2}{2}=\boxed{4\,\text{cm}^2}.\qquad \textcolor{#800000}{(i)}[/tex]
Finalmente, por [tex] \textcolor{#800000}{(i)}\,[/tex] e [tex]\, \textcolor{#800000}{(ii)} [/tex] segue que:
[tex]\qquad S_{am}=S_1-S_2[/tex]
[tex]\qquad S_{am}=4-\dfrac{4}{5}= \dfrac{16}{5}\,\text{cm}^2[/tex].
Portanto, a medida da área colorida de amarelo é [tex]\fcolorbox{black}{#eee0e5}{$3,2\,\text{cm}^2$}\,. [/tex]
Solução elaborada pelos Moderadores do Blog.
|
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |