Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 1º ano do E. M. – Nível de dificuldade: Médio)
(ONEM, 2011) O sistema
[tex]\qquad \qquad \begin{cases}
3ax+2by=16\\
x+2y=8
\end{cases}\\
\,[/tex]
tem infinitas soluções para as variáveis [tex]x[/tex] e [tex]y.[/tex]
Determinar os possíveis valores de [tex]a[/tex] e de [tex]b.[/tex]
Solução 1
Da segunda equação que compõe o sistema, obtemos que [tex] 2y=8-x[/tex] e substituindo essa expressão na primeira equação segue que
[tex]\quad 3ax+b\left(8-x \right)=16[/tex]
[tex]\quad 3ax+8b-bx =16[/tex]
[tex]\quad \left(3a-b\right)x+8b=16[/tex]
[tex]\quad \left(3a-b\right)x=16-8b. \qquad \textcolor{#800000}{(i)}[/tex]
Perceba que se [tex]3a-b \ne 0[/tex], concluiríamos de [tex]\textcolor{#800000}{(i)}[/tex] que [tex]x=\dfrac{16-8b}{3a-b}[/tex] e, portanto, [tex]x[/tex] teria um único valor, o que contradiz a hipótese de que a variável [tex]x[/tex] tem infinitos valores.
Dessa forma, [tex]3a-b=0[/tex] e, por [tex]\textcolor{#800000}{(i)}[/tex], segue que [tex]16-8b=0 [/tex] e, então, [tex]\fcolorbox{black}{#eee0e5}{$b=2$}\,. [/tex]
Como [tex]3a-b=0[/tex] e [tex]b=2[/tex], temos que [tex]\fcolorbox{black}{#eee0e5}{$a=\dfrac{2}{3}$}\,. [/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Observe que se [tex]b= 0[/tex], segue da primeira equação do sistema que [tex]3ax=16[/tex]. Então:
- Se [tex]a=0[/tex], teríamos [tex]0=16[/tex], o que é um absurdo.
- Se [tex]a\ne 0[/tex], teríamos [tex]x=\dfrac{16}{3a}[/tex], o que contrariaria a hipótese de que o sistema tem infinitas soluções.
Dessa forma, [tex]b\ne 0[/tex] e consequentemente o sistema dado no problema é equivalente ao sistema
[tex]\qquad \qquad S_1:\begin{cases}
y=-\dfrac{3a}{2b}x+\dfrac{8}{b}\\
y=-\dfrac{1}{2}x+4
\end{cases}\\
\,\;\;\;[/tex].
Em um plano cartesiano [tex]xOy[/tex], as duas equações desse novo sistema representam um par de retas e sabemos que existem três posições relativas de duas retas coplanares:
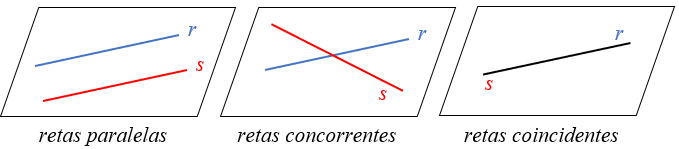
Sabemos também que:
- retas paralelas (distintas) não têm pontos de interseção;
- retas concorrentes têm um único ponto de interseção;
- retas coincidentes têm infinitos pontos de interseção.
Assim, como as soluções [tex]x\,[/tex] e [tex]\,y[/tex] do sistema [tex]S_1[/tex] são as coordenadas dos pontos do plano cartesiano que pertencem às duas retas, com a hipótese de que o sistema original, e consequentemente [tex]S_1[/tex], tem infinitas soluções para [tex]x\,[/tex] e [tex]\,y[/tex] concluímos que as retas definidas pelas equações de [tex]S_1[/tex] são coincidentes. Dessa forma, essas retas têm os mesmos coeficientes angulares e os mesmos coeficientes lineares
[tex]\qquad \qquad y=\textcolor{red}{-\dfrac{3a}{2b}}x+\textcolor{blue}{\dfrac{8}{b}} \qquad ; \qquad y=\textcolor{red}{-\dfrac{1}{2}}x+\textcolor{blue}{4}[/tex].
Logo:
[tex]\qquad \qquad -\dfrac{3a}{2b}=-\dfrac{1}{2}\quad [/tex] e [tex]\qquad \dfrac{8}{b}=4[/tex].
Da segunda igualdade, segue que [tex]\,\fcolorbox{black}{#eee0e5}{$b=2$}\,. [/tex] Substituindo esse valor na primeira equação, temos que [tex]\dfrac{3a}{2\cdot 2}=\dfrac{1}{2}[/tex], donde segue que [tex]\fcolorbox{black}{#eee0e5}{$a=\dfrac{2}{3}$}\,. [/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
