Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 7º ano do E. F. – Nível de dificuldade: Médio)
Ao colocar uma bomba de retirar água no galão de sua casa, dona Teresa não percebeu que a bomba estava com defeito e, durante quatro horas, toda a água do galão foi derramada…

Sabemos que, ao término de cada uma hora de vazamento, a água que saiu do galão foi "a metade da água que havia no início da hora mais meio litro". Quantos litros de água foram derramados?
Solução
Vamos fazer dois esqueminhas para ajudar na solução deste problema.
- Suponha, inicialmente, que [tex]q[/tex] seja a quantidade de litros de água do galão da casa da dona Teresa em um determinado instante. Quantos litros de água estarão no galão daqui a uma hora?
Seja [tex]f[/tex] essa quantidade; assim, [tex]f[/tex] é a diferença entre [tex]q[/tex] e a quantidade de água derramada em uma hora.
Sabemos que a água que sai do galão em uma hora é "a metade da água que havia no início da hora mais meio litro", logo: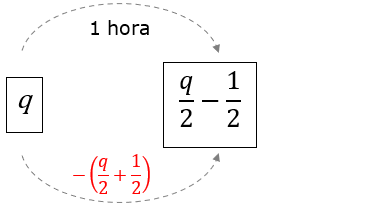
[tex]\qquad f=q-\left(\dfrac{q}{2}+\dfrac{1}{2} \right)\\
\qquad f=q-\dfrac{q}{2}-\dfrac{1}{2}\\
\qquad f=\left(q-\dfrac{q}{2}\right)-\dfrac{1}{2}\\
\qquad \boxed{f=\dfrac{q}{2}-\dfrac{1}{2}}\,.[/tex] - Suponha, agora, que você conheça a quantidade [tex]f[/tex] de litros de água que restou no galão da casa da dona Teresa após uma hora de vazamento e que você precise determinar a quantidade [tex]q[/tex] de litros de água no galão antes do vazamento.
Como [tex]f=\dfrac{q}{2}-\dfrac{1}{2}[/tex], segue que:
[tex]\qquad 2f=q-1\\
\qquad \boxed{q=2f+1}\,. [/tex]
Veja os dois esqueminhas!
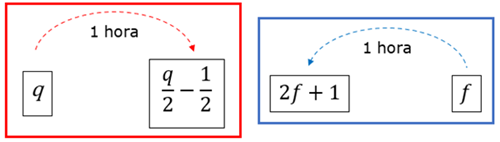
[tex]\textcolor{#800000}{(1)}[/tex] Utilizando o primeiro esquema, se [tex]A[/tex] era a quantidade de litros de água no galão após Teresa colocar a bomba, segue que:
[tex]\boxed{A}\, \xrightarrow{\text{1 hora}}\, \boxed{\dfrac{A}{2}-\dfrac{1}{2}}\, \xrightarrow{\text{1 hora}}\,\dfrac{\dfrac{A}{2}-\dfrac{1}{2}}{2}-\dfrac{1}{2}[/tex].
Como [tex]\, \dfrac{\dfrac{A}{2}-\dfrac{1}{2}}{2}-\dfrac{1}{2}=\dfrac{A}{4}-\dfrac{1}{4}-\dfrac{1}{2}=\boxed{\dfrac{A}{4}-\dfrac{3}{4}}\,[/tex], o esquema de esvaziamento do galão após três horas segue assim:
[tex]\boxed{A}\, \xrightarrow{\text{1 hora}}\, \boxed{\dfrac{A}{2}-\dfrac{1}{2}}\, \xrightarrow{\text{1 hora}}\, \boxed{\dfrac{A}{4}-\dfrac{3}{4}}\, \xrightarrow{\text{1 hora}}\, \dfrac{\dfrac{A}{4}-\dfrac{3}{4}}{2}-\dfrac{1}{2}[/tex].
Calculando agora [tex]\, \dfrac{\dfrac{A}{4}-\dfrac{3}{4}}{2}-\dfrac{1}{2}=\dfrac{A}{8}-\dfrac{3}{8}-\dfrac{1}{2}=\boxed{\dfrac{A}{8}-\dfrac{7}{8}}\,[/tex], o esquema de esvaziamento do galão após quatro horas fica assim:
[tex]\boxed{A}\, \xrightarrow{\text{1 hora}}\, \boxed{\dfrac{A}{2}-\dfrac{1}{2}}\, \xrightarrow{\text{1 hora}}\, \boxed{\dfrac{A}{4}-\dfrac{3}{4}}\, \xrightarrow{\text{1 hora}}\, \boxed{\dfrac{A}{8}-\dfrac{7}{8}}\, \xrightarrow{\text{1 hora}}\, \dfrac{\dfrac{A}{8}-\dfrac{7}{8}}{2}-\dfrac{1}{2}[/tex].
Como [tex]\, \dfrac{\dfrac{A}{8}-\dfrac{7}{8}}{2}-\dfrac{1}{2}=\dfrac{A}{16}-\dfrac{7}{16}-\dfrac{1}{2}=\boxed{\dfrac{A}{16}-\dfrac{15}{16}}\,[/tex] e após quatro horas o galão ficou vazio, o esquema de esvaziamento do galão finaliza desta forma:
[tex]\boxed{A}\, \xrightarrow{\text{1 hora}}\, \boxed{\dfrac{A}{2}-\dfrac{1}{2}}\, \xrightarrow{\text{1 hora}}\, \boxed{\dfrac{A}{4}-\dfrac{3}{4}}\, \xrightarrow{\text{1 hora}}\, \boxed{\dfrac{A}{8}-\dfrac{7}{8}}\, \xrightarrow{\text{1 hora}}\, \boxed{\dfrac{A}{16}-\dfrac{15}{16}}=0[/tex].
De [tex]\dfrac{A}{16}-\dfrac{15}{16}=0[/tex], concluímos que [tex]A=15[/tex]. Portanto, foram derramados [tex] \, \fcolorbox{black}{#eee0e5}{$ 15 \text{ litros}\,$}[/tex] de água.
[tex]\textcolor{#800000}{(2)}[/tex] Utilizando o segundo esquema, se [tex]0[/tex] foi a quantidade de litros de água no galão após quatro horas de vazamento, segue que:
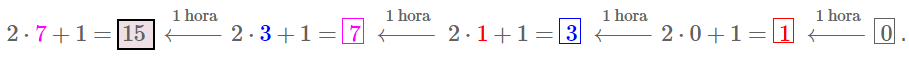
Portanto, foram derramados [tex] \, \fcolorbox{black}{#eee0e5}{$ 15 \text{ litros}\,$}[/tex] de água.
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
