Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Medio)
Dado o conjunto
- [tex]A = \{1, 2, 3, 4, 5, 6, 8, 9, 11, 12, 13, 14, 15, 17, 18, 19, 20\}[/tex],
quantos subconjuntos com três elementos podem ser formados de maneira que a soma dos três elementos seja um número par?

Ajuda
✏ Combinação simples: Uma das maneiras de agruparmos elementos de um dado conjunto é escolhê-los levando-se em consideração apenas a sua natureza, sem se importar em que ordem eles foram escolhidos ou apresentados. Esse tipo de agrupamento de elementos é denominado uma Combinação simples. Particularmente, quando escolhemos [tex]r[/tex] dentre [tex]n[/tex] elementos de um conjunto dessa forma, dizemos que estamos definindo uma Combinação simples de [tex]n[/tex] elementos tomados [tex]r[/tex] a [tex]r[/tex]. A quantidade desse tipo de agrupamentos é denotada por [tex]C_{n,r}[/tex] ou [tex]C_n^r\,[/tex] e assim definida:
[tex]C_{n,r}=C_n^r=\dfrac{n!}{(n-r)!\,r!} \text{, com } n,r\in\mathbb{N^*} \text{ e } r\leqslant n[/tex].
✏ Princípio Fundamental da Contagem, ou Princípio Multiplicativo, para duas decisões:
Se uma decisão A pode ser tomada de [tex] m [/tex] maneiras distintas e, tomada essa decisão A, uma decisão B puder ser tomada de [tex] n [/tex] maneiras distintas, então a quantidade de maneiras de se tomar sucessivamente as decisões A e B é igual a [tex]~\boxed{ m \times n}\, . [/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
✏ Princípio Aditivo, para duas decisões: Se
- uma decisão D1 puder ser tomada de [tex] m_1 [/tex] maneiras distintas,
- uma decisão D2 puder ser tomada de [tex] m_2 [/tex] maneiras distintas e
- essas decisões forem independentes entre si (isto é, a escolha de uma não muda a quantidade de possibilidades para a escolha da outra),
então a quantidade de maneiras em que as duas decisões podem ser tomadas uma de cada vez é
[tex]\qquad \qquad \boxed{m_1+ m_2 }\, .[/tex]
Solução
Sabemos que a paridade da soma no conjunto dos números naturais é definida de acordo com a tabela abaixo.
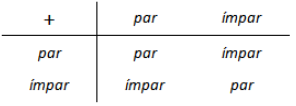
Assim, para que a soma de três números naturais seja um número par uma das seguintes situações deve ocorrer:
- os três números são pares ([tex]par+par+par=par[/tex]);
- dois números são ímpares e o outro é par ([tex]ímpar+ímpar+par=par[/tex]).
Dessa forma, os subconjuntos considerados no enunciado podem ser definidos de duas maneiras independentes. Vamos contar separadamente a quantidade de subconjuntos de cada tipo:
- ► Subconjuntos formados por três números pares
Neste caso, vamos escolher [tex]3[/tex] dentre os [tex]8[/tex] elementos do conjunto [tex]A[/tex], sem nos importarmos com a ordem em que eles serão escolhidos. A quantidade [tex]m_1[/tex] de escolhas que podemos fazer é, portanto, uma Combinação Simples de [tex]8[/tex] elementos tomados [tex]3[/tex] a [tex]3[/tex]:
[tex]\qquad \qquad m_1=C_8^3=\dfrac{8!}{(8-3)!\,3!}=\dfrac{8!}{5!\,3!}=\dfrac{8 \times 7 \times 6} {3 \times 2 \times 1}[/tex]
[tex]\qquad \qquad \boxed{m_1=56}\,.[/tex]
► Subconjuntos formados por dois números ímpares e um par
Vamos escolher [tex]2[/tex] dentre os [tex]9[/tex] ímpares do conjunto [tex]A[/tex], sem nos importarmos com a ordem em que eles serão escolhidos; assim, a quantidade dessas escolhas é dada por:
[tex]\qquad \qquad C_9^2=\dfrac{9!}{(9-2)!\,2!}=\dfrac{9!}{7!\,2!}=\dfrac{9 \times 8 } { 2 \times 1}=36.[/tex]
Como a escolha do único par pode ser feita de [tex]8[/tex] maneiras, o Princípio Multiplicativo nos garante que a quantidade [tex]m_2[/tex] de escolhas simultâneas de dois ímpares e um único par é:
[tex]\qquad \qquad \boxed{m_2=36 \times 8=288}\,.[/tex]
Finalmente, o Princípio Aditivo nos assegura que a quantidade [tex] M[/tex] de subconjuntos de [tex]M[/tex] com três elementos cuja soma seja um número par é dada por:
[tex]\qquad \qquad M=m_1+m_2[/tex]
[tex]\qquad \qquad M=56+288[/tex]
[tex]\qquad \qquad \fcolorbox{black}{#eee0e5}{$M=344$}\,. [/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
