Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 7º ano do E. F. – Nível de dificuldade: Médio)
Para saldar uma pequena dívida, o pintor Brubério decidiu “fazer um bico” no próximo fim de semana. Como ele é um excelente profissional, não faltaram ofertas de trabalho e ele está decidindo entre duas:
- pintar a frente do muro da casa da dona Odete ou pintar a frente do muro da casa do seu Júlio, ganhando a mesma quantia em reais em ambos os serviços.
O muro da dona Odete tem base [tex]30\%[/tex] maior que a base do muro do seu Júlio, mas tem altura [tex]30\%[/tex] menor que a altura do muro do seu Júlio.
Assim, qual a melhor escolha que Brubério pode fazer?

Ajuda
Se você tem dificuldades com cálculos de porcentagem, dê uma passadinha nesta Sala, antes de ler a solução!
Solução
Vamos basear a nossa solução nas medidas do muro do seu Júlio; assim suponhamos que a medida da base do muro seja [tex]b\, metros[/tex] e a sua altura seja [tex]a\, metros[/tex], conforme ilustrado na figura a seguir.
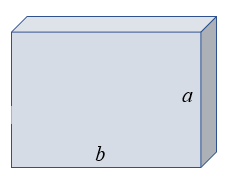
Como o muro da dona Odete tem base [tex]30\%[/tex] maior que a base do muro do seu Júlio e altura [tex]30\%[/tex] menor, as medidas do muro da dona Odete são:
- base: [tex]\quad b+30\%\,b=b+\frac{30}{100}b=b+\frac{3}{10}b=b+0,3b=1,3b\,[/tex];
- altura: [tex]\quad a-30\%\,a=a-\frac{30}{100}a=a-\frac{3}{10}a=a-0,3a=0,7a\,.[/tex]

Dessa forma, as áreas [tex]A_O[/tex] e [tex]A_J[/tex] dos muros da dona Odete e do seu Júlio a serem pintadas são dadas por:
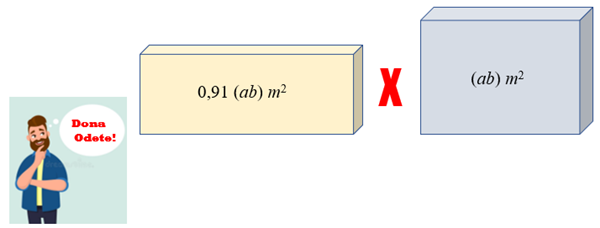
[tex]\qquad A_O=\text{base} \times \text{altura}=1,3b \times 0,7a=0,91\left(ab\right)\,m^2[/tex];
[tex]\qquad A_J=\text{base} \times \text{altura}=b \times a=\left(ab\right)\,m^2[/tex].
Como [tex]\, \fcolorbox{black}{#eee0e5}{$A_O \lt A_J$}\, [/tex], será mais vantajoso para o Brubério pintar o muro da dona Odete!
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
