Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
Embora os números naturais [tex]x [/tex] e [tex]y [/tex] não sejam múltiplos de [tex]10 [/tex], o produto entre eles é uma potência de [tex]10. [/tex]
Se [tex]x \gt y [/tex], que algarismo ímpar NÃO pode ser o dígito das unidades da diferença [tex]x-y \,[/tex]?
Solução 1
Sejam [tex]x [/tex] e [tex]y [/tex] números naturais não múltiplos de [tex]10 [/tex] tais que
[tex]\qquad \qquad x\cdot y=10^n[/tex], com [tex]n[/tex] um número natural não nulo.
Dessa forma, os únicos números primos que entram na decomposição dos números [tex]x [/tex] e [tex]y [/tex] são o [tex]2[/tex] e o [tex]5.[/tex] Mas perceba que tanto [tex]x [/tex] e [tex]y [/tex] não podem ter simultaneamente fatores [tex]2[/tex] e [tex]5[/tex] em suas decomposições, pois, se assim o fosse, eles seriam múltiplos de [tex]10.[/tex]
Com isso [tex]x [/tex] e [tex]y [/tex] são da forma [tex]2^n[/tex] e [tex]5^n[/tex] e como [tex]x \gt y [/tex], então [tex]\boxed{y=2^n}[/tex] e [tex]\boxed{x=5^n}.[/tex]
Particularmente, veja que:
- Se [tex]n=1[/tex], então [tex]y=2^1=2[/tex], [tex]x=5^1=5[/tex] e, portanto, [tex]x-y=\textcolor{red}{3}.[/tex]
- Se [tex]n=2[/tex], então [tex]y=2^2=4[/tex], [tex]x=5^2=25[/tex] e, portanto, [tex]x-y=2\textcolor{red}{1}.[/tex]
- Se [tex]n=3[/tex], então [tex]y=2^3=8[/tex], [tex]x=5^3=125[/tex] e, portanto, [tex]x-y=11\textcolor{red}{7}.[/tex]
- Se [tex]n=4[/tex], então [tex]y=2^4=16[/tex], [tex]x=5^4=625[/tex] e, portanto, [tex]x-y=60\textcolor{red}{9}.[/tex]
A partir desses exemplos já vemos que o dígito das unidades da diferença [tex]x-y[/tex] pode ser [tex]1,3,7[/tex] ou [tex]9.[/tex] Assim, o único candidato a NÃO ser o dígito das unidades da diferença [tex]x-y[/tex] é o [tex]5[/tex].
Vamos mostrar que isso realmente ocorre!
Com efeito, observe que se o dígito das unidades da diferença [tex]x-y[/tex] fosse [tex]5[/tex], [tex]x-y[/tex] seria um múltiplo de [tex]5[/tex]. Nesse caso, como [tex]x=5^n[/tex] é um múltiplo de [tex]5[/tex], então [tex]y[/tex] necessariamente seria um múltiplo de [tex]5[/tex], o que é impossível, visto que [tex]y=2^n[/tex] é uma potência de [tex]2.[/tex]
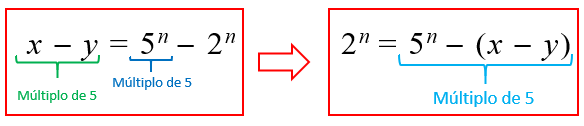
Pelo exposto, o dígito das unidades da diferença [tex]x-y\,\,[/tex] NÃO pode ser [tex] \, \fcolorbox{black}{#eee0e5}{$5$}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Sejam [tex]x [/tex] e [tex]y [/tex] números naturais não múltiplos de [tex]10 [/tex] tais que
[tex]\qquad \qquad x\cdot y=10^n[/tex], com [tex]n[/tex] um número natural não nulo.
Dessa forma, os únicos números primos que entram na decomposição dos números [tex]x [/tex] e [tex]y [/tex] são o [tex]2[/tex] e o [tex]5.[/tex] Mas perceba que [tex]x [/tex] e [tex]y [/tex] não podem ter simultaneamente fatores [tex]2[/tex] e [tex]5[/tex] em suas decomposições, pois, se assim o fosse, eles seriam múltiplos de [tex]10.[/tex]
Com isso, [tex]x [/tex] e [tex]y [/tex] são da forma [tex]2^n[/tex] e [tex]5^n[/tex] e como [tex]x \gt y [/tex], então [tex]\boxed{y=2^n}[/tex] e [tex]\boxed{x=5^n}.[/tex]
Agora, observe que:
- Como qualquer potência de [tex]5[/tex] termina em [tex]5[/tex], então o último dígito do [tex]x[/tex] é [tex]5.\qquad \textcolor{#800000}{(i)}[/tex]
- Vamos observar o último dígito das potências de [tex]2[/tex]:
[tex]\begin{array}{l l l l}
2^1=\textcolor{red}{2} \quad\quad & 2^5=3\textcolor{red}{2} \quad\quad& 2^9=51\textcolor{red}{2} \quad\quad & 2^{13}=819\textcolor{red}{2}\,\,\dots\\
2^2=\textcolor{red}{4} & 2^6=6\textcolor{red}{4} &2^{10}=102\textcolor{red}{4}&2^{14}=1638\textcolor{red}{4}\,\,\dots\\
2^3=\textcolor{red}{8} & 2^7=12\textcolor{red}{8} & 2^{11}=204\textcolor{red}{8} & 2^{15}=3276\textcolor{red}{8}\,\,\dots\\
2^4=1\textcolor{red}{6} & 2^8=25\textcolor{red}{6} & 2^{12}=409\textcolor{red}{6} & 2^{16}=6553\textcolor{red}{6} \,\, \dots\end{array}[/tex]
Perceba que ciclicamente as potências de [tex]2[/tex] terminam em [tex]\textcolor{red}{2},\textcolor{red}{4},\textcolor{red}{8}[/tex] e [tex]\textcolor{red}{6}.\qquad \textcolor{#800000}{(ii)}[/tex]
Com base nas conclusões [tex]\textcolor{#800000}{(i)}[/tex] e [tex]\textcolor{#800000}{(ii)}[/tex], vamos esquematizar as quatro situações possíveis para a diferença [tex]x-y:[/tex]
[tex]\begin{array}{l l}
a\,\cdots\, b & 5\\
c\,\cdots \, d & 2\\
\hline \
e\,\cdots \, f & \textcolor{red}{3} \end{array}-[/tex] [tex]\quad \begin{array}{l l}
a\,\cdots\, b & 5\\
c\,\cdots \, d & 4\\
\hline \
e\,\cdots \, f & \textcolor{red}{1} \end{array}-[/tex] [tex]\quad \begin{array}{l l}
a\,\cdots\, b & ^15\\
c\,\cdots \, d & 8\\
\hline \
e\,\cdots \, f & \textcolor{red}{7} \end{array}-[/tex] [tex]\quad \begin{array}{l l}
a\,\cdots\, b & ^15\\
c\,\cdots \, d & 6\\
\hline \
e\,\cdots \, f & \textcolor{red}{9} \end{array}-[/tex]
Observando os esqueminhas, vemos que o único algarismo ímpar que NÃO pode ser o dígito das unidades da diferença [tex]\, x−y[/tex] é o [tex] \, \fcolorbox{black}{#eee0e5}{$5$}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
