Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 7º ano do E. F. – Nível de dificuldade: Médio)
(XXIV OPM – 2005) Todos os triângulos da figura abaixo são equiláteros, sendo que o perímetro do triângulo maior é [tex]180\, cm[/tex].
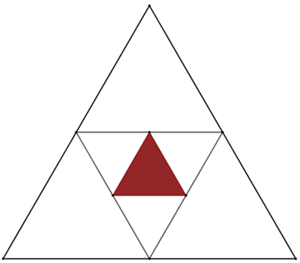
Qual é o perímetro do triângulo colorido?
Solução
► Como o triângulo [tex]GHI[/tex] é equilátero, os segmentos [tex]GH[/tex], [tex]HI[/tex] e [tex]IG[/tex] têm o mesmo comprimento, digamos [tex]\textcolor{red}{a}.[/tex]
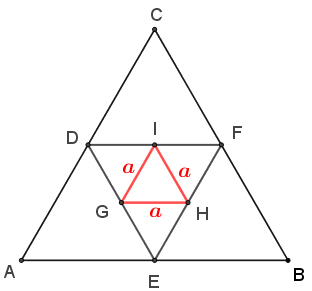
► Os triângulos [tex]DGI[/tex], [tex]GEH[/tex] e [tex]HFI[/tex] também são equiláteros; como cada um tem um lado com comprimento [tex]\textcolor{red}{a}[/tex], então os demais lados desses três triângulos têm comprimento [tex]\textcolor{red}{a}.[/tex]
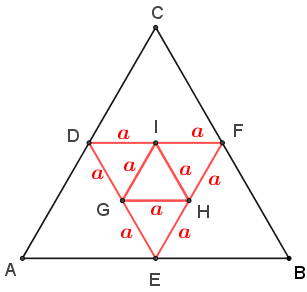
► Os triângulos [tex]AED[/tex], [tex]EBF[/tex] e [tex]DFC[/tex] são equiláteros; como cada um tem um lado com comprimento [tex]\textcolor{blue}{2a}[/tex], então os demais lados desses triângulos também têm comprimento [tex]\textcolor{blue}{2a}.[/tex]
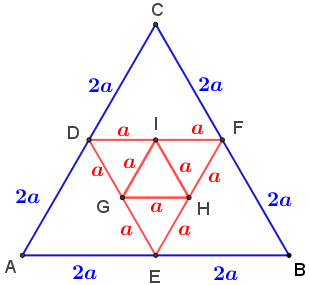
Pelo exposto, o triângulo [tex]ABC[/tex] tem lados que medem [tex]4a[/tex]; assim, o perímetro desse triângulo é [tex]4a+4a+4a=12a.[/tex] Mas, pelos dados do problema, esse perímetro é [tex]180\, cm[/tex], logo:
[tex]\qquad 12a=180 \, cm\\
\qquad a=15 \, cm.[/tex]
O triângulo colorido é o triângulo [tex]GHI[/tex]; portanto, o seu perímetro é [tex]a+a+a=3a[/tex], ou seja, [tex] \, \fcolorbox{black}{#eee0e5}{$45 \, cm$} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
