Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
Para evitar invasões de animais silvestres em suas plantações, um pequeno agricultor resolveu cercar o terreno retangular onde fica a sua horta, utilizando os [tex]80\, m[/tex] de tela que ele tem em casa.
Determinar as possíveis dimensões do terreno que será cercado, de modo que a área da horta não fique inferior a [tex]364\, m^2[/tex].


Lembretes
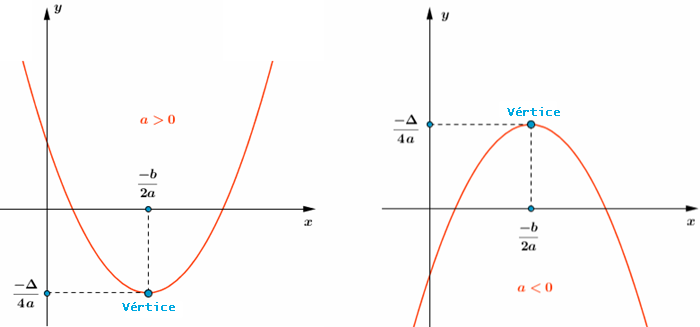
[tex]{\color{#800000}(1)}[/tex] O gráfico de uma função quadrática [tex]h:\mathbb{R}\rightarrow \mathbb{R}[/tex] dada por [tex]h(x)=ax^2+bx+c,\, a\not=0[/tex], é uma parábola com diretriz paralela ao eixo [tex]Oy[/tex], eixo de simetria paralelo ao eixo [tex]Oy[/tex], sendo sua concavidade voltada para cima se [tex]a\gt 0[/tex] e voltada para baixo se [tex]a\lt0[/tex].
[tex]{\color{#800000}(2)}[/tex] Se [tex]\Delta= b^2-4ac[/tex], as coordenadas do vértice da parábola são dadas por [tex](x_v,y_v)=\bigg(\dfrac{-b}{2a},\dfrac{-\Delta}{4a}\bigg)[/tex], sendo que [tex]x_v=\dfrac{-b}{2a}\, [/tex] e [tex]\, y_v=\dfrac{-\Delta}{4a}[/tex] indicam, respectivamente:
✓ o ponto de mínimo e o valor mínimo da função [tex]h[/tex], se a concavidade estiver voltada para cima;
✓ o ponto de máximo e o valor máximo da função [tex]h[/tex], se a concavidade estiver voltada para baixo.
Visualizem as informações fornecidas no lembrete [tex]{\color{#800000}(2)}[/tex], se [tex]\Delta \gt 0[/tex],
clicando no botão abaixo.
Solução
Vamos supor que [tex]x[/tex] e [tex] y[/tex] sejam os comprimentos dos lados do terreno que será cercado.

- Como o agricultor tem [tex]80\, m[/tex] de tela que poderão ser utilizados, então o perímetro desse terreno deve ser no máximo [tex]80\, m:[/tex]
- Como a área da horta não pode ser inferior a [tex]364\, m^2[/tex], então:
[tex]\qquad 2x+2y \leqslant 80\\
\qquad x+y \leqslant 40\\
\qquad y \leqslant 40-x.\qquad \textcolor{#800000}{(i)}[/tex]
[tex]\qquad xy \geqslant 364.\qquad \textcolor{#800000}{(ii)}[/tex]
Como [tex]x[/tex] é um comprimento, então [tex]x \gt 0[/tex]; logo, segue de [tex]\textcolor{#800000}{(i)}[/tex] que
[tex]\qquad xy \leqslant 40x-x^2,\qquad \textcolor{#800000}{(iii)}[/tex]
portanto, por [tex]\textcolor{#800000}{(ii)}[/tex] e [tex]\textcolor{#800000}{(iii)}[/tex], concluímos que:
[tex]\qquad 364 \leqslant xy \leqslant 40x-x^2[/tex]
[tex]\qquad 364 \leqslant 40x-x^2 [/tex]
[tex]\qquad x^2-40x+364 \leqslant 0. \qquad \textcolor{#800000}{(iv)}[/tex]
Observando o gráfico da função real definida pela expressão [tex]f(x)=x^2-40x+364 [/tex], a desigualdade [tex]\textcolor{#800000}{(iv)}[/tex] nos mostra que os valores de [tex]x[/tex] que satisfazem o problema são os números reais positivos para os quais a função [tex]f[/tex] é negativa ou nula ([tex]f(x) \leqslant 0 [/tex]); por isso vamos analisar o sinal de [tex]f[/tex] e, consequentemente, o sinal da expressão [tex]\boxed{x^2-40x+364}.[/tex]
Para traçar o gráfico de [tex]\, f[/tex] e analisar a variação de sinal, vamos precisar das raízes da equação de segundo grau [tex]x^2-40x+364=0.[/tex] São elas:
[tex]\qquad x=\dfrac{40\pm\sqrt{40^2-4\cdot 1\cdot 364}}{2} [/tex]
[tex]\qquad x=\dfrac{40\pm\sqrt{144}}{2} [/tex]
[tex]\qquad x=\dfrac{40\pm12}{2} [/tex]
[tex]\qquad x_1=\dfrac{40+12}{2}\, \, [/tex] e [tex]\, \, x_2=\dfrac{40-12}{2} [/tex]
[tex]\qquad x_1=26\, \, [/tex] e [tex]\, \, x_2=14.[/tex]
Na imagem a seguir, à esquerda, vemos parte do gráfico de [tex]f[/tex]. À direita, vemos a ampliação do intervalo que contém os valores de [tex]x[/tex] para os quais [tex]f(x)\leqslant 0.[/tex]
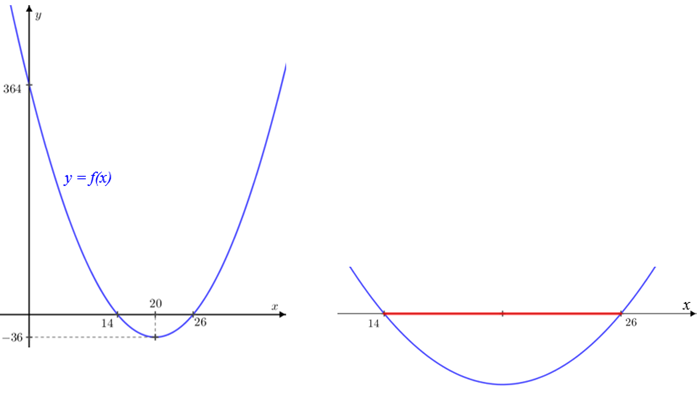
Dessa forma, os valores de [tex]x[/tex] que nos interessam estão no intervalo fechado [tex][14,26].[/tex]
E os valores de [tex]y[/tex]?
Observe que:
-
De [tex]14 \leqslant x \leqslant 26 [/tex], segue que [tex]14 \leqslant x [/tex] e [tex] x \leqslant 26[/tex]. Assim, temos as seguintes equivalências:
[tex]14 \leqslant x \iff -x \leqslant -14 \iff 40-x \leqslant 40-14 \iff 40-x \leqslant 26 .[/tex]
Assim, [tex]y \leqslant 40-x \leqslant 26[/tex], donde:
[tex]\qquad \qquad y \leqslant 26.\qquad \textcolor{#800000}{(v)}[/tex]
Como [tex]y \gt 0[/tex], de [tex] x \leqslant 26[/tex] segue que [tex] xy \leqslant 26y[/tex], Dessa forma, como [tex]xy \geqslant 364[/tex], temos que [tex] 364 \leqslant xy \leqslant 26y[/tex], donde [tex] 364 \leqslant 26y[/tex] e, portanto:
[tex] \qquad \qquad 14\leqslant y.\qquad \textcolor{#800000}{(vi)}[/tex]
De [tex]\textcolor{#800000}{(v)}[/tex] e [tex]\textcolor{#800000}{(vi)}[/tex], concluímos que [tex] 14\leqslant y \leqslant 26[/tex] e, com isso, os valores de [tex]y[/tex] que nos interessam também estão no intervalo fechado [tex][14,26].[/tex]
É importante observar que, embora [tex] 14\leqslant x,y \leqslant 26[/tex], não podemos, por exemplo, tomar [tex] x=14[/tex] e [tex] y=16[/tex]. Perceba que nesse caso temos [tex] x+y=14+16=30\leqslant 40 [/tex], mas [tex] xy=14\cdot 16=224 [/tex] e, portanto, a área da horta seria menor do que [tex]364[/tex].
Também não podemos fazer [tex] x=26[/tex] e [tex] y=22[/tex], por exemplo. Perceba que nesse caso temos [tex] xy=26\cdot 22=572 \geqslant 364[/tex], mas [tex] x+y=26+22=48\geqslant 40 [/tex] e o perímetro da horta seria maior do que os [tex]80\, m[/tex] de tela que o agricultor tem para cercá-la.
Concluindo, as possíveis dimensões [tex]x[/tex] e [tex]y[/tex] da horta são tais que:
[tex] \, \fcolorbox{black}{#eee0e5}{$14\leqslant x,y \leqslant 26 \text{, com } x+y \leqslant 40 \text{ e } \, xy \geqslant 26$}\, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução geométrica
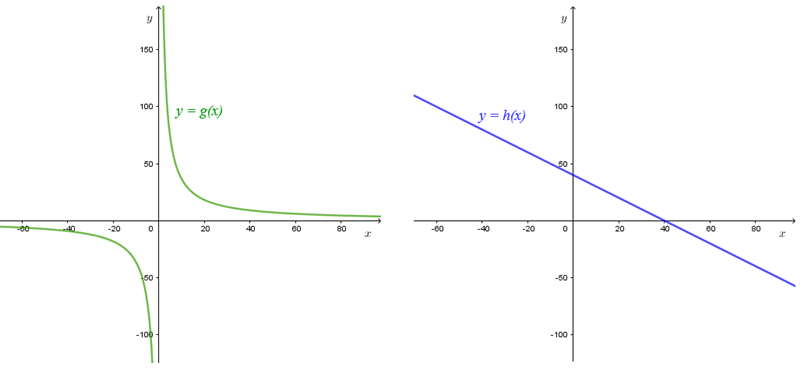
Se você conhece os gráficos das funções reais [tex]g[/tex] e [tex]h[/tex] assim definidas
[tex]\begin{array}{c c c}
g:\mathbb{R}^*\rightarrow \mathbb{R}&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&h:\mathbb{R}\rightarrow\mathbb{R}\\
g(x)=\dfrac{364}{x}&\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&h(x)=40-x
\end{array}[/tex]
podemos visualizar as infinitas soluções deste problema. Veja um esboço dos gráficos!
Para obter a solução graficamente, vamos observar as condições impostas no problema e para isso vamos considerar que [tex]x[/tex] e [tex] y[/tex] sejam os comprimentos dos lados do terreno que será cercado.
Então:
- Por serem comprimentos, [tex]\boxed{x \gt 0}[/tex] e [tex]\boxed{ y \gt 0}.[/tex]
- Como o agricultor dispõe de [tex]80\, m[/tex] de tela para fazer a cerca, então o perímetro do terreno deve ser no máximo [tex]80\, m[/tex] e assim [tex]2x+2y \leqslant 80[/tex], ou seja, [tex]\boxed{y \leqslant 40-x}.[/tex]
- Como a área da horta é no mínimo [tex]364\, m^2[/tex], então [tex]xy \geqslant 364[/tex], ou seja, [tex]\boxed{y \geqslant \dfrac{364}{x}}.[/tex]
Vamos inicialmente estudar isoladamente as duas condições principais que definem a solução do problema: [tex]\boxed{xy\geqslant 364}[/tex] e [tex]\boxed{ x+y \leqslant 40}[/tex], lembrando sempre que [tex]x \gt 0[/tex] e [tex] y \gt 0.[/tex]
- [tex]y \geqslant \dfrac{364}{x}[/tex], com [tex]x \gt 0[/tex] e [tex] y \gt 0[/tex]
- [tex]y \leqslant 40-x[/tex], com [tex]x \gt 0[/tex] e [tex] y \gt 0[/tex]
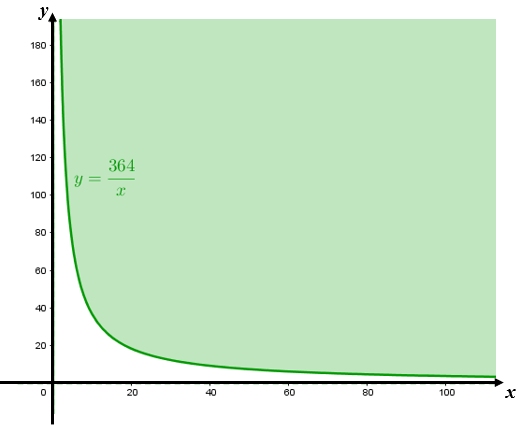
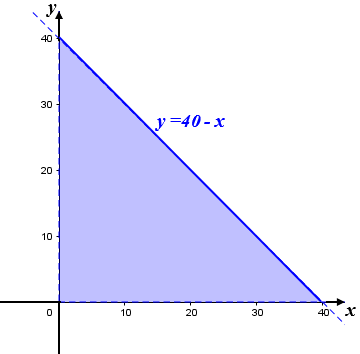
Fazendo a interseção das duas regiões mostradas acima, obtemos a solução gráfica do problema. Para ajudar na visualização da região de interseção, e consequente solução do problema, vamos determinar os pontos de interseção da curva [tex]y=\dfrac{364}{x}[/tex] e da reta [tex]y=40-x:[/tex]
[tex]\qquad \dfrac{364}{x}=40-x[/tex]
[tex]\qquad 364=40x-x^2[/tex]
[tex]\qquad x^2-40x+364=0[/tex]
[tex]\qquad x=\dfrac{40\pm\sqrt{40^2-4\cdot 1\cdot 364}}{2} [/tex]
[tex]\qquad x=\dfrac{40\pm\sqrt{144}}{2} [/tex]
[tex]\qquad x=\dfrac{40\pm12}{2} [/tex]
[tex]\qquad x_1=\dfrac{40+12}{2}\, \, [/tex] e [tex]\, \, x_2=\dfrac{40-12}{2} [/tex]
[tex]\qquad \boxed{x_1=26}\, \, [/tex] e [tex]\, \, \boxed{x_2=14}.[/tex]
Eis a representação gráfica da solução do problema, destacada em vermelho:
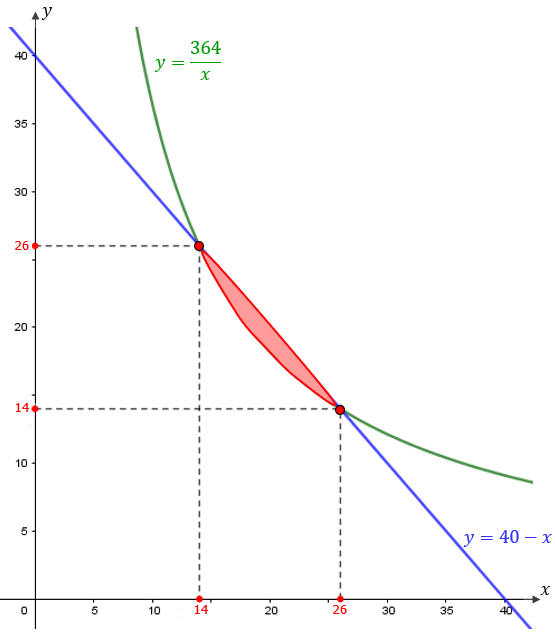
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
