Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
Seja [tex]P[/tex] um ponto do interior de um quadrado [tex]ABCD.[/tex]
Se as áreas dos triângulos [tex]APD[/tex] e [tex] BPC [/tex] são [tex]8\, \text{cm}^2\, [/tex] e [tex]\, 10\, \text{cm}^2[/tex], respectivamente, qual o comprimento em milímetros de cada diagonal do quadrado [tex]ABCD[/tex] ?

Lembretes
Vamos resolver este problema utilizando apenas resultados bem conhecidos da Geometria:
✐ Teorema de Pitágoras: Em um triângulo retângulo, o quadrado da hipotenusa é a soma dos quadrados dos catetos.
✐ Área do triângulo:[tex]\dfrac{\text{base $\times$ altura}}{2}[/tex]
Solução
Para ajudar na visualização da solução, vamos completar a figura do problema, mostrando os triângulos [tex]APD[/tex] e [tex] BPC [/tex] e duas de suas respectivas alturas, cujos comprimentos em centímetros denotaremos por [tex]h_1[/tex] e [tex]h_2.[/tex] O comprimento em centímetros dos lados do quadrado [tex]ABCD\, [/tex] será denotado por [tex]l.[/tex]
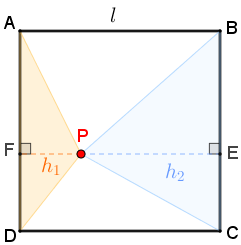
- Vamos observar as áreas dos triângulos [tex]APD[/tex] e [tex]BPC[/tex], denotando-as por [tex]S_{APD}[/tex] e [tex] S_{BPC}[/tex], respectivamente.
- Mas perceba que [tex]h_1+h_2=l[/tex]; assim, segue que:
- Agora, vamos observar o triângulo retângulo [tex]BCD[/tex]. Como seus catetos são os lados do quadrado, eles têm comprimento [tex]6\, \text{cm}[/tex] e sua hipotenusa é uma das diagonais do quadrado [tex]ABCD[/tex]. Logo, se denotarmos o comprimento em centímetros do segmento [tex]BD[/tex] por [tex]x[/tex], podemos utilizar o Teorema de Pitágoras e obter o comprimento em centímetros de cada diagonal do quadrado [tex]ABCD.[/tex]
|
Triângulo [tex]APD[/tex]: [tex]S_{APD}=\dfrac{\text{base $\times$ altura}}{2}[/tex] [tex]8=\dfrac{l \times h_1}{2}[/tex] [tex]h_1=\dfrac{16}{l}[/tex] |
Triângulo [tex]BPC[/tex]: [tex]S_{BPC}=\dfrac{\text{base $\times$ altura}}{2}[/tex] [tex]10=\dfrac{l \times h_2}{2}[/tex] [tex]h_2=\dfrac{20}{l}[/tex] |
[tex]h_1+h_2=l[/tex]
[tex]\dfrac{16}{l}+\dfrac{20}{l}=l[/tex]
[tex]l^2=16+20[/tex]
[tex]l=\pm \sqrt{16+20}[/tex]
[tex]l=\pm 6.[/tex]
Como [tex]l[/tex] é um comprimento, concluímos que [tex]\fcolorbox{black}{#d7d7d7}{$l=6\, \text{cm}$}.[/tex]
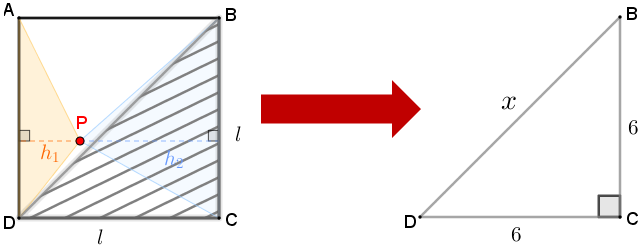
Vamos aos cálculos:
[tex]\qquad 6^2+6^2=x^2[/tex]
[tex]\qquad 36+36=x^2[/tex]
[tex]\qquad 2 \times 36=x^2[/tex]
[tex]\qquad x=\pm \sqrt{ 2 \times 36}[/tex]
[tex]\qquad x=\pm 6 \sqrt{2}.[/tex]
Como [tex]x[/tex] é um comprimento, [tex]x=6 \sqrt{2}[/tex] e, portanto, temos que a diagonal do quadrado [tex]ABCD[/tex] mede [tex]\fcolorbox{black}{#d7d7d7}{$6 \sqrt{2}\, \text{cm}$}.[/tex]
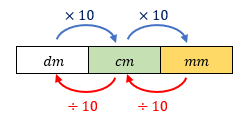
- Para finalizarmos a solução do problema, precisamos converter [tex]6 \sqrt{2}\, \text{cm}\, [/tex] em [tex]\, \text{mm}.[/tex]
- Comprimento da diagonal do quadrado [tex]ABCD[/tex] em [tex]mm:[/tex]
[tex]\qquad 6 \sqrt{2} \times 10 \longmapsto\fcolorbox{black}{#eee0e5}{$60 \sqrt{2}\, \text{mm} \approx 84,85\, \text{mm}$}.[/tex]
E, para isso, o esqueminha abaixo pode ajudar!
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
