Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Fácil )
No jardim circular de uma pracinha foram feitos três canteiros, conforme vista superior do jardim mostrada na figura a seguir.
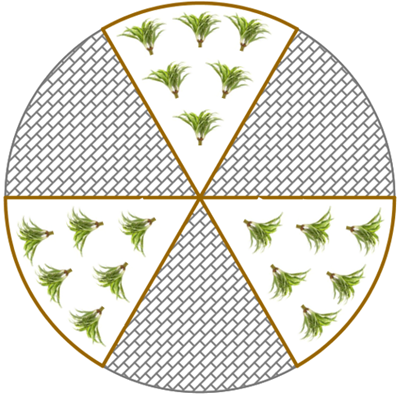
O círculo tem [tex]4 \, m[/tex] de raio e os canteiros e as calçadas foram construídos a partir de ângulos centrais com a mesma medida.
Para proteção das plantinhas, que ainda estão crescendo, serão colocadas cercas nas linhas marrons que contornam os canteiros, conforme mostra a figura.
Quantos metros de cerca serão necessários?
Para efeito de cálculos, utilize [tex] \, \pi=3,14 \, [/tex] e expresse o resultado em um número inteiro de metros.

Ajuda
✐ A um arco de circunferência podemos associar duas medidas distintas:
– a sua medida angular;
– a sua medida linear.
Ambas podem ser obtidas a partir da medida angular e do comprimento da circunferência que define o arco; mas, se você não se lembra delas, clique AQUI. (Não se esqueça de fechar a janelinha que se abriu com as informações, depois de utilizá-la.)
Solução
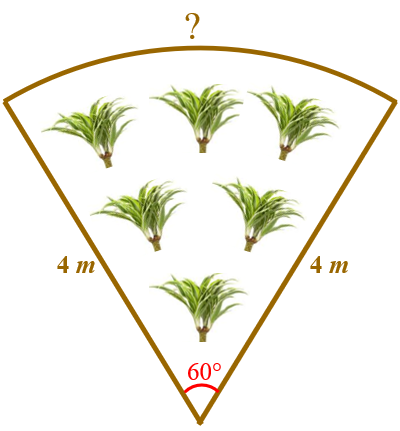
As figuras que representam os três canteiros e as três calçadas são o que chamamos na Matemática de setores circulares. Mais precisamente, setores circulares menores. (Se necessário, clique AQUI para aprender um pouco mais sobre setor circular.) Como os seis setores foram construídos a partir de ângulos centrais com a mesma medida, os ângulos que os definem medem [tex]\dfrac{360^\circ}{6}=60^\circ[/tex] cada. Precisamos, então, calcular o perímetro de um setor circular definido por um ângulo de [tex]60^\circ[/tex].
Perceba que o perímetro de cada setor circular é a soma de duas medidas do raio da circunferência e do comprimento de um arco dessa mesma circunferência correspondente a [tex]60^\circ[/tex], conforme ilustra a figura ao lado.
Como a medida do raio é [tex]4 \, m[/tex], para resolver este problema, precisaremos calcular o comprimento de arco, ou seja, a medida linear do arco em questão. Pra isso, utilizaremos a Ajuda e uma regra de três simples:
[tex] \begin{array}{c c c}
\text{comprimento da circunferência} &\text{————–}&360^\circ\\
\text{comprimento do arco} &\text{————–}& 60^\circ
\end{array}[/tex].
Para os cálculos, precisaremos do comprimento [tex]c[/tex] de uma circunferência de raio [tex]4 \, m[/tex]:
[tex]\qquad c=2\times \pi \times r[/tex]
[tex]\qquad c=2\times 3,14 \times 4[/tex]
[tex]\qquad c=25,12 \, m \, .[/tex]
Agora, se denotarmos o comprimento em metros do arco de circunferência em questão por [tex]l[/tex], podemos reescrever a nossa regra da três da seguinte forma:
[tex] \begin{array}{c c c}
25,12 \, m \, &\text{————–}&360^\circ\\
l &\text{————–}& 60^\circ
\end{array}[/tex]
obtendo que:
[tex]\quad 25,12 \, m \times 60^\circ=l \times 360^\circ[/tex]
[tex]\quad l=\dfrac{25,12 \, m \times 60^\circ}{360^\circ}[/tex]
[tex]\quad \boxed{l=\dfrac{25,12}{6}m} \, .[/tex]
Com isso, o perímetro de cada setor circular, que é a quantidade [tex]Q[/tex] de cerca a ser comprada para cada canteiro, é dado por:
[tex]\qquad \boxed{Q=8+\dfrac{25,12}{6}} \, .[/tex]
Como são três canteiros, serão necessários
[tex]\qquad 3 \times \left(8+\dfrac{25,12}{6}\right)=24+12,56=\boxed{36,56}[/tex] metros de tela.
Para finalizar, observe que [tex]36 \lt \boxed{36,56} \lt 37[/tex]; portanto, serão necessários [tex] \, \fcolorbox{black}{#eee0e5}{$37 \text{ metros }$}[/tex] de cerca para isolar os três canteiros e proteger as plantinhas.
O comprimento em metros [tex]l[/tex] do arco da circunferência relativo a cada canteiro poderia ser obtido observando-se que, como os ângulos centrais que definem os canteiros têm a mesma medida, então cada um dos seis arcos corresponde a [tex]\frac{1}{6}[/tex] do comprimento total da circunferência.
Assim:
[tex]\qquad l=\dfrac{2 \pi r}{6}= \dfrac{2 \times 3,14 \times 4}{6}=\dfrac{25,12}{6} \, m.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
