Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 8º ano do E. F. – Nível de dificuldade: Médio)
Em uma urna, foram colocadas bolinhas numeradas de [tex]1[/tex] a [tex]6[/tex], uma de cada número.
Serão sorteadas três dessas bolinhas de modo que uma bolinha sorteada não volte para a urna.
Supondo que as seis bolinhas têm a mesma chance de serem sorteadas, em quantas possibilidades os números formados pela primeira, pela segunda e pela terceira bolinhas sorteadas, nessa ordem, começam pelo algarismo [tex]4[/tex]?

Ajuda
Princípio Fundamental da Contagem, ou Princípio Multiplicativo, para três decisões :
Se uma decisão A puder ser tomada de [tex] m [/tex] maneiras, uma decisão B puder ser tomada de [tex]n [/tex] maneiras, uma decisão C puder ser tomada de [tex]p [/tex] maneiras, e a tomada de uma decisão não mude a quantidade de possibilidades para a tomada de outra, então a quantidade de maneiras de se tomar essas três decisões ao mesmo tempo é dada pelo produto: [tex]\boxed{m\times n \times p} \, .[/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
Solução
Observe que:
- Vamos formar um número com três algarismos, cujo algarismo das centenas é [tex]4[/tex].
- Esse número terá os algarismos distintos, já que cada bolinha sorteada não volta para a urna.
- São seis os números disponíveis para o sorteio.
Assim, pelo Princípio Multiplicativo, o número pode ser formado de [tex] \, \fcolorbox{black}{#eee0e5}{$1\times 5 \times 4=20$}[/tex] modos.
Observe as possibilidades:
[tex]\begin{array}{c c c}
\underline{\text{ 1 possibilidade}}&\underline{\text{ 5 possibilidades }}&\underline{\text{ 4 possibilidades }}\\
\substack{\text{algarismo das}\\ \text{centenas}}&\substack{\text{algarismo das}\\ \text{dezenas}}&\substack{\text{algarismo das}\\ \text{unidades}}
\end{array}[/tex].
Como a quantidade de algarismos é pequena, podemos desenhar a árvore de possibilidades para a formação dos números que atendem às exigências do enunciado:
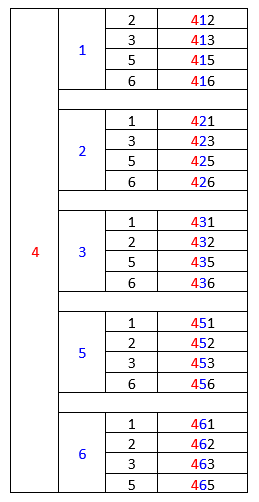
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
