Problema – Área do triângulo PQR
(FCMSCSP, 2021 – Adaptado) Um círculo de centro [tex]K[/tex] tangencia o lado [tex]\overline{RP}[/tex] de um triângulo retângulo [tex]PQR[/tex] de hipotenusa [tex]\overline{QR}[/tex]. Esse círculo gira, mantendo-se tangente a [tex]\overline{RP}[/tex], até tangenciar [tex]\overline{PQ}[/tex]. Em seguida, ele gira tangenciando [tex]\overline{PQ}[/tex], até tangenciar [tex]\overline{QR}[/tex]. Por fim, ele gira tangenciando [tex]\overline{QR}[/tex] até que seu centro [tex]K[/tex] volte à posição inicial.
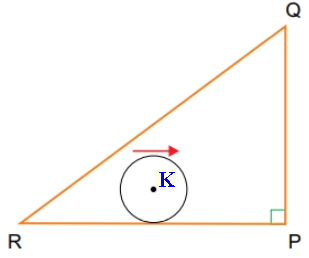
Sabendo-se que o raio do círculo mede [tex]1\;cm[/tex] e que os lados do triângulo medem [tex]RP = 8 \;cm[/tex], [tex]PQ = 6 \; cm[/tex] e [tex]QR = 10 \;cm[/tex], determine a área do triângulo formado pela trajetória descrita por [tex]K[/tex].
 |
Use o applet abaixo para ajudar na visualização do enunciado
|
Use um applet ajudar
Você pode utilizar este applet para ver o movimento do círculo e, principalmente, observar o triângulo descrito pela trajetória do centro [tex]K[/tex].
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para fazer o círculo girar, clique com o botão direito do mouse sobre o ponto K e selecione a opção Animação na janelinha que se abriu.
(3) Clique no ícone || que apareceu no canto inferior esquerdo da janela, para parar a animação.
(4) Clique no ícone ► que apareceu no canto inferior esquerdo da janela, para reiniciar a animação.
(5) Se quiser voltar para a visualização inicial, clique nas setinhas circulares que aparecem no canto superior direito do aplicativo.
OBMEP_ srdg, criado com o GeoGebra
 |
Para ver uma solução para este problema, clique aqui .
|
Equipe COM – OBMEP
