✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 9º ano do E. F.)
(FCMSCSP, 2021 – Adaptado) Um círculo de centro [tex]K[/tex] tangencia o lado [tex]\overline{RP}[/tex] de um triângulo retângulo [tex]PQR[/tex] de hipotenusa [tex]\overline{QR}[/tex]. Esse círculo gira, mantendo-se tangente a [tex]\overline{RP}[/tex], até tangenciar [tex]\overline{PQ}[/tex]. Em seguida, ele gira tangenciando [tex]\overline{PQ}[/tex], até tangenciar [tex]\overline{QR}[/tex]. Por fim, ele gira tangenciando [tex]\overline{QR}[/tex] até que seu centro [tex]K[/tex] volte à posição inicial.
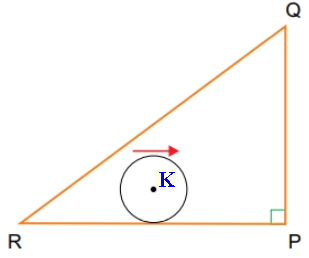
Sabendo-se que o raio do círculo mede [tex]1\;cm[/tex] e que os lados do triângulo medem [tex]RP = 8 \;cm[/tex], [tex]PQ = 6 \; cm[/tex] e [tex]QR = 10 \;cm[/tex], determine a área do triângulo formado pela trajetória descrita por [tex]K[/tex].
Um applet para ajudar na visualização do enunciado
Você pode utilizar este applet para ver o movimento do círculo e, principalmente, observar o triângulo descrito pela trajetória do centro [tex]K[/tex].
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para fazer o círculo girar, clique com o botão direito do mouse sobre o ponto K e selecione a opção Animação na janelinha que se abriu.
(3) Clique no ícone || que apareceu no canto inferior esquerdo da janela, para parar a animação.
(4) Clique no ícone ► que apareceu no canto inferior esquerdo da janela, para reiniciar a animação.
(5) Se quiser voltar para a visualização inicial, clique nas setinhas circulares que aparecem no canto superior direito do aplicativo.
OBMEP_ srdg, criado com o GeoGebra

Lembrete para a Solução 1
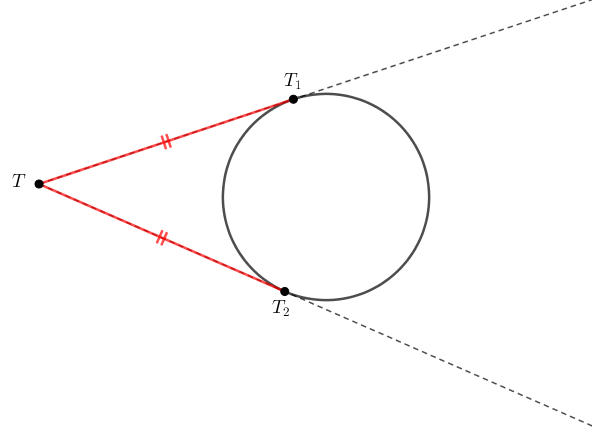
Relação dos segmentos tangentes: Se de um ponto [tex]T[/tex] conduzirmos os segmentos [tex]\overline{TT_1}[/tex] e [tex]\overline{TT_2}[/tex] tangentes a uma circunferência, sendo [tex]T_1[/tex] e [tex]T_2[/tex] pontos da circunferência, então [tex]\overline{TT_1}[/tex] e [tex]\overline{TT_2}[/tex] têm o mesmo comprimento.
Solução 1
Como o raio do círculo mede [tex]1 \;cm[/tex], então a distância entre os lados do triângulo [tex]PQR[/tex] e os lados correspondentes do triângulo formado pela trajetória do círculo é igual a [tex]1 \;cm[/tex], ou seja, os lados são paralelos, o que implica que os ângulos internos correspondentes dos triângulos têm as mesmas medidas e, portanto, os triângulos são semelhantes.
Por outro lado, utilizando o Lembrete, podemos concluir que os segmentos tangentes aos círculos partindo do vértice [tex]R~[/tex], e também do vértice [tex]~Q[/tex], até os respectivos pontos de tangência têm o mesmo comprimento: digamos [tex]x~[/tex] e [tex]~y.[/tex]
Observe a figura abaixo.
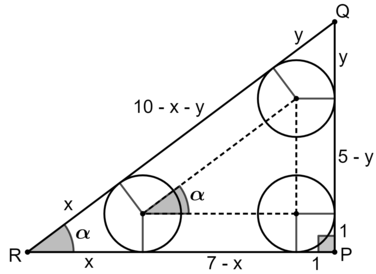
Agora, sendo [tex]\alpha[/tex] a medida do ângulo [tex]P\hat{R}Q[/tex], temos [tex]\text{sen} \;\alpha = \dfrac{6}{10}[/tex] e [tex]\cos \;\alpha = \dfrac{8}{10}[/tex]. Assim, em relação ao triângulo menor, devemos ter:
[tex]\quad \begin{cases}\text{sen} \;\alpha = \dfrac{5-y}{10-x-y} = \dfrac{6}{10}\\
\cos \;\alpha = \dfrac{7-x}{10-x-y} = \dfrac{8}{10}
\end{cases}.[/tex]
Com isso, segue que:
[tex]\quad \begin{cases}10\cdot (5-y)= 6\cdot (10-x-y)\\
10\cdot (7-x) = 8\cdot (10-x-y)
\end{cases}[/tex]
ou ainda:
[tex]\quad \begin{cases}6x-4y= 10\\
2x-8y = -10
\end{cases}.[/tex]
Multiplicando a segunda equação do último sistema por [tex]-3[/tex] e somando à primeira, obtemos [tex]20y = 40[/tex] e assim [tex]y = 2 \;cm.[/tex]
Substituindo o valor de [tex]y[/tex] na primeira equação do último sistema, obtemos [tex]x = 3 \;cm[/tex].
Logo, a área [tex]A[/tex] do triângulo formado pela trajetória descrita por [tex]K[/tex] é
[tex]\quad A=\dfrac{(7-x)(5-y)}{2} = \dfrac{4\cdot 3}{2}\\
\quad \boxed{A= 6 \;cm^2}.[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Sabemos que o raio do círculo que gira mede [tex]1 \text{ cm}[/tex]; assim, as distâncias entre os lados do triângulo [tex]RPQ[/tex] e os lados correspondentes do triângulo [tex]ABC[/tex] definido pela trajetória do círculo são iguais a [tex]1 \text{ cm}[/tex].
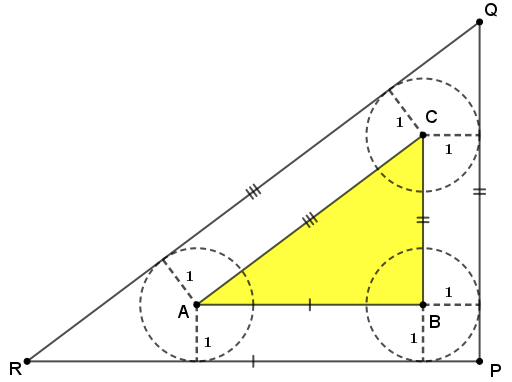
Dessa forma, os lados correspondentes dos dois triângulos são paralelos, o que implica nos ângulos internos correspondentes dos triângulos terem a mesma medida e, consequentemente, os triângulos [tex]RPQ[/tex] e [tex]ABC[/tex] são semelhantes.
Podemos, então, concluir que os lados do triângulo [tex]ABC[/tex] medem [tex]6k\text{ cm}[/tex], [tex]8k\text{ cm}[/tex] e [tex]10k\text{ cm}[/tex], sendo [tex]k \gt 0[/tex] a constante de proporcionalidade. Observe a figura.
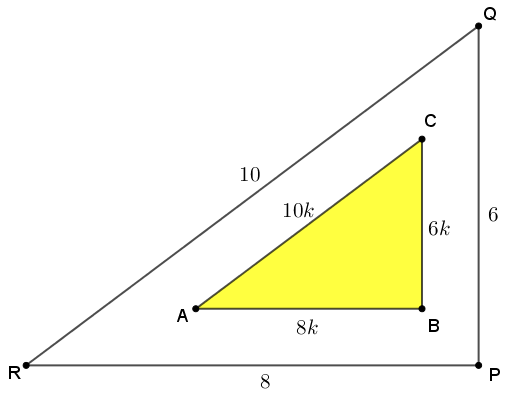
Perceba que podemos decompor a área interna do triângulo [tex]RPQ[/tex] como a área do triângulo [tex]ABC[/tex] e dos trapézios [tex]ARPB[/tex], [tex]BPQC[/tex] e [tex]CQRA[/tex]; portanto temos a seguinte soma de áreas:
[tex]\qquad S_{RPQ}=S_{ABC}+S_{ARPB}+S_{BPQC}+S_{CQRA}\,.[/tex]
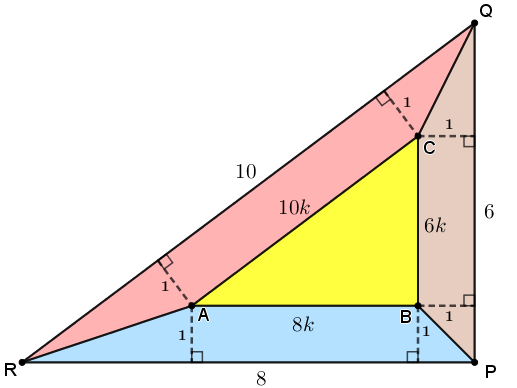
Vamos aos cálculos:
[tex]\qquad S_{RPQ}=S_{ABC}+S_{ARPB}+S_{BPQC}+S_{CQRA}\\
\qquad \dfrac{8 \times 6}{2}=\dfrac{8k \times 6k}{2}+\dfrac{\left(8+8k \right)\times1}{2}+\dfrac{\left(6+6k \right)\times1}{2}+\dfrac{\left(10+10k \right)\times1}{2}\\
\qquad \dfrac{8 \times 6}{2}=\dfrac{8k \times 6k}{2}+\dfrac{8+8k}{2}+\dfrac{6+6k}{2}+\dfrac{10+10k}{2}\\
\qquad \dfrac{8 \times 6}{\cancel{2}}=\dfrac{8k \times 6k}{\cancel{2}}+\dfrac{8+8k}{\cancel{2}}+\dfrac{6+6k}{\cancel{2}}+\dfrac{10+10k}{\cancel{2}}\\
\qquad 48=48k^2+24+24k\\
\qquad 2=2k^2+1+k\\
\qquad 2k^2+k-1=0.[/tex]
Agora, vamos determinar os valores de [tex]k[/tex] que satisfazem a equação [tex]\boxed{2k^2+k-1=0}[/tex]:
[tex]\qquad k =\dfrac{-1\pm\sqrt{1+8~}}{2\times 2}\\
\qquad k =\dfrac{-1\pm 3}{4}\\
\qquad k =\dfrac{-1+ 3}{4} \text{ ou } k =\dfrac{-1- 3}{4}\\
\qquad k =\dfrac{1}{2} \text{ ou } k =-1.\\
[/tex]
Finalmente, observe que [tex]6k[/tex], [tex]8k[/tex] e [tex]10k[/tex] são comprimentos, o que nos leva a eliminar o valor [tex]k =-1[/tex]. Assim, os lados do triângulo [tex]ABC[/tex] são [tex]6\times \dfrac{1}{2}[/tex], [tex]8\times \dfrac{1}{2}[/tex] e [tex]10\times \dfrac{1}{2}[/tex], ou seja, [tex]3[/tex], [tex]4[/tex] e [tex]5[/tex] centímetros.
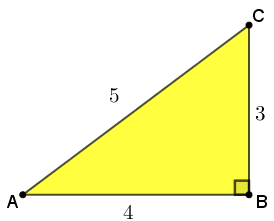
Com isso, concluímos que
[tex]\qquad S_{ABC}= \dfrac{4 \times 3}{2}=\boxed{6 { cm}^2}\,.[/tex]
Solução elaborada pelos Moderadores do Blog.
