Clique no botão abaixo para visualizar a Sala.
2) Agora, Júlia quer dividir um número diferente de balas entre 13 amigos, de modo que cada um deles receba 4 balas a mais do que restará a ela. Quais as quantidades possíveis de balas que Júlia pode ter?
Muitas questões em nosso cotidiano, como as apresentadas acima, envolvem restos; e o ramo da Matemática responsável pelo seu estudo é a Aritmética dos Restos ou Aritmética Modular. Apesar de questões como estas serem resolvidas comumente pelo “Algoritmo da Divisão Euclidiana”, alguns problemas e demonstrações mais complexas exigem um conhecimento aprofundado do assunto, bem como notações mais elaboradas.
Há muito estudo sobre o tema em livros sobre Aritmética e Teoria dos Números. No entanto, apesar de utilizarmos os restos de divisões para resolver inúmeros problemas, tanto teóricos quanto reais, esse assunto não está presente nos currículos do Ensino Médio e, portanto, o material destinado aos alunos nessa fase de ensino é escasso.
O objetivo desta Sala de Estudos é permitir que você, caro leitor, aprofunde um pouco mais seus conhecimentos acerca dos elementos da divisão e, sobretudo, do resto. Ao final do conteúdo, apresentaremos também alguns problemas sobre o assunto, muito comuns tanto em concursos e vestibulares como em Olimpíadas de Matemática mais avançadas.
Se você ficou curioso(a) com relação às soluções dos problemas apresentados acima, é só clicar no botão abaixo!
2) Pelo Algoritmo da Divisão Euclidiana, o qual veremos logo adiante, temos que o problema pode ser equacionado do seguinte modo: sendo [tex]a[/tex] a quantidade inicial de balas, então:
[tex]\quad a=13(r+4)+r[/tex], sendo [tex]0\leq r \leq12, r \in \mathbb{ℤ}. [/tex]
Os valores positivos de [tex]a[/tex] que podem ser obtidos a partir dessas informações são, portanto, os seguintes:
[tex]\qquad a \in \{52,66,80,94,108,122,136,150,164,178,192,206,220\}.[/tex]
I – Divisão e Aritmética: Um pouco de História…
De acordo com os historiadores, quem introduziu o estudo da Matemática na Grécia, berço do pensamento ocidental, foi Tales de Mileto (640-546 a.C.). Tales teria trazido consigo para a Grécia os conhecimentos de Geometria e Aritmética que aprendera com os sacerdotes egípcios. Interessado em Astronomia e Filosofia, Tales difundiu a Geometria na sua cidade, chamada Mileto. Ao fazê-lo, acabou por introduzir uma inovação revolucionária que em muito se diferia da matemática egípcia: a ideia de que as verdades matemáticas devem ser provadas. A diferença entre a Matemática que se iniciava na Grécia Antiga e a egípcia era que, enquanto para os egípcios ela se tratava de uma arte que os auxiliava em seus trabalhos de engenharia e agrimensura, na Grécia ela adquiriu de fato um caráter científico, graças à atividade filosófica que lá já se desenvolvia. (Para saber mais sobre Tales de Mileto, clique AQUI.)
Logo em seguida, foi Pitágoras de Samos (580-500 a.C.), discípulo de Tales, quem, juntamente com sua famosa e histórica Escola Pitagórica, se encarregou de desenvolver e difundir a Matemática pela Grécia e suas colônias. A Escola Pitagórica atribuía aos números um poder místico, havendo uma ideia de que o Universo era regido por uma inteligência superior, essencialmente matemática. (Para saber mais sobre Pitágoras, clique agora AQUI.)
Os gregos tinham uma forte inclinação à filosofia e à lógica, de modo que isto influenciou fortemente toda a sua cultura e, particularmente, seu modo de fazer Matemática. Um grande exemplo disso foi o filósofo Platão (429-348 a.C.) que, apesar de não ser matemático, nela via um treinamento indispensável ao filósofo, pois ressaltava a metodologia axiomático-dedutiva a ser seguida, de acordo com ele, em todos os campos do conhecimento. A importância que Platão atribuía à Matemática era tão forte que o fez escrever no portal de sua escola a famosa frase “Que não entre nesse local alguém ignorante em Geometria”.
Com toda essa herança cultural, surge em Alexandria, por volta de 300 a.C., um tratado que futuramente viria a se tornar um dois mais importantes da Matemática, Os Elementos, de Euclides. Esse tratado, composto por treze livros, contém a maior parte do conhecimento matemático da época sistematizado.
Dos treze livros de Os Elementos, dez tratam de Geometria e três, de Álgebra. Em um desses três, o livro VII, Euclides define os conceitos de divisibilidade, de número primo, de números perfeitos, de máximo divisor comum (MDC) e mínimo múltiplo comum (MMC), entre outros. Nesse livro, além das definições feitas, todas bem definidas e até hoje muito utilizadas, encontra-se enunciada a divisão com resto de um número natural por outro, chamada divisão euclidiana. Com o uso dessa divisão, Euclides estabelece o algoritmo mais eficiente para se fazer o cálculo do MDC entre dois inteiros, chamado de Algoritmo de Euclides. (Para saber mais sobre Euclides, clique AQUI.)
Após Euclides, a Aritmética estagnou-se por cerca de 500 anos, tendo ressuscitado com os trabalhos de Diofanto de Alexandria. A obra que ele nos legou chama-se Arithmetica e foi escrita também em treze volumes, apesar de nem todos terem chegado até nós, de modo a tornar-se o primeiro trabalho de Álgebra com abordagem não revestida de qualquer linguagem ou interpretação tão somente geométrica, como fizeram seus predecessores. Tido por muitos como “pai da álgebra”, uma das importantes contribuições de Diofanto são as chamadas equações diofantinas, as quais serão melhor exploradas nos tópicos seguintes. (Para saber mais sobre Diofanto, clique AQUI.)
II – A Divisão Euclidiana
A Divisão Euclidiana, ou divisão com resto, é uma operação que toda criança aprende na escola. Escrita de maneira formal, e não como ela é tratada nas séries iniciais do Ensino Fundamental, a Divisão Euclidiana afirma o seguinte:
[tex]\qquad x=y \cdot q+r[/tex], com [tex] 0 \leq r \lt y.[/tex]
Veja o esqueminha:
[tex]\qquad \qquad ~~~~~~~~~~~~~~~~~~~~ \begin{array}{r}
x \, \end{array} \begin{array}{|r}
\, y \, \, \, \\ \hline
\end{array}[/tex]
[tex]\qquad \qquad ~~~~~~~~~~~~~~~~~~~~ \begin{array}{r}
r
\end{array}\begin{array}{r}
\, \, \, q
\end{array}\qquad \qquad[/tex]
Para os nossos propósitos, precisaremos estender esse resultado para o conjunto dos números inteiros e, portanto, trabalharemos com o seguinte enunciado para a Divisão de Euclides:
As duas versões podem ser demonstradas pelo chamado Princípio da Boa Ordem ou Princípio da Boa Ordenação, o qual garante que: “Todo subconjunto não vazio do conjunto dos números naturais possui um menor elemento”.
Um caso particular, e geralmente o mais explorado ao iniciarmos o aprendizado sobre o processo de divisão quando crianças, é o caso em que a divisão é dita exata. Neste caso, o resto da divisão é igual a zero e podemos falar sobre o conceito de divisibilidade.
Definição: Dados números inteiros [tex]a~[/tex] e [tex]~b[/tex], com [tex]b \ne 0[/tex], dizemos que [tex]b[/tex] divide [tex]a[/tex], ou que [tex]b[/tex] é divisor de [tex]a[/tex], ou ainda que [tex]a[/tex] é múltiplo de [tex]b[/tex], quando existe um valor inteiro [tex]q[/tex] tal que [tex]a=b \cdot q[/tex], e neste caso denotamos [tex]b \mid a[/tex].
Quando não existe um inteiro [tex]q[/tex] satisfazendo [tex]a=b \cdot q[/tex], dizemos que [tex]b[/tex] não divide [tex]a[/tex] e denotamos [tex]b \nmid a[/tex].
Observe que neste último caso, vale a divisão euclidiana entre [tex]a~[/tex] e [tex]~b[/tex] com resto [tex]\textcolor{red}{1} \leq r \lt |b|.[/tex]
Observação: É comum não escrever o sinal [tex] \cdot[/tex] para indicarmos, por exemplo, o produto [tex]\boxed{g \cdot h}[/tex] e escrever esse produto apenas por justaposição dos fatores: [tex]\boxed{gh}.[/tex]
Não vamos aprofundar o estudo de divisibilidade, já temos muito material sobre esse assunto no nosso Blog. Mas vamos apresentar um resultado que será muito utilizado, implícita ou explicitamente, nas nossas discussões:
Propriedade (*): Sejam [tex]a~[/tex], [tex]b~[/tex] e [tex]~c[/tex] números inteiros, com [tex]c \ne 0.[/tex]
Se [tex]c \mid a~[/tex] e [tex]~c \mid b[/tex], então [tex]c \mid (ax+by)[/tex], para quaisquer [tex]x,y \in \mathbb{Z}.[/tex]
De [tex]c \mid a[/tex], segue que existe um inteiro [tex]m[/tex] tal que [tex]a=c m.[/tex]
De [tex]c \mid b[/tex], segue que existe um inteiro [tex]n[/tex] tal que [tex]b=c n.[/tex]
Assim, se [tex]x~[/tex] e [tex]~y[/tex] são números inteiros quaisquer, segue que:
[tex]\qquad ax+by=(cm)x+(cn)y=c(mx+ny).[/tex]
Então, se [tex]mx+ny=t[/tex], podemos afirmar que
[tex]\qquad \boxed{ax+by=ct \text{ com } t \in \mathbb{Z}}[/tex],
uma vez que [tex] m,n,x,y \in \mathbb{Z}.[/tex]
Assim, pela definição de divisibilidade no conjunto dos números inteiros, segue que [tex]c \mid (ax+by).[/tex]
O estudo da divisibilidade de inteiros é muito importante para o estudo de congruências, que trataremos logo a seguir, pois nos permite perceber se um número terá ou não resto zero em uma determinada divisão.
Vale lembrar que em algumas situações não precisamos fazer divisões para saber se um dado número [tex]a[/tex] é divisível por um dado número [tex]b[/tex]: basta utilizar os conhecidos como Critérios de Divisibilidade, que são regras que permitem verificar se um número é divisível por outro sem a realização de longos cálculos. Para conhecer alguns critérios de divisibilidade, clique AQUI.
III – Congruências
É bastante natural escrevermos 23+7=30. Porém, você já se deparou com uma igualdade do tipo “23+7=6”?
Em que contexto afirmar isso faz sentido?
Bem, nesta Sala de Estudos veremos que expressões como “23+7=6” fazem sentido quando estamos trabalhando com Congruências e Aritmética Modular. Ficou confuso(a)?
Então, imagine que Joana adormeceu às 23h e dormiu por 7 horas. Em que horário ela acordou?
Provavelmente, a sua primeira ideia de resolução foi somar 23+7. No entanto, não faz sentido dizer que Joana acordou às 30h do mesmo dia, afinal, o dia só tem 24 horas! Nesse contexto, estabelecer a igualdade “23+7=6” faz sentido, de modo que podemos dizer corretamente que Joana acordou às 6h do dia seguinte. Para diferenciar a igualdade “23+7=6” da igualdade usual 23+7=30, é usual escrever [tex]23+7\equiv6\, (\text{mod}\,24)[/tex], que podemos ler como “vinte e três mais sete é congruente a 6 módulo 24”.
Agora, vejamos uma definição formal da ideia apresentada acima:
Diz-se que [tex]a~[/tex] é congruente a [tex]~b[/tex] módulo [tex]m[/tex] (ou que [tex]a~[/tex] e [tex]~b[/tex] são congruentes) se, e somente se, [tex]m[/tex] divide a diferença [tex]a-b.[/tex]
Neste caso, escrevemos [tex]a\equiv b \,(\text{mod}\,m)[/tex] e lemos [tex]a~[/tex] é congruente a [tex]~b.[/tex]
Quando a relação [tex]a\equiv b \,(\text{mod}\,m)[/tex] é falsa, dizemos que [tex]a~[/tex] e [tex]~b[/tex] não são congruentes e denotamos este fato por [tex]a \not\equiv b \,(\text{mod}\,m).[/tex]
Por exemplo, temos que [tex]12\equiv 2 \,(\text{mod}\,5)[/tex], pois [tex]5\mid (12−2)~[/tex]; e [tex]~19\equiv 4 \,(\text{mod}\,15)[/tex], pois [tex]15\mid (19−4).[/tex] Mas [tex]11\not \equiv 4 \,(\text{mod}\,5)[/tex], já que [tex]5\nmid (11−4)[/tex]; e [tex]~25\not \equiv 6 \,(\text{mod}\,15)[/tex], já que [tex]15\nmid (25−6).[/tex]
Particularmente, [tex](23+7)\equiv6\, (\text{mod}\,24)[/tex], pois [tex]24\mid (30−6).[/tex]
Uma propriedade que será fundamental na utilização de congruências para conseguirmos definir a chamada Aritmética dos Restos irá relacionar congruências com restos de divisões euclidianas. Observe:
Então, [tex]a~[/tex] é congruente a [tex]~b[/tex] módulo [tex]m[/tex] se, e somente se, [tex]a~[/tex] e [tex]~b[/tex] deixam o mesmo resto quando divididos por [tex]m.[/tex]
Temos que provar duas afirmações:
(i) Se [tex]a~[/tex] é congruente a [tex]~b[/tex] módulo [tex]m[/tex], então [tex]a~[/tex] e [tex]~b[/tex] deixam o mesmo resto quando divididos por [tex]m.[/tex]
(ii) Se [tex]a~[/tex] e [tex]~b[/tex] deixam o mesmo resto quando divididos por [tex]m[/tex], então [tex]a~[/tex] é congruente a [tex]~b[/tex] módulo [tex]m.[/tex]
Vamos lá!
(i) Suponhamos que [tex]a~[/tex] é congruente a [tex]~b[/tex] módulo [tex]m.[/tex] Então, por definição, temos que [tex]m[/tex] divide a diferença [tex]a-b.[/tex]
Assim, existe [tex]k \in \mathbb{Z} [/tex] tal que [tex]\boxed{a-b=km}.[/tex]
Agora, seja [tex]r[/tex] o resto da divisão de [tex]b[/tex] por [tex]m[/tex]; então, pela Divisão Euclidiana, [tex]\boxed{b=qm+r}[/tex], sendo [tex]0 \leq r \lt m.[/tex]
Pelo exposto. segue que:
[tex]\qquad a=b+km=(qm+r)+km=(q+k)m+r.[/tex]
Como [tex]0 \leq r \lt m[/tex], pela unicidade do resto e do quociente de uma divisão, concluímos que
[tex]\quad \rhd q+k[/tex] é o quociente da divisão de [tex]a[/tex] por [tex]m.[/tex]
[tex]\quad \rhd r[/tex] é o resto da divisão de [tex]a[/tex] por [tex]m.[/tex]
Portanto, os inteiros [tex]a~[/tex] e [tex]~b[/tex] deixam o mesmo resto quando divididos por [tex]m.[/tex]
(ii) Suponhamos agora que [tex]a~[/tex] e [tex]~b[/tex] deixam o mesmo resto [tex]r[/tex] quando divididos por [tex]m.[/tex]
Então, existem inteiros [tex]q_1[/tex] e [tex]q_2[/tex] tais que:
[tex]\qquad a=mq_1+r[/tex], com [tex]0 \leq r \lt m[/tex]
e
[tex]\qquad b=mq_2+r[/tex], com [tex]0 \leq r \lt m.[/tex]
Portanto, segue que:
[tex]\qquad a-b=\left(m q_1+r\right)-\left(mq_2+r\right)\\
\qquad a-b=m q_1+r-mq_2-r\\
\qquad a-b=m\left(q_1-q_2\right).[/tex]
Como [tex]q_1-q_2 \in \mathbb{Z}[/tex], então [tex]m \mid (a-b)[/tex] e, por definição, [tex]a\equiv b \,(\text{mod}\,m).[/tex]
Podemos, então, utilizar duas caracterizações de inteiros côngruos [tex]a~[/tex] e [tex]~b[/tex]; quais sejam:
[tex]\quad \rhd a~[/tex] é congruente a [tex]~b[/tex] módulo [tex]m[/tex] se, e somente se, [tex]m[/tex] divide a diferença [tex]a-b.[/tex]
[tex]\quad \rhd a~[/tex] é congruente a [tex]~b[/tex] módulo [tex]m[/tex] se, e somente se, [tex]a~[/tex] e [tex]~b[/tex] deixam o mesmo resto quando divididos por [tex]m.[/tex]
A seguir, vamos apresentar propriedades que poderão nos ajudar nas nossas discussões.
Algumas propriedades
Vamos apresentar a seguir algumas propriedades da relação de congruência. Cada uma delas está ilustrada por um pequeno exemplo. Para fins de simplificação, vamos assumir que os números com os quais estamos lidando sejam sempre inteiros e, particularmente o inteiro [tex]m[/tex] seja positivo ([tex]m \gt 0[/tex]).
► Propriedade 1. [tex]a\equiv a \,(\text{mod}\,m).[/tex]
Como [tex]m \cdot 0=0[/tex] e [tex]a-a=0[/tex], temos que [tex]m \mid (a-a).[/tex] Logo, por definição, [tex]a\equiv a \,(\text{mod}\,m).[/tex]
Exemplo:
[tex]\boxed{2\equiv 2 \,(\text{mod}\,3)}[/tex] ([tex]2−2=3\times 0[/tex])
► Propriedade 2. Se [tex]a\equiv b \,(\text{mod}\,m)[/tex], então [tex]b\equiv a \,(\text{mod}\,m).[/tex]
Se [tex]a\equiv b \,(\text{mod}\,m)[/tex], então [tex]m \mid (a-b).[/tex] Assim, existe [tex]k \in \mathbb{Z}[/tex] tal que [tex]a-b=km.[/tex]
Dessa forma, segue que:
[tex]\qquad b-a=−(a-b)=-(km)=(-k)m[/tex], com [tex]-k \in \mathbb{Z}[/tex],
donde [tex]b\equiv a \,(\text{mod}\,m).[/tex]
Exemplo:
[tex]\boxed{15\equiv 3 \,(\text{mod}\,12)}[/tex], já que [tex] 15−3=12\times 1.[/tex]
Logo, [tex]\boxed{3\equiv 15 \,(\text{mod}\,12)}.[/tex]
► Propriedade 3. Se [tex]a\equiv b \,(\text{mod}\,m)[/tex] e [tex]b\equiv c \,(\text{mod}\,m)[/tex], então [tex]a\equiv c \,(\text{mod}\,m).[/tex]
Se [tex]a\equiv b \,(\text{mod}\,m)[/tex] e [tex]b\equiv c \,(\text{mod}\,m)[/tex], então [tex]m \mid (a-b)~[/tex] e [tex]m \mid (b-c).[/tex]
Assim, existem inteiros [tex]k[/tex] e [tex]t[/tex] tais que [tex]a-b=km~[/tex] e [tex]~b-c=tm.[/tex]
Portanto,
[tex]\qquad a-c=(a-b)+(b-c)=km+tm=(k+t)m.[/tex]
Como [tex]z=k+t \in \mathbb{Z}[/tex], então [tex]a-c=zm[/tex], com [tex]z\in \mathbb{Z}[/tex] e, portanto, [tex]m \mid (a-c)[/tex], ou seja, [tex]a\equiv c \,(\text{mod}\,m).[/tex]
(Observe que poderíamos ter utilizado a Propriedade (*) para concluir diretamente que, se [tex]m \mid (a-b)~[/tex] e [tex]m \mid (b-c),[/tex] então [tex]m \mid \left((a-b)+(b-c)\right)[/tex] e, portanto, [tex]m \mid (a-c).[/tex])
Exemplo:
Observe que [tex]\boxed{9\equiv 5 \,(\text{mod}\,4)}~[/tex] e [tex]~\boxed{5\equiv 1 \,(\text{mod}\,4)}[/tex], pois [tex]9-5=1\times 4~[/tex] e [tex]~5-1=1\times 4[/tex].
Portanto, [tex]\boxed{9\equiv 1 \,(\text{mod}\,4)}.[/tex]
► Propriedade 4. Se [tex]a\equiv b \,(\text{mod}\,m)[/tex] e [tex]n \gt 0[/tex] é um inteiro tal que [tex]n \mid m[/tex], então [tex]a\equiv b \,(\text{mod}\,n).[/tex]
Se [tex]a\equiv b \,(\text{mod}\,m)[/tex], então [tex]m \mid (a-b)~[/tex] e, com isso, existe um inteiro [tex]k[/tex] tal que [tex]a-b=km.[/tex]
Por outro lado, se [tex]n \mid m[/tex], com [tex]n \gt 0[/tex], então existe um inteiro [tex]t[/tex] de modo que [tex]m=tn.[/tex]
Fazendo as devidas substituições, temos [tex]a-b=(kt)n[/tex], como [tex]kt \in \mathbb{Z}.[/tex] Portanto [tex] n \mid (a-b)[/tex], donde segue que [tex]a\equiv b \,(\text{mod}\,n).[/tex]
Exemplo:
Como [tex]\boxed{9\equiv 1 \,(\text{mod}\,4)}[/tex], pois [tex]9-1=2\times 4~[/tex], e [tex]\boxed{2 \mid 4}[/tex], então [tex]\boxed{9\equiv 1 \,(\text{mod}\,2)}.[/tex]
► Propriedade 5. Se [tex]a\equiv b \,(\text{mod}\,m)[/tex] e [tex]c\equiv d \,(\text{mod}\,m)[/tex], então:
(i) [tex](a+c)\equiv (b+d) \,(\text{mod}\,m).[/tex]
(ii) [tex]ac\equiv bd \,(\text{mod}\,m).[/tex]
Se [tex]a\equiv b \,(\text{mod}\,m)[/tex] e [tex]c\equiv d \,(\text{mod}\,m)[/tex], então [tex]m \mid (a-b)~[/tex] e [tex]m \mid (c-d).[/tex]
Assim, existem inteiros [tex]k[/tex] e [tex]t[/tex] tais que [tex]a-b=km~[/tex] e [tex]~c-d=tm.[/tex]
Dessa forma:
(i) [tex](a+c)-(b+d)=(a-b)+(c-d)=km+tm\\
\qquad \qquad \qquad \quad =(k+t)m=zm,[/tex]
com [tex]z=k+t \in \mathbb{Z}~~[/tex] e, portanto, [tex]m \mid [(a+c)-(b+d)][/tex].
Logo, por definição de congruência, [tex](a+c)\equiv (b+d) \,(\text{mod}\,m).[/tex]
(Aqui também poderíamos ter utilizado a Propriedade (*) e, de [tex]m \mid (a-b)~[/tex] e [tex]m \mid (c-d)[/tex], concluir diretamente que [tex]m \mid \left((a-b)+(c-d)\right)[/tex] e, como isso, [tex]m \mid \left((a+c)-(b+d)\right).[/tex]
(ii) [tex]ac-bd=ac-ad+ad-bd=a(c-d)+d(a-b)=a(tm)+d(km)=\\
\qquad \qquad \qquad=(at+dk)m=ym,[/tex]
com [tex]y=at+dk \in \mathbb{Z}.[/tex]
Logo, [tex]m \mid (ac-bd)[/tex] e, portanto, [tex]ac\equiv bd \,(\text{mod}\,m).[/tex]
Exemplo:
Veja que [tex]\boxed{9\equiv 6 \,(\text{mod}\,3)}~[/tex] e [tex]~\boxed{5\equiv 2 \,(\text{mod}\,3)}[/tex], pois [tex]9-6=1\times 3~[/tex] e [tex]~5-2=1\times 3[/tex].
Logo, [tex]\boxed{(9+5)\equiv (6+2) \,(\text{mod}\,3)}~[/tex] e [tex]\boxed{(9\times 5)\equiv (6\times 2) \,(\text{mod}\,3)}~[/tex], isto é, [tex]\boxed{14 \equiv 8 \,(\text{mod}\,3)}~[/tex] e [tex]\boxed{45 \equiv 12 \,(\text{mod}\,3)}.[/tex]
► Propriedade 6. Sejam [tex]a[/tex], [tex]b[/tex], [tex]m[/tex] e [tex]n[/tex] inteiros positivos.
Se [tex]a\equiv b \,(\text{mod}\,n)[/tex], então [tex]a^m\equiv b^m \,(\text{mod}\,n).[/tex]
Se [tex]a\equiv b \,(\text{mod}\,n)[/tex], temos que [tex] n \mid (a-b)[/tex], ou seja, existe um inteiro [tex]k[/tex] de modo que [tex]a-b=kn.[/tex]
Pela identidade algébrica
[tex]\quad a^m-b^m=(a-b)\left(a^{m-1}+a^{m-2}b+a^{m-3}b^2+\cdots +ab^{m-2}+b^{m-1}\right),[/tex]
podemos concluir que
[tex]\quad a^m-b^m=n\left(k\left(a^{m-1}+a^{m-2}b+a^{m-3}b^2+\cdots +ab^{m-2}+b^{m-1}\right)\right).[/tex]
Como [tex]a[/tex], [tex]b[/tex], [tex]m[/tex] e [tex]k[/tex] são inteiros positivos, então [tex]a^m-b^m=nt[/tex], com
[tex]\quad k\left(a^{m-1}+a^{m-2}b+a^{m-3}b^2+\cdots +ab^{m-2}+b^{m-1}\right)=t \in \mathbb{Z}.[/tex]
Então, [tex]n \mid a^m-b^m[/tex], donde concluímos que [tex]a^m\equiv b^m \,(\text{mod}\,n).[/tex]
Exemplo:
Note que [tex]\boxed{7\equiv 3 \,(\text{mod}\,4)}[/tex], pois [tex]7-3=1\times 4.[/tex]
Portanto, por exemplo,
[tex]\boxed{7^2\equiv 3^2 \,(\text{mod}\,4)}[/tex], ou seja, [tex]49\equiv 9 \,(\text{mod}\,4).[/tex]
[tex]\boxed{7^3\equiv 3^3 \,(\text{mod}\,4)}[/tex], ou seja, [tex]343\equiv 27 \,(\text{mod}\,4).[/tex]
[tex]\boxed{7^5\equiv 3^5 \,(\text{mod}\,4)}[/tex], ou seja, [tex]16807\equiv 243 \,(\text{mod}\,4).[/tex]
Exercícios de Fixação
Que tal alguns exercícios antes de prosseguir?
O que procuramos para a solução do problema é o valor de [tex]x[/tex], [tex]0\leq x \lt 7[/tex], para o qual [tex]100\times 101\times 102≡ x \,(\text{mod}\,7).[/tex]
Como [tex]100\equiv 2 \,(\text{mod}\,7)[/tex], pela Propriedade 5, temos que, [tex]\left(100+1\right)\equiv \left(2+1\right) \,(\text{mod}\,7)[/tex] e, então, [tex]101\equiv 3 \,(\text{mod}\,7)[/tex].
Da mesma forma, temos [tex]102\equiv 4 \,(\text{mod}\,7).[/tex]
Ainda pela Propriedade 5, temos:
[tex]\qquad 100\times 101\times 102\equiv 2\times 3\times 4\,(\text{mod}\,7)[/tex],
donde [tex]100\times 101\times 102\equiv 24\,(\text{mod}\,7)[/tex], ou ainda, [tex]100\times 101\times 102\equiv 3\,(\text{mod}\,7)[/tex], uma vez que [tex]24\equiv 3\,(\text{mod}\,7).[/tex]
Portanto, o resto na divisão de [tex] 100\times 101\times 102[/tex] por [tex]7[/tex] é [tex]3.[/tex]
Sabemos que [tex]34≡ 1 \,(\text{mod}\,11)[/tex]; portanto, pela Propriedade 6, temos que, [tex]34^2\equiv 1^2 \equiv 1\,(\text{mod}\,11).[/tex]
Além disso, pela Propriedade 1, [tex]5≡ 5 \,(\text{mod}\,11).[/tex]
Logo, pela propriedade 5,segue que:
[tex]\qquad 34^2 \times 5\equiv 1 \times 5 \equiv 5\,(\text{mod}\,11).[/tex]
Portanto, o resto na divisão de [tex] 34^2\times 5[/tex] por [tex]11[/tex] é [tex]5.[/tex]
Sabemos que [tex]16≡ 2 \,(\text{mod}\,7)[/tex]; portanto, pela Propriedade 6, temos que, [tex]16^{100}\equiv 2^{100} \,(\text{mod}\,7).[/tex]
Agora, resta-nos encontrar o resto na divisão de [tex]2^{100}[/tex] por [tex]7.[/tex]
Note que podemos encontrar um padrão nas divisões das potências de [tex]2[/tex] por [tex]7[/tex]; observe:
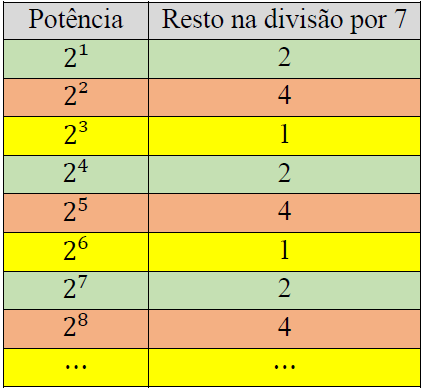
- Perceba que, para cada expoente que pode ser escrito como [tex]3n[/tex], sendo [tex]n[/tex] um valor inteiro positivo, [tex]2^{3n}[/tex] terá resto [tex]1[/tex] na divisão por [tex]7[/tex], como indicado em amarelo na tabela. Para todo número da forma [tex]3n+1[/tex], [tex]2^{3n+1}[/tex] terá resto [tex]2[/tex]; e, para todo número da forma [tex]3n+2[/tex], [tex]2^{3n+2}[/tex] terá resto [tex]4.[/tex]
Como [tex]100[/tex] é escrito na forma [tex]\boxed{3n+1}[/tex] ([tex]3\times 33+1=100[/tex]), temos que o resto da divisão solicitada é [tex]2.[/tex]
Classes Residuais e Aritmética Modular
Considerando, por exemplo, a divisão euclidiana de números inteiros por 2, o conjunto [tex] \mathbb{ℤ}[/tex] pode ser particionado em dois subconjuntos disjuntos: o dos números que deixam resto 0 na divisão por 2 (conjunto dos números pares) e o dos números que deixam resto 1 na divisão por 2 (conjunto dos números ímpares).
No estudo que estamos iniciando, esses dois conjuntos receberão nomes e notações especiais; respectivamente:
● classe residual módulo [tex]2[/tex] do número inteiro [tex]0[/tex], denotada por [tex]\overline{0}[/tex]
● classe residual módulo [tex]2[/tex] do número inteiro [tex]1[/tex], denotada por [tex]\overline{1}.[/tex]
Assim, só para ir nos acostumando com os novos conceitos, temos que:
[tex]\qquad \{\cdots -4,-2,0,2,4,6 \cdots \}=\{x \in \mathbb{Z}~;~x\equiv 0 \,(\text{mod}\,2)\}=\overline{0} [/tex]
[tex]\qquad \{\cdots −3,−1,1,3,5,7 \cdots \}=\{x \in \mathbb{Z}~;~x\equiv 1 \,(\text{mod}\,2)\}=\overline{1}.[/tex]
De forma análoga, considerando a divisão euclidiana de números inteiros por 5, outro exemplo, [tex]\mathbb{Z}[/tex] pode ser particionado em cinco subconjuntos: os subconjuntos disjuntos dos números que deixam resto 0, 1, 2, 3 e 4 quando divididos por 5.
Assim, fixada a congruência módulo 5, teremos: [tex]\mathbb{Z}= \overline{0} \cup \overline{1} \cup \overline{2} \cup \overline{3} \cup \overline{4}.[/tex]
Os subconjuntos [tex] \overline{0} \,;\, \overline{1} \,;\, \overline{2} \,;\, \overline{3} \,;\, \overline{4}[/tex] são igualmente denominados classes residuais; mas neste caso, são classes residuais módulo 5.
Cuidado: Observe que a classe residual [tex]\overline{0}[/tex] módulo [tex]2[/tex] é diferente da classe residual [tex]\overline{0}[/tex] módulo [tex]5[/tex]; o mesmo valendo para as respectivas classes residuais [tex]\overline{1}.[/tex]
Vamos generalizar essas ideias e conceitos.
Seja [tex]a[/tex] um número inteiro. Denotaremos por [tex]\overline{a}[/tex] o conjunto de todos os inteiros [tex]b[/tex] que são congruentes a [tex]a[/tex] módulo [tex]n[/tex]:
[tex]\qquad \overline{a}=\{b \in \mathbb{Z} \mid b\equiv a \,(\text{mod}\,n)\}.[/tex]
Esse conjunto será denominado classe residual de [tex]a[/tex] módulo [tex]n[/tex], ou simplesmente a “classe de [tex]a[/tex]”, se o módulo [tex]n[/tex] estiver fixado.
Observe que no conjunto [tex]\overline{a}[/tex] estarão todos os inteiros [tex]b[/tex] tais que [tex]n \mid (a-b)[/tex]; portanto, se [tex]b \in \overline{a}[/tex], [tex]a[/tex] e [tex]b[/tex] têm o mesmo resto quando divididos por [tex]n.[/tex] Dessa forma, se o resto da divisão de [tex]a[/tex] por [tex]n[/tex] for [tex]r[/tex], todos os elementos de [tex]\overline{a}[/tex] quando divididos por [tex]n[/tex] deixam resto [tex]r.[/tex]
Sabemos que as possibilidades para o resto de uma divisão por [tex]n[/tex] são [tex]0,\,1,\,2,\,\cdots\,, n-1[/tex], então temos [tex]n[/tex] classes residuais módulo [tex]n[/tex] e, portanto, conseguimos particionar o conjunto dos números inteiros em [tex]n[/tex] subconjuntos não vazios e disjuntos dois a dois: o “subconjunto dos inteiros que quando divididos por [tex]n[/tex] deixam resto [tex]0[/tex]”; o “subconjunto dos inteiros que quando divididos por [tex]n[/tex] deixam resto [tex]1[/tex]”; o “subconjunto dos inteiros que quando divididos por [tex]n[/tex] deixam resto [tex]2[/tex]”; [tex] \cdots[/tex]; o “subconjunto dos inteiros que quando divididos por [tex]n[/tex] deixam resto [tex]n-1[/tex]”.
Em símbolos:
[tex]\qquad \{x \in \mathbb{Z}~\mid~x\equiv 0 \,(\text{mod}\,n)\}[/tex];
[tex]\qquad \{x \in \mathbb{Z}~\mid~x\equiv 1 \,(\text{mod}\,n)\}[/tex];
[tex]\qquad \{x \in \mathbb{Z}~\mid~x\equiv 2 \,(\text{mod}\,n)\}[/tex];
[tex]\qquad \qquad \vdots[/tex]
[tex]\qquad \{x \in \mathbb{Z}~\mid~x\equiv (n-1) \,(\text{mod}\,n)\}.[/tex]
Como estamos agrupando os números inteiros de acordo com o restos de uma divisão por [tex]n[/tex] e cada um desses conjuntos é uma classe residual módulo [tex]n[/tex], podemos utilizar a seguinte notação para esses conjuntos:
[tex]\qquad \overline{0}=\{x \in \mathbb{Z}~\mid~x\equiv 0 \,(\text{mod}\,n)\}[/tex];
[tex]\qquad \overline{1}=\{x \in \mathbb{Z}~\mid~x\equiv 1 \,(\text{mod}\,n)\}[/tex];
[tex]\qquad \overline{2}=\{x \in \mathbb{Z}~\mid~x\equiv 2 \,(\text{mod}\,n)\}[/tex];
[tex]\qquad \qquad\vdots[/tex]
[tex]\qquad \overline{n-1}=\{x \in \mathbb{Z}~\mid~x\equiv (n-1) \,(\text{mod}\,n)\}[/tex].
Se [tex]n=4[/tex], por exemplo, a partição dos inteiros nos quatro subconjuntos disjuntos pode ser assim ilustrada:
[tex] \qquad \begin{array}{r |r |r | r}
\vdots &\vdots & \vdots & \vdots\\
-8 & -7 &-6 & -5\\
-4 & -3 & -2 & -1\\
0 & 1 & 2 & 3 & \\
4 & 5 & 6 & 7\\
\vdots &\vdots & \vdots & \vdots\\
\end{array}[/tex]
e a formalização poderia ser esta:
[tex]\qquad \overline{0}=\{x \in \mathbb{Z}~\mid~x\equiv 0 \,(\text{mod}\,4)\}[/tex];
[tex]\qquad \overline{1}=\{x \in \mathbb{Z}~\mid~x\equiv 1 \,(\text{mod}\,4)\}[/tex];
[tex]\qquad \overline{2}=\{x \in \mathbb{Z}~\mid~x\equiv 2 \,(\text{mod}\,4)\}[/tex];
[tex]\qquad \overline{3}=\{x \in \mathbb{Z}~\mid~x\equiv 3 \,(\text{mod}\,4)\}[/tex].
Mas nada impediria que esses quatro conjuntos fossem assim nomeados:
[tex]\qquad \overline{8}=\{x \in \mathbb{Z}~\mid~x\equiv 0 \,(\text{mod}\,4)\}[/tex];
[tex]\qquad \overline{17}=\{x \in \mathbb{Z}~\mid~x\equiv 1 \,(\text{mod}\,4)\}[/tex];
[tex]\qquad \overline{26}=\{x \in \mathbb{Z}~\mid~x\equiv 2 \,(\text{mod}\,4)\}[/tex];
[tex]\qquad \overline{43}=\{x \in \mathbb{Z}~\mid~x\equiv 3 \,(\text{mod}\,4)\}[/tex].
Qualquer número que pertença a uma classe residual poderá ser utilizado para representá-la, de acordo com a seguinte observação:
[tex]\qquad \overline{a}= \overline{b}\Leftrightarrow a\equiv b \,(\text{mod}\,n)\Leftrightarrow [/tex]
[tex]\qquad \Leftrightarrow a\text{ e } b \text{ deixam o mesmo resto quando divididos por } n.[/tex]
Particularmente, quando uma classe residual módulo [tex]n[/tex] está representada na forma [tex]\overline{a} [/tex] com [tex]0 \leq a \lt n-1[/tex], dizemos que ela está na forma reduzida.
Pelo exposto, [tex]\mathbb{Z}[/tex] pode ser particionado em [tex]n[/tex] subconjuntos: as classes residuais [tex]\overline{0},\overline{1},\overline{2},\overline{3},\cdots,\overline{n-1}[/tex]. Assim,
[tex]\qquad \mathbb{Z}= \overline{0} \cup \overline{1} \cup \overline{2} \cup \cdots \cup \overline{n-1}~[/tex]
e, pela unicidade do resto na Divisão Euclidiana, esses [tex]n[/tex] conjuntos são dois a dois disjuntos.
Agora, fixado um inteiro [tex]n\gt 1[/tex], vamos definir um conjunto formado pelas [tex]n[/tex] classes residuais módulo [tex]n.[/tex] Com isso, teremos um conjunto de subconjuntos de [tex]\mathbb{Z}[/tex] que será denotado por [tex]\mathbb{Z}_n:[/tex]
[tex]\qquad \mathbb{Z}_n=\{\overline{a} \mid a\in \mathbb{Z}\}.[/tex]
Se estivermos representando as classes na forma reduzida, então:
[tex]\qquad \mathbb{Z}_n=\{\overline{0}, \overline{1}, \overline{2}, \cdots , \overline{n-1}\}.[/tex]
Perceba que o índice [tex]n[/tex] de [tex]\mathbb{Z}_n[/tex] nos dá duas informações: o módulo segundo o qual estamos considerando as classes e quantos elementos/classes tem [tex]\mathbb{Z}_n.[/tex] Por exemplo:
[tex]\qquad \mathbb{Z}_\textcolor{red}{2}[/tex] tem [tex]\textcolor{red}{2}[/tex] classes residuais módulo [tex]\textcolor{red}{2}[/tex]: [tex]\mathbb{Z}_2=\{\overline{0}, \overline{1}\}[/tex];
[tex]\qquad \mathbb{Z}_\textcolor{red}{5}[/tex] tem [tex]\textcolor{red}{5}[/tex] classes residuais módulo [tex]\textcolor{red}{5}[/tex]: [tex]\mathbb{Z}_5=\{\overline{0}, \overline{1}, \overline{2}, \overline{3}, \overline{4}\}[/tex];
[tex]\qquad \mathbb{Z}_\textcolor{red}{8}[/tex] tem [tex]\textcolor{red}{8}[/tex] classes residuais módulo [tex]\textcolor{red}{8}[/tex]: [tex]\mathbb{Z}_8=\{\overline{0}, \overline{1}, \overline{2}, \overline{3}, \overline{4}, \overline{5}, \overline{6}, \overline{7}\}.[/tex]
É sobre o conjunto [tex]\mathbb{Z}_n[/tex] que iremos definir uma Aritmética, olhando cada classe residual como um elemento ([tex]\overline{a} \in \mathbb{Z}_n[/tex]) e não como um conjunto ([tex]\overline{a} \subset \mathbb{Z}[/tex]).
Uma característica bem legal das classes residuais é que elas permitem transformar congruências em igualdades já que, fixado um número inteiro [tex]n \gt 1[/tex], as classes residuais módulo [tex]n[/tex] transformam a congruência [tex]a\equiv b \,(\text{mod}\,n)[/tex] na igualdade [tex]\overline{a}=\overline{b}[/tex].
Será que você consegue mostrar a propriedade que permite essa transformação? Que tal mostrar que [tex]a\equiv b \,(\text{mod}\,n)[/tex] se, e somente se, [tex]\overline{a}=\overline{b}[/tex].
Vejamos alguns exemplos numéricos para ilustrar essa afirmação.
Em [tex]\mathbb{Z}_6[/tex]:
[tex]\quad \overline{60}=\overline{0}[/tex], pois [tex]60\equiv 0 \,(\text{mod}\,6)[/tex];
[tex]\quad \overline{604}=\overline{4}[/tex], pois [tex]604\equiv 4 \,(\text{mod}\,6)[/tex];
[tex]\quad \overline{37}\ne \overline{20}[/tex], pois [tex]37 \not \equiv 20 \,(\text{mod}\,6)[/tex], já que [tex]6 \nmid (37-20).[/tex]
Em [tex]\mathbb{Z}_9[/tex]:
[tex]\quad \overline{180}=\overline{0}[/tex], pois [tex]180\equiv 0 \,(\text{mod}\,9)[/tex];
[tex]\quad \overline{5614}=\overline{5920}[/tex], pois [tex]5614\equiv 5920 \,(\text{mod}\,9).[/tex]
Em [tex]\mathbb{Z}_{20}[/tex]:
[tex]\quad \overline{633}=\overline{433}[/tex], pois [tex]633\equiv 433 \,(\text{mod}\,20)[/tex];
[tex]\quad \overline{7201}\ne \overline{4300}[/tex], pois [tex]7201\not \equiv 4300\,(\text{mod}\,20)[/tex], já que [tex]20 \nmid (7201-4300).[/tex]
Repetindo uma observação importante: Fixado um inteiro [tex]n \gt 1[/tex], as afirmações
- [tex]\quad \rhd a\equiv b \,(\text{mod}\,n)[/tex] se, e somente se, [tex]\overline{a}=\overline{b}.[/tex]
e
[tex]\quad \rhd [/tex] Todos os possíveis restos de uma divisão por [tex]n[/tex] são os números: [tex]0,\, 1,\, 2,\,\cdots\,,\, n−1[/tex]
nos garantem que, fixado um inteiro [tex]n \gt 1[/tex], qualquer classe residual [tex]\overline{a}[/tex] é igual a uma, e somente uma, das seguintes classes: [tex]\overline{0},\,\overline{1},\,\overline{2},\,\overline{3},\,\cdots\,,\,\overline{n-1}.
[/tex]
E isso garante a nossa escolha de definir [tex]\mathbb{Z}_n[/tex] como o conjunto dessas classes!
Só tome cuidado para não confundir estas duas belas igualdades:
[tex]\qquad \rhd \mathbb{Z}= \overline{0} \cup \overline{1} \cup \overline{1} \cup \overline{2} \cup \cdots \cup \overline{n-1}~[/tex]
[tex]\qquad \rhd \mathbb{Z}_n=\{\overline{0}, \overline{1}, \overline{2}, \cdots , \overline{n-1}\}.[/tex]
E a tal Aritmética dos Restos?
Vamos fazer uma breve introdução ao estudo deste tema.
De maneira informal, a Aritmética dos números inteiros é a parte da Matemática que lida com as operações numéricas adição, subtração, multiplicação e divisão e suas consequências.
Destacamos a palavra operações, pois sem operações a Aritmética não existiria; dessa forma, o início da Aritmética Modular consiste na definição do conjunto com o qual vamos lidar e de suas operações elementares.
O conjunto já está escolhido: [tex]\mathbb{Z}_n[/tex], para [tex]n \in \mathbb{Z}[/tex], [tex]n \gt 1.[/tex]
Falta, então, a definição de operações em [tex]\mathbb{Z}_n[/tex]; e vamos definir três operações: adição, subtração e multiplicação.
Assim, vamos definir três regras que, a cada dois elementos quaisquer [tex]\overline{a}[/tex] e [tex]\overline{b}[/tex] de [tex]\mathbb{Z}_n[/tex], associam elementos de [tex]\mathbb{Z}_n[/tex] que serão denotados por [tex]\overline{a}+\overline{b}~[/tex] ; [tex]~\overline{a}-\overline{b}~[/tex] e [tex]~\overline{a}\times\overline{b}.[/tex]
Vamos lá:
[tex]\qquad \overline{a}+\overline{b}=\overline{a+b};[/tex]
[tex]\qquad \overline{a}-\overline{b}=\overline{a-b};[/tex]
[tex]\qquad \overline{a}\times\overline{b}=\overline{a\times b}.[/tex]
Observe a sutileza dessas definições:
- À esquerda temos a soma/a diferença/o produto de duas classes; à direita temos a classe da soma/da diferença/do produto de dois números inteiros.
Assim,
* estamos definindo a soma de classes, que são conjuntos, a partir de um elemento de cada conjunto;
* estamos definindo a diferença de classes, que são conjuntos, a partir de um elemento de cada conjunto;
* estamos definindo o produto de classes, que são conjuntos, a partir de um elemento de cada conjunto.
Mas quem nos garante que, escolhendo elementos diferentes de cada classe, não vamos obter um resultado diferente?
Para um melhor entendimento dessa observação, façamos um exemplo. Considere em [tex]\mathbb{Z}_{10}[/tex] as classes [tex]\overline{3}[/tex] e [tex]\overline{2}[/tex], então:
[tex]\qquad \overline{3}+\overline{2}=\overline{5};[/tex]
[tex]\qquad \overline{3}-\overline{2}=\overline{1};[/tex]
[tex]\qquad \overline{3}\times\overline{2}=\overline{6}.[/tex]
Mas como [tex]33\equiv 3 \,(\text{mod}\,10)~[/tex] e [tex]~12\equiv 2 \,(\text{mod}\,10)[/tex], então [tex]\overline{33}=\overline{3}~[/tex] e [tex]~\overline{12}=\overline{2}.[/tex] Assim, o que aconteceria se somássemos as classes [tex]\overline{33}~[/tex] e [tex]~\overline{12}[/tex]? O que aconteceria se fizéssemos a diferença das classes [tex]\overline{33}~[/tex] e [tex]~\overline{12}[/tex]? O que aconteceria se multiplicássemos as classes [tex]\overline{33}~[/tex] e [tex]~\overline{12}[/tex]?
Bem, se estamos, de fato, operando com classes, os resultados têm que ser respectivamente iguais, pois estamos operando com os mesmos conjuntos, não é?
Vejamos:
[tex]\qquad \overline{33}+\overline{12}=\overline{55};[/tex]
[tex]\qquad \overline{33}-\overline{12}=\overline{21};[/tex]
[tex]\qquad \overline{33}\times\overline{12}=\overline{396}.[/tex]
Mas sabemos que [tex]55\equiv 5 \,(\text{mod}\,10)[/tex], [tex]21\equiv 1 \,(\text{mod}\,10)[/tex] e [tex]396\equiv 6 \,(\text{mod}\,10)[/tex]; logo [tex]\overline{55}=\overline{5}[/tex], [tex]\overline{21}=\overline{1}[/tex] e [tex]\overline{396}=\overline{6}[/tex]. Portanto:
[tex]\qquad \overline{33}+\overline{12}=\overline{3}+\overline{2};[/tex]
[tex]\qquad \overline{33}-\overline{12}=\overline{3}-\overline{2};[/tex]
[tex]\qquad \overline{33}\times \overline{12}=\overline{3}\times \overline{2}.[/tex]
Ufa… E isso não acontece só para o nosso exemplo; acontece SEMPRE: os resultados definidos para as três operações entre duas classes independem dos números inteiros que utilizamos para representar essas classes!
Você pode ver a demonstração dessa afirmação clicando no próximo botão. Mas, se for mais conveniente, prossiga com a leitura e veja algumas tabelas contendo exemplos da definição das três operações.
[tex]\qquad a\equiv b \,(\text{mod}\,n)[/tex] se, e somente se, [tex]\overline{a}=\overline{b}.[/tex]
Prova:
Sejam, então, [tex]\overline{a}\,,\, \overline{a’}\,,\, \overline{b}\,,\, \overline{b’} \in \mathbb{Z}_n[/tex] tais que [tex]\overline{a}= \overline{a’}~[/tex] e [tex]\overline{b}= \overline{b’}.[/tex]
Assim, pela propriedade em destaque, [tex]a \equiv a’\,(\text{mod}\,n)~[/tex] e [tex]~b \equiv b’\,(\text{mod}\,n).[/tex]
Com isso, pela Propriedade 5, [tex](a+b) \equiv (a’+b’)\,(\text{mod}\,n)~[/tex] e [tex]~a\cdot b \equiv a’\cdot b’\,(\text{mod}\,n).[/tex]
Utilizando mais uma vez a propriedade em destaque, concluímos que [tex]\boxed{\overline{a+b}= \overline{a’+b’}}~[/tex] e [tex]\boxed{\overline{a\cdot b}= \overline{a’ \cdot b’}}.[/tex]
Então, de fato, [tex]\overline{a}+\overline{b}=\overline{a’}+\overline{b’}~[/tex] e [tex]~\overline{a} \times \overline{b}=\overline{a’}\times\overline{b’}.[/tex]
Deixamos para você a justificativa de que, nas mesmas condições, [tex]\overline{a}-\overline{b}=\overline{a’}-\overline{b’}~.[/tex]
Bom trabalho!
Como os resultados das três operações entre duas classes que definimos independem dos números inteiros que utilizamos para representar essas classes, é claro que vamos trabalhar com as representações mais simples, que são as classes residuais na forma reduzida.
►Aritmética módulo 2: [tex]\mathbb{Z}_2=\{ \overline{0}, \overline{1}\}[/tex]
[tex] \qquad \begin{array}{c|c c }
\; +& \overline{0} & \overline{1} \\
\hline
\;\overline{0}&\overline{0} & \overline{1} \\
\;\overline{1}&\overline{1} & \overline{0} \\
\end{array}[/tex][tex] \qquad \begin{array}{c|c c}
\; -& \overline{0} & \overline{1} \\
\hline
\;\overline{0}&\overline{0} & \overline{1}\\
\;\overline{1}&\overline{1} & \overline{0} \\
\end{array}[/tex][tex] \qquad \begin{array}{c|c c}
\; \times& \overline{0} & \overline{1} \\
\hline
\;\overline{0}&\overline{0} & \overline{0} \\
\;\overline{1}&\overline{0} & \overline{1} \\
\end{array}[/tex]
►Aritmética módulo 3: [tex]\mathbb{Z}_3=\{ \overline{0}, \overline{1}, \overline{2}\}[/tex]
[tex] \qquad \begin{array}{c|c c c}
\; +& \overline{0} & \overline{1} & \overline{2}\\
\hline
\;\overline{0}&\overline{0} & \overline{1} & \overline{2}\\
\;\overline{1}&\overline{1} & \overline{2} & \overline{0}\\
\;\overline{2}&\overline{2} & \overline{0} & \overline{1}\\
\end{array}[/tex][tex] \qquad \begin{array}{c|c c c}
\; -& \overline{0} & \overline{1} & \overline{2}\\
\hline
\;\overline{0}&\overline{0} & \overline{2} & \overline{1}\\
\;\overline{1}&\overline{1} & \overline{0} & \overline{2}\\
\;\overline{2}&\overline{2} & \overline{1} & \overline{0}\\
\end{array}[/tex][tex] \qquad \begin{array}{c|c c c}
\; \times& \overline{0} & \overline{1} & \overline{2}\\
\hline
\;\overline{0}&\overline{0} & \overline{0} & \overline{0}\\
\;\overline{1}&\overline{0} & \overline{1} & \overline{2}\\
\;\overline{2}&\overline{0} & \overline{2} & \overline{1}\\
\end{array}[/tex]
►Aritmética módulo 4: [tex]\mathbb{Z}_4=\{ \overline{0}, \overline{1}, \overline{2}, \overline{3}\}[/tex]
[tex] \qquad \begin{array}{c|c c c c}
\; +& \overline{0} & \overline{1} & \overline{2} & \overline{3}\\
\hline
\;\overline{0}&\overline{0} & \overline{1} & \overline{2} & \overline{3}\\
\;\overline{1}&\overline{1} & \overline{2} & \overline{3} & \overline{0}\\
\;\overline{2}&\overline{2} & \overline{3} & \overline{0} & \overline{1}\\
\;\overline{3}&\overline{3} & \overline{0} & \overline{1} & \overline{2}\\
\end{array}[/tex][tex] \qquad \begin{array}{c|c c c c}
\; -& \overline{0} & \overline{1} & \overline{2} & \overline{3}\\
\hline
\;\overline{0}&\overline{0} & \overline{3} & \overline{2} & \overline{1}\\
\;\overline{1}&\overline{1} & \overline{0} & \overline{3} & \overline{2}\\
\;\overline{2}&\overline{2} & \overline{1} & \overline{0} & \overline{3}\\
\;\overline{3}&\overline{3} & \overline{2} & \overline{1} & \overline{0}\\
\end{array}[/tex][tex] \qquad \begin{array}{c|c c c c}
\; \times& \overline{0} & \overline{1} & \overline{2} & \overline{3}\\
\hline
\;\overline{0}&\overline{0} & \overline{0} & \overline{0} & \overline{0}\\
\;\overline{1}&\overline{0} & \overline{1} & \overline{2} & \overline{3}\\
\;\overline{2}&\overline{0} & \overline{2} & \overline{0} & \overline{2}\\
\;\overline{3}&\overline{0} & \overline{3} & \overline{2} & \overline{1}\\
\end{array}[/tex]
Observe que, diferentemente da Aritmética dos números inteiros, [tex]\overline{2}\ne \overline{0}[/tex], mas [tex]\overline{2}\times \overline{2} = \overline{0}.[/tex]
►Aritmética módulo 5: [tex]\mathbb{Z}_5=\{ \overline{0}, \overline{1}, \overline{2}, \overline{3}, \overline{4}\}[/tex]
[tex] \qquad \begin{array}{c|c c c c c}
\; +& \overline{0} & \overline{1} & \overline{2} & \overline{3}& \overline{4}\\
\hline
\;\overline{0}&\overline{0} & \overline{1} & \overline{2} & \overline{3} & \overline{4}\\
\;\overline{1}&\overline{1} & \overline{2} & \overline{3} & \overline{4} & \overline{0}\\
\;\overline{2}&\overline{2} & \overline{3} & \overline{4} & \overline{0} & \overline{1}\\
\;\overline{3}&\overline{3} & \overline{4} & \overline{0} & \overline{1} & \overline{2}\\
\;\overline{4}&\overline{4} & \overline{0} & \overline{1} & \overline{2} & \overline{3}\\
\end{array}[/tex][tex] \qquad \begin{array}{c|c c c c c}
\; -& \overline{0} & \overline{1} & \overline{2} & \overline{3} & \overline{4}\\
\hline
\;\overline{0}&\overline{0} & \overline{4} & \overline{3} & \overline{2} & \overline{1}\\
\;\overline{1}&\overline{1} & \overline{0} & \overline{4} & \overline{3} & \overline{2}\\
\;\overline{2}&\overline{2} & \overline{1} & \overline{0} & \overline{4} & \overline{3}\\
\;\overline{3}&\overline{3} & \overline{2} & \overline{1} & \overline{0} & \overline{4}\\
\;\overline{4}&\overline{4} & \overline{3} & \overline{2} & \overline{1} & \overline{0}\\
\end{array}[/tex][tex] \qquad \begin{array}{c|c c c c c}
\; \times& \overline{0} & \overline{1} & \overline{2} & \overline{3} & \overline{4}\\
\hline
\;\overline{0}&\overline{0} & \overline{0} & \overline{0} & \overline{0} & \overline{0}\\
\;\overline{1}&\overline{0} & \overline{1} & \overline{2} & \overline{3} & \overline{4}\\
\;\overline{2}&\overline{0} & \overline{2} & \overline{4} & \overline{1} & \overline{3}\\
\;\overline{3}&\overline{0} & \overline{3} & \overline{1} & \overline{4} & \overline{2}\\
\;\overline{4}&\overline{0} & \overline{4} & \overline{3} & \overline{2} & \overline{1}\\
\end{array}[/tex]
Em [tex]\mathbb{Z}_5[/tex], a regra “se [tex]\overline{a} \ne \overline{0}~[/tex] e [tex]\overline{b} \ne \overline{0}[/tex], então [tex]\overline{a} \times \overline{b} \ne \overline{0}[/tex]” volta a valer.
Veja que em [tex]\mathbb{Z}_3[/tex], essa regra também vale. Mas em [tex]\mathbb{Z}_6[/tex], mesmo sem uma tabela, podemos perceber que [tex]\overline{2} \ne \overline{0}~[/tex], [tex]\overline{3} \ne \overline{0}[/tex], mas [tex]\overline{2} \times \overline{3} = \overline{0}.[/tex]
Por que será?
A esta altura do campeonato, você pode estar se perguntando: Existe divisão em [tex]\mathbb{Z}_n[/tex]?
Vamos pensar por um instante no conjunto dos números reais. Nesse conjunto, “dividir o número [tex]a[/tex] pelo número não nulo [tex]b[/tex]” é equivalente a “multiplicar o número [tex]a[/tex] pelo número [tex]1/b[/tex]”, não é?
Transpor essas ideais para [tex]\mathbb{Z}_n[/tex] não é um “bicho de sete cabeças”, mas talvez seja um “bicho com umas três ou quatro cabeças”!
Por exemplo, em [tex]\mathbb{Z}_8[/tex], [tex]\overline{2} \ne \overline{0}~[/tex], [tex]\overline{4} \ne \overline{0}[/tex], mas [tex]\overline{2} \times \overline{4} = \overline{0}.[/tex] Assim, em [tex]\mathbb{Z}_8[/tex], assim como em [tex]\mathbb{Z}_6[/tex] e em outros [tex]\mathbb{Z}_n[/tex]’s , teremos problemas para definir inversos…
Como estamos nos propondo a fazer uma apresentação inicial de [tex]\mathbb{Z}_n[/tex] e suas operações e não necessitaremos dessas informações para prosseguir com nossas discussões, deixaremos essa conversa de inversos e divisões para outra ocasião…
IV – Equações Diofantinas
O estudo de Equações Diofantinas é uma aplicação interessante do conceito de divisibilidade. Elas são equações polinomiais com coeficientes inteiros, para as quais se buscam soluções também inteiras. Além disso, as variáveis da equação podem ter grau maior do que 1, o que gera uma grande diversidade de problemas envolvendo esse tipo de equação, desde o estudo do Teorema de Pitágoras, ou seja, equações na forma [tex]a^2+b^2=c^2[/tex], até a prova do Último Teorema de Fermat (mais informações podem ser encontradas neste link). Contudo, por se tratar de um tópico introdutório às equações diofantinas, nos limitaremos nesta Sala de Estudo às equações com duas incógnitas de grau 1, ou seja, aquelas do tipo [tex] \boxed{\,ax+by=c\,}[/tex], com coeficientes [tex]a,\, b,\, c \in \mathbb{Z}[/tex] e soluções inteiras, ou seja, [tex](x,y)\in \mathbb{Z}^2.[/tex]
Observe, por exemplo, a equação [tex]2x−6y=7.[/tex]
Muitos já devem estar familiarizados com equações desse tipo e com sua representação no plano cartesiano: uma reta. Portanto, os pares [tex](x,y)\in \mathbb{R}^2[/tex] que são solução dessa equação são todos os pontos que pertencem a essa reta. No entanto, nenhuma dessas soluções é um par ordenado pertencente a [tex]\mathbb{Z}^2[/tex], pois uma soma entre dois números pares ([tex]2x[/tex] e [tex]-6y[/tex]) não pode resultar no número ímpar [tex]7.[/tex] Além disso, o que torna esse fato ainda mais interessante é a análise do gráfico da reta definida por [tex]2x−6y=7[/tex], representado na próxima figura.
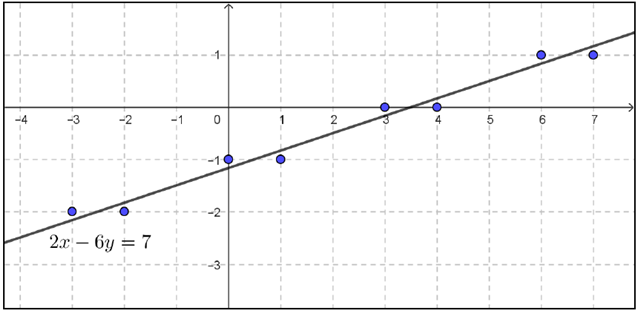
De fato, a inexistência de soluções em [tex]\mathbb{Z}^2[/tex] para a equação [tex]2x−6y=7[/tex] pode ser percebida no gráfico da imagem acima, na medida em que a reta parece “desviar” de todos os pontos com coordenadas inteiras, isto é, a reta não intercepta nenhum dos cruzamentos da malha quadriculada pontilhada da imagem.
Equações Diofantinas e Congruências
A fim de evidenciar a relevância das Equações Diofantinas em problemas do dia-a-dia, pensemos na seguinte questão:
- Visitei uma livraria que estava com uma promoção imperdível: todos os livros estavam custando R$ 10,00 ou R$ 18,00. Meus pais me deram R$ 100,00 para comprar os livros que eu quisesse. Pensando em gastar todo o dinheiro que me foi dado, quantas e quais são as maneiras que me permitem realizar essa compra?
O problema pode ser matematicamente “traduzido” pela seguinte equação diofantina: [tex]10x+18y=100[/tex], sendo [tex]x,\, y \in \mathbb{N}[/tex] ([tex]x[/tex] e [tex] y [/tex] representam quantidades). Podemos reescrever essa equação pensando em congruências módulo [tex]5[/tex]:
[tex]\qquad 10x+18y\equiv 100 \,(\text{mod}\,5)\\
\qquad 0x+3y\equiv 0 \,(\text{mod}\,5)\\
\qquad 3y\equiv 0 \,(\text{mod}\,5).[/tex]
Dessa forma, [tex]5 \mid 3y[/tex], ou seja, estamos procurando números naturais que quando multiplicados por [tex]3[/tex] sejam múltiplos de [tex]5.[/tex]
Assim, [tex]y \in \{0,5,10,15,20,\cdots\}[/tex]; em termos de congruência, isso significa que [tex]y\equiv 0 \,(\text{mod}\,5).[/tex]
A nossa equação inicial pode ser reescrita como [tex]5x+9y=50[/tex] e, para cada valor de [tex]y[/tex] encontrado, temos um valor de [tex]x[/tex] correspondente. Vamos então fazer algumas continhas.
Perceba que [tex]x \geq 0[/tex] e [tex]5x=50-9y[/tex]; logo devemos ter [tex]50-9y \geq 0[/tex], ou seja, [tex]9y \leq 50[/tex], o que acarreta [tex]y \leq 5.[/tex]
Portanto, temos apenas dois valores de [tex]y[/tex] que interessam para o problema: [tex]y=0[/tex] e [tex]y=5.[/tex]
Para [tex]y=0[/tex], obtemos [tex]x=10[/tex]; e para [tex]y=5[/tex], obtemos [tex]x=1.[/tex]
Dessa forma, posso realizar a compra dos livros somente de duas maneiras:
- “Comprando 10 livros de R$ 10,00 somente” ou “1 livro de R$ 10,00 e 5 livros de R$ 18,00”.
Observe, no entanto, que à parte do contexto de compra de livros (que exige que [tex]x[/tex] e [tex]y[/tex] sejam inteiros positivos), a equação [tex]10x+18y=100[/tex] possui infinitos pares [tex](x,y) \in \mathbb{Z}^2[/tex] como solução. Na verdade, como veremos mais adiante, isso sempre ocorre: se uma equação diofantina admite uma solução, então ela admite infinitas.
Utilizar artifícios algébricos como o apresentado acima para resolver equações diofantinas é, de fato, muito útil para a resolução delas. No entanto, será que há alguma maneira de certificarmos que dada equação possui, de fato, solução inteira, antes de tentar resolvê-la?
A resposta é afirmativa, e faremos isso usando uma ferramenta que você provavelmente já domina: o MDC – Máximo Divisor Comum.
Dessa forma, se [tex]a~[/tex] e [tex]~b[/tex] são números inteiros não simultaneamente nulos, então o [tex]mdc(a,b)[/tex] é um divisor de [tex]a~[/tex] e de [tex]~b[/tex] e é o maior dentre todos os divisores comuns de [tex]a~[/tex] e [tex]~b.[/tex]
Mais tarde, você pode visitar as nossas Salas sobre o “Algoritmo de Euclides para determinação de MDC”, clicando AQUI. Neste momento, estamos apenas interessados em encontrar um resultado que nos permita saber se uma equação diofantina tem ou não solução; e, para isso, vamos apresentar um resultado central para obter essa resposta: podemos sempre escrever o MDC entre dois inteiros como uma combinação linear entre eles.
O Teorema de Bézout afirma que “Dados [tex]a~[/tex] e [tex]~b[/tex] inteiros não simultaneamente nulos, existem inteiros [tex]x[/tex] e [tex]y[/tex] (não necessariamente positivos) tais que [tex]ax+by=mdc(a,b).[/tex]”
Se você quiser conhecer a demonstração desse resultado, é só clicar no botão abaixo; caso contrário, é só prosseguir com a leitura.
Este resultado é fácil de ser obtido utilizando a Divisão Euclidiana, apresentada no início desta Sala:
- Dados quaisquer [tex]n[/tex] e [tex]d[/tex] inteiros com [tex]d\ne 0[/tex], existem únicos inteiros [tex]q[/tex] e [tex]r[/tex] (quociente e resto, respectivamente) tais que [tex]n=q\cdot d+r[/tex], com [tex]0 \leq r \lt |d|.[/tex]
Para provar o Teorema de Bézout, dados [tex]a~[/tex] e [tex]~b[/tex] inteiros não simultaneamente nulos, vamos construir o conjunto
[tex] \qquad M(a,b)=\{ax+by \, |\, x,y \in \mathbb{Z}\}[/tex],
isto é, o conjunto de todos os inteiros que podem ser escritos como combinação linear de [tex]a~[/tex] e [tex]~b.[/tex]
Observe, inicialmente, que [tex]a \cdot a+b\cdot b=a^2+b^2[/tex]; assim [tex]a \cdot a+b\cdot b \in M(a,b) [/tex], pois é uma combinação linear positiva de [tex]a~[/tex] e [tex]~b[/tex], pois [tex]a\ne 0[/tex] ou [tex]b\ne 0[/tex] e, portanto [tex]a^2\ne 0[/tex] ou [tex]b^2\ne 0.[/tex]
Assim, existem elementos positivos em [tex] M(a,b)[/tex] e podemos tomar o menor deles: seja, então, [tex]d=ax_0+by_0[/tex] o menor elemento positivo de [tex] M(a,b).[/tex]
Mostraremos que [tex]d=mdc(a,b)[/tex] e, para isso, provaremos primeiro a seguinte afirmação: [tex]d[/tex] divide TODOS os elementos de [tex] M(a,b).[/tex]
- Com efeito, dado [tex]n=ax+by \in M(a,b)[/tex], pela Divisão Euclidiana, existem únicos [tex]q[/tex] e [tex]r[/tex] inteiros tais que [tex]n=q\cdot d+r[/tex], com [tex]0 \leq r \lt d.[/tex] Dessa forma, temos
[tex]\qquad r=n-q \cdot d\\
\qquad r=ax+by-q\left(ax_0+by_0\right)\\
\qquad r=a\left(x-qx_0\right)+b\left(y-qy_0\right),[/tex]
o que nos garante que [tex]r[/tex] é uma combinação linear de [tex]a~[/tex] e [tex]~b[/tex] e, portanto, [tex]r \in M(a,b).[/tex]
Mas como [tex]0 \leq r \lt d[/tex] e [tex]d[/tex] é o menor elemento positivo de [tex] M(a,b)[/tex], [tex]r[/tex] não pode ser positivo! Logo só resta para [tex]r[/tex] ser igual a zero.
Sendo [tex]r=0[/tex], segue de [tex]n=q\cdot d+r[/tex] que [tex]n=q\cdot d[/tex], o que significa que [tex]d[/tex] é divisor de qualquer elemento [tex]n[/tex] de [tex] M(a,b).[/tex]
Como [tex]a=a\cdot 1+b \cdot 0[/tex] e [tex]b=a\cdot 0+b \cdot 1[/tex], [tex]a~[/tex] e [tex]~b[/tex] pertencem a [tex] M(a,b)[/tex]; assim, pela afirmação acima, concluímos que [tex]d \mid a~[/tex] e [tex]~d \mid b[/tex], isto é, [tex]d[/tex] é um divisor comum de [tex]a~[/tex] e [tex]~b[/tex] e, portanto, [tex]d \leq mdc(a,b).[/tex]
Note ainda que, para todo inteiro [tex]c[/tex] tal que [tex]c \mid a~[/tex] e [tex]~c \mid b[/tex], temos que [tex]c \mid ax_0+by_0[/tex] e, portanto, [tex]c \mid d.[/tex] Particularmente, se [tex]c=mdc(a,b)[/tex], então [tex]mdc(a,b) \mid d[/tex], donde [tex]mdc(a,b) \leq d[/tex], já que ambos são positivos.
Sendo [tex]d \leq mdc(a,b)[/tex] e [tex]mdc(a,b) \leq d[/tex], necessariamente [tex]mdc(a,b)= d=ax_0+by_0[/tex] e, de fato, o [tex]mdc(a,b)[/tex] é combinação linear de [tex]a~[/tex] e de [tex]~b.[/tex]
O Teorema de Bézout tem uma importante consequência e é esse resultado que vai nos interessar no estudo das Equações Diofantinas:
Corolário do Teorema de Bézout: Sejam [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] números inteiros, com [tex]a[/tex] e [tex]b[/tex] não simultaneamente nulos.
A equação [tex]ax+by=c[/tex] admite solução em [tex]ℤ^2[/tex] se, e somente se, [tex]c[/tex] é divisível por [tex]mdc(a,b).[/tex]
Sejam [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] números inteiros, com [tex]a[/tex] e [tex]b[/tex] não simultaneamente nulos.
Supondo que a equação [tex]ax+by=c[/tex] admite solução em [tex]ℤ^2[/tex], considere o par [tex](x_0,y_0)[/tex] uma tal solução; assim, [tex]ax_0+by_0=c[/tex].
Como por definição [tex] mdc(a,b) \mid a[/tex] e [tex] mdc(a,b) \mid a[/tex], a Propriedade (*) garante que [tex] mdc(a,b) \mid \left(ax_0+by_0\right)[/tex] e, assim, [tex] mdc(a,b) \mid c.[/tex]
Por outro lado, supondo que [tex]c[/tex] seja divisível por [tex]mdc(a,b)[/tex], então existe [tex]k \in \mathbb{Z}[/tex] tal que [tex]c=k \cdot mdc(a,b).[/tex]
Com isso, pelo Teorema de Bézout, existem inteiros [tex]x_0[/tex] e [tex]y_0[/tex] tais que [tex]~ax_0+by_0=mdc(a,b).[/tex]
Multiplicando esta igualdade por [tex]k[/tex], temos
[tex]\qquad a\left(kx_0\right)+b\left(ky_0\right)=k\cdot mdc(a,b)[/tex]
e assim verificamos que existem os inteiros [tex]kx_0[/tex] e [tex]ky_0[/tex] que definem uma solução para a equação [tex]ax+by=c.[/tex]
Observe que “traduzindo” esse Corolário para o contexto de Equações Diofantinas, conseguimos o prometido critério para se decidir a existência ou não de soluções para uma Equação Diofantina:
CRITÉRIO: Sejam [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] números inteiros.
A equação diofantina linear [tex]~ax+by=c~[/tex] admite solução se, e somente se, [tex]c[/tex] é divisível por [tex]mdc(a,b).[/tex]
Vamos voltar ao que foi mencionado acima, sobre a infinidade de soluções de uma equação diofantina.
Já sabemos que a equação diofantina [tex]~ax+by=c~[/tex] terá uma solução se [tex]c[/tex] é divisível por [tex]mdc(a,b).[/tex]
Seja, então, [tex]x_0,y_0[/tex] uma solução particular para [tex]~ax+by=c.[/tex]
Para qualquer inteiro [tex]t[/tex], considere o par ordenado
[tex]\qquad (x,y)=\left(x_0-\dfrac{b}{mdc(a,b)}\cdot t\,,\,y_0+\dfrac{a}{mdc(a,b)}\cdot t\right)[/tex]
e observe, antes de mais nada, que [tex]\dfrac{b}{mdc(a,b)}[/tex] e [tex]\dfrac{a}{mdc(a,b)}[/tex] são números inteiros.
Temos, então, que:
[tex]\qquad ax+by=a\left(x_0-\dfrac{b}{mdc(a,b)}\cdot t\right)+b\left(y_0+\dfrac{a}{mdc(a,b)}\cdot t\right)\\
\qquad ax+by=ax_0-\dfrac{ab}{mdc(a,b)}\cdot t+by_0+\dfrac{ab}{mdc(a,b)}\cdot t\\
\qquad ax+by=ax_0-\cancel{\dfrac{ab}{mdc(a,b)}\cdot t}+by_0+\cancel{\dfrac{ab}{mdc(a,b)}\cdot t}\\
\qquad ax+by=ax_0+by_0\\
\qquad \boxed{\,ax+by=c\,}.[/tex]
Assim, para cada valor inteiro [tex]t[/tex], o par ordenado [tex]\left(x_0-\dfrac{b}{mdc(a,b)}\cdot t\,,\,y_0+\dfrac{b}{mdc(a,b)}\cdot t\right)[/tex]
fornece uma solução para a equação [tex]~ax+by=c.[/tex]
Portanto, havendo infinitos valores possíveis para [tex]t[/tex], temos infinitas soluções possíveis para a equação diofantina [tex]~ax+by=c.[/tex]
V – Alguns Problemas…
[tex]\quad Dia~atual+1\,000\equiv Dia~da~semana \,(\text{mod}\,7)[/tex].
sendo que [tex]”Dia~atual”=3[/tex] e 1 000 é o número de dias que queremos avançar.
Então,
[tex]\quad 3+1\,000=1\, 003\equiv 2\,(\text{mod}\,7)[/tex]
e isso significa que, após 1 000 dias, o aniversário de João cairá no dia 2 da semana, isto é, segunda-feira.
Porém, ainda temos que considerar 0,5 de um dia (metade de um dia), o que corresponde a 12 horas, que deverão ser adicionadas ao horário das 14h30min.
Então, a música tocará às 02h30min.
Se você calculasse [tex]n^3-n^2[/tex], você encontraria um número cujo algarismo das unidades é:
A) 0
B) 2
C) 4
D) 6
E) 8
[tex]\quad 9867\equiv 7 \,(\text{mod}\,10)\quad \textcolor{#6fa34c}{(i)}[/tex]
[tex]\quad 9867^2\equiv 7^2 \,(\text{mod}\,10).\quad \textcolor{#6fa34c}{(ii)}[/tex]
Como [tex]7^2=49~[/tex] e [tex]~49\equiv 9 \,(\text{mod}\,10)[/tex], temos que:
[tex]\quad 9867^2\equiv 9 \,(\text{mod}\,10).\quad \textcolor{#6fa34c}{(iii)}[/tex]
A partir das propriedades anteriormente definidas e das congruências [tex]\textcolor{#6fa34c}{(i)}[/tex] e [tex]\textcolor{#6fa34c}{(ii)}[/tex], segue que:
[tex]\quad 9867^3=9867^2 \times 9867\equiv 9 \times 7 \,(\text{mod}\,10).[/tex]
Mas [tex]9\times 7 =63~[/tex] e [tex]~63\equiv 3 \,(\text{mod}\,10)[/tex]; assim segue que
[tex]\quad 9867^3\equiv 3 \,(\text{mod}\,10).\quad \textcolor{#6fa34c}{(iv)}[/tex]
Das congruências [tex]\textcolor{#6fa34c}{(iii)}[/tex] e [tex]\textcolor{#6fa34c}{(iv)}[/tex], temos [tex]98673−98672\equiv 3-9 \,(\text{mod}\,10)[/tex]; no entanto, [tex]-6\equiv 4 \,(\text{mod}\,10)[/tex], então obtemos [tex]98673−98672\equiv 4 \,(\text{mod}\,10).[/tex]
Portanto, o algarismo das unidades é 4, o que torna a alternativa “C” a resposta correta.
[tex]\quad 2011^{2012}−1=\left(2011^{1006}−1\right)\cdot \left(2011^{1006}+1\right)\\
\quad \boxed{2011^{2012}−1=\left(2011^{503}−1\right)\cdot \left(2011^{503}+1\right)\cdot \left(2011^{1006}+1\right)}.[/tex]
Como [tex]2011\equiv -1 \,(\text{mod}\,4)[/tex], temos que:
[tex]\quad \left(2011^{1006}+1\right)\equiv \left((-1)^{1006}+1\right)\,(\text{mod}\,4)\\
\quad \left(2011^{1006}+1\right)\equiv 2 (\text{mod}\,4)\qquad \textcolor{#6fa34c}{(i)}[/tex]
e
[tex]\quad \left(2011^{503}-1\right)\equiv \left((-1)^{503}-1\right)\,(\text{mod}\,4)\\
\quad \left(2011^ {503}-1\right)\equiv -2 (\text{mod}\,4)\\
\quad \left(2011^ {503}-1\right)\equiv 2 (\text{mod}\,4).\qquad \textcolor{#6fa34c}{(ii)}[/tex]
Observe também que [tex]2011\equiv 3 \,(\text{mod}\,8)[/tex], logo:
[tex]\qquad 2011^{503}\equiv 3^{503} \,(\text{mod}\,8)\\
\qquad 2011^{503}\equiv \left(3^2\right)^{251}\cdot 3 \,(\text{mod}\,8)\\
\qquad 2011^{503}\equiv \left(1\right)^{251}\cdot 3 \,(\text{mod}\,8)\\
\qquad \left(2011^{503}+1\right)\equiv \left( 3+1\right) \,(\text{mod}\,8)\\
\qquad \left(2011^{503}+1\right)\equiv 4 \,(\text{mod}\,8).\qquad \textcolor{#6fa34c}{(iii)}[/tex]
Olhando as congruências [tex] \textcolor{#6fa34c}{(i)}[/tex], [tex]\textcolor{#6fa34c}{(ii)}[/tex] e [tex]\textcolor{#6fa34c}{(iii)}[/tex] sob o ponto de vista da divisibilidade temos que: [tex]4 \mid \left(2011^{1006}+1\right)-2[/tex], [tex]4 \mid \left(2011^{503}-1\right)-2[/tex] e [tex]8 \mid \left(2011^{503}+1\right)-4.[/tex]
Assim, existem inteiros [tex]t\,, k\,, z[/tex] tais que: [tex]\left(2011^{1006}+1\right)-2=4t[/tex], [tex]\left(2011^{503}-1\right)-2=4k~[/tex] e [tex]~\left(2011^{503}+1\right)-4=8z.[/tex]
Vamos analisar essas últimas igualdades:
- De [tex]\left(2011^{1006}+1\right)-2=4t[/tex] segue que
[tex]\quad \left(2011^{1006}+1\right)=2(2t+1)= 2t_1[/tex], sendo [tex]t_1[/tex] um número ímpar. - De [tex]\left(2011^{503}-1\right)-2=4k~[/tex] segue que
[tex]\quad \left(2011^{503}-1\right)=2(2k+1)= 2k_1[/tex], sendo [tex]k_1[/tex] um número ímpar. - De [tex]\left(2011^{503}+1\right)-4=8z~[/tex] segue que
[tex]\quad \left(2011^{503}+1\right)=4(2k+1)= 2^2z_1[/tex], sendo [tex]z_1[/tex] um número ímpar.
Dessa forma,
[tex]\quad \left(2011^{1006}+1\right)\cdot \left(2011^{503}-1\right) \cdot \left(2011^{503}+1\right)=2^4\cdot\left( t_1 \cdot k_1 \cdot z_1\right)\\
\quad \boxed{\left(2011^{1006}+1\right)\cdot \left(2011^{503}-1\right) \cdot \left(2011^{503}+1\right)=2^4\cdot m}[/tex]
sendo [tex]m[/tex] um inteiro ímpar.
Portanto
[tex]\quad \boxed{2011^{2012}−1=2^4\cdot m}[/tex], com [tex]m[/tex] um inteiro ímpar
o que nos permite concluir que a maior potência de [tex]2[/tex] que divide [tex]\boxed{2011^{2012}−1}[/tex] é [tex]2^4.[/tex]
Daí, [tex]p^2\equiv 1 \,(\text{mod}\,3)~[/tex] e segue que [tex]\boxed{3 \mid p^2-1}.[/tex]
Além disso, sendo [tex]p=2k+1[/tex], para algum [tex]k \in \mathbb{Z}[/tex] sabemos que
[tex]\quad p^2=\left(4k(k+1)+1\right)\equiv 1 \,(\text{mod}\,8)[/tex],
pois o produto [tex]k(k+1)[/tex] é par; e, portanto, [tex]\boxed{8 \mid p^2-1}.[/tex]
Como [tex]mdc(8,3)=1[/tex] e ambos dividem [tex]p^2-1[/tex], segue que [tex] 24 \mid p^2-1.[/tex]
Se [tex]N=4444^{4444}[/tex], [tex]A=s(n)~[/tex] e [tex]~B=S(A)[/tex], quanto vale [tex]S(B)[/tex]?
[tex]\qquad N\equiv A\equiv B \equiv s(B)\,(\text{mod}\,9).[/tex]
Inicialmente, calcularemos o resto de [tex]N[/tex] na divisão por [tex]9.[/tex] Para isso observe que, como [tex]4444\equiv 16 \equiv 7\,(\text{mod}\,9)[/tex],
então [tex]4444^{4444}\equiv 7^{4444}\,(\text{mod}\,9)[/tex] e, portanto, precisamos encontrar o resto da divisão de [tex]7^{4444}[/tex] por [tex]9.[/tex]
Note que [tex]343=7^3\equiv 1 \,(\text{mod}\,9)[/tex] e, pela divisão euclidiana, [tex]4444=1481\times 3+1[/tex]; assim, segue que:
[tex]\qquad 7^{4444}=7^{1481\times 3+1}=\left(7^3\right)^{1481}\times 7\equiv 7 \,(\text{mod}\,9)[/tex]
e, portanto, [tex]N=4444^{4444}\equiv 7 \,(\text{mod}\,9).[/tex]
Perceba, então, que [tex]\boxed{s(B)\equiv B\equiv A \equiv N \equiv 7 \,(\text{mod}\,9)}.[/tex]
Nosso próximo passo é estimar o valor de [tex]B.[/tex] Observe, inicialmente, que
[tex]\qquad N=4444^{4444}\lt 10000^{4444}=10^{4 \times 4444}=10^{17776}.[/tex]
Então [tex]A=s(N)[/tex] é a soma de, no máximo, [tex]17776[/tex] dígitos e, como o maior digito possível é [tex]9[/tex], concluímos que
[tex]\qquad A=s(N)\lt 9 \cdot 17776=159\,984.[/tex]
Dessa forma, [tex]B=s(A)[/tex] é a soma de, no máximo, [tex]6[/tex] dígitos: o primeiro é no máximo [tex]1[/tex] e, os demais, no máximo [tex]9.[/tex] Segue, então, que
[tex]\qquad B=s(A)\leq 1+5 \cdot 9=46.[/tex]
Por fim, dentre os inteiros positivos até 46, a maior soma possível de dígitos é [tex]12[/tex], ou seja, [tex]s(B)\leq 12.[/tex]
E sendo [tex]s(B)\equiv 7 \,(\text{mod}\,9)[/tex], o único valor possível para [tex]s(B)[/tex] é [tex]7.[/tex]
VI – Criptografia: uma Aplicação Interessante
 Imagem extraída de Kaspersky.
Imagem extraída de Kaspersky.
Atualmente, uma das grandes aplicações da Aritmética Modular no dia a dia é na criptografia – a ciência que tem como objeto de estudo a codificação e decodificação de mensagens e outras informações por meio de algoritmos, no intuito de proteger dados.
A codificação de uma mensagem se dá por meio de uma correspondência biunívoca entre todos os grafemas (letras) usados na mensagem e um conjunto finito e sequencial que será a mensagem codificada. Assim, ela se torna ilegível para aqueles que não possuem a sua “chave”, ou seja, a informação restrita que controla toda a operação dos algoritmos de criptografia.
Para explicar como se dá essa relação, podemos analisar um exemplo bastante conhecido na área:
Então, por exemplo, Bob começa enviando a Alice os números primos [tex]7[/tex] e [tex]11:[/tex]
o [tex]7[/tex] será a “base de uma potência”: [tex]7^x[/tex]; e o [tex]11[/tex] será “o módulo de uma congruência”: [tex]\text{mod}\,11[/tex].
Estes dois números são públicos.
- Alice, então, escolhe um número, digamos [tex]x_A=3[/tex] e, sem contá-lo a ninguém, nem mesmo para Bob, ela resolve a congruência [tex]7^{x_A}\equiv y_A \,(\text{mod}\,11)[/tex], encontrando [tex]y_A=2.[/tex]
O número [tex]2[/tex] é enviado publicamente a Bob. - Ao mesmo tempo, Bob também escolhe um número, sem contar para ninguém. Supondo que Bob tenha escolhido [tex]x_B=5[/tex], ele resolve [tex]7^{x_B}\equiv y_B \,(\text{mod}\,11)[/tex], encontrando [tex]y_B=10.[/tex]
O número [tex]10[/tex] é enviado a Alice, também publicamente. - A seguir, Alice e Bob calculam, respectivamente, [tex]y_B^{x_A}\,(\text{mod}\,11)[/tex] e [tex]y_A^{x_B}\,(\text{mod}\,11)[/tex] e o resultado encontrado será a chave que o casal utilizará para codificar suas mensagens. Para o caso que exemplificamos, temos:
Alice: [tex]10^3\equiv 10 \,(\text{mod}\,11)[/tex]
Bob: [tex]5^2\equiv 10 \,(\text{mod}\,11).[/tex]
Perceba que para os dois o resultado foi o mesmo; e um não conhecia o número secreto do outro!
Isso acontecerá para quaisquer escolhas de [tex]x_A~[/tex] e [tex]~x_B[/tex] e, para entender o motivo, vamos analisar o processo que ocorreu.
O cálculo que Alice realizou pode ser reescrito da seguinte maneira:
[tex]\qquad y_B^{x_A}=10^3\equiv \left(7^5\right)^3\,(\text{mod}\,11)[/tex]
E o cálculo que Bob realizou pode ser reescrito da seguinte maneira:
[tex]\qquad y_A^{x_B}=2^5\equiv \left(7^3\right)^5\,(\text{mod}\,11).[/tex]
Como [tex]\left(7^5\right)^3=\left(7^3\right)^5[/tex], é claro que os números [tex]y_B^{x_A}[/tex] e [tex]y_A^{x_B}[/tex] são congruentes, módulo [tex]11[/tex], e por isso Alice e Bob obtiveram o mesmo resultado.
Esse método é seguro porque, para alguém diferente de Alice e Bob descobrir a chave utilizada, seria necessário antes descobrir os números [tex]x_A[/tex] e [tex]x_B[/tex] que Bob e Alice pensaram. Mas tudo o que essa pessoa saberia a respeito desses números seriam suas congruências módulo [tex]11.[/tex] No entanto, como existem infinitos números congruentes a [tex]2[/tex] e [tex]10[/tex] módulo [tex]11[/tex], seria necessário fazer várias tentativas para conseguir, de fato, chegar a cada número pensado pelo casal.
É claro que partimos de números pequenos para deixar claro o processo que tecnicamente pode ser utilizado para números com muiiiiiiiiitos dígitos.
A chave que foi obtida pelo casal Alice e Bob pode ser utilizada de várias maneiras para codificar uma mensagem. Uma forma simples poderia ser a seguinte:
- Cada letra da mensagem original corresponderia à letra a 10 posições adiante no alfabeto, ou seja, A corresponderia a K, B corresponderia a L, e assim em diante. Se relacionássemos cada letra do alfabeto com um número:
1 ↔ A, 2 ↔ B, …, 25 ↔ Y, 26 ↔ Z,
então esse código poderia ser descrito pela seguinte função:
número original + chave = número codificado.
No caso de Alice e Bob,
número original + 10 = número codificado.
Por fim, o uso da Aritmética Modular na criptografia não se limita apenas à comunicação. Atualmente, esse sistema é utilizado para guardar senhas e arquivos na Internet, além de garantir a segurança de transações bancárias. Vale ressaltar que os números utilizados nesses casos possuem dezenas ou centenas de algarismos, o que torna praticamente impossível a quebra dessa criptografia por “hackers” ou meios tradicionais utilizando computadores. O exemplo explicado acima é apenas uma forma simples de estabelecer a relação entre criptografia e Aritmética Modular, pois da mesma forma que Bob e Alice esconderam sua chave secreta a partir de uma chave pública que não apresentava riscos, os vários sistemas computacionais podem usufruir dessa mesma técnica, porém com variações numéricas mais complexas.
COM Geomestres Slay (Colégio Militar de Porto Alegre, RS)
Equipe COM – OBMEP
Maio de 2024.
[1] HEFEZ, A. Elementos de Aritmética. 2ª Edição. Rio de Janeiro: SBM, 2005.
[2] ALEX, Carlos. Introdução à Aritmética Modular – OBM. (Acesso em 05/05/2024)
[3] BARROS, Marco Antonio de Oliveira. Aritmética Modular: Aplicações no Ensino Médio – Profmat. (Acesso em 05/05/2024)
[4] GARBI, Carlos. A Matemática Grega em uma Casca de Noz – RPM 51. (Acesso em 05/05/2024)
[5] LIMA, Yuri Gomes. CONGRUÊNCIAS – OBM. (Acesso em 05/05/2024)
[6] 140 – Aritmética Modular e Criptografia – YouTube. (Acesso em 05/05/2024)
[6] Aritmética dos restos – Portal da OBMEP. (Acesso em 05/05/2024)
