Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 6º ano do E. F. – Nível de dificuldade: Médio)
Três letreiros luminosos acendem e apagam com intermitências de [tex]36[/tex], [tex]42[/tex] e [tex]54[/tex] segundos, respectivamente.
Sabendo que esses letreiros acenderam simultaneamente às [tex]21[/tex] horas e [tex]52[/tex] minutos, qual será o próximo horário no qual os letreiros voltarão a acender juntos?

Lembretes
✐ Uma das maneiras de se obter o [tex]mmc[/tex] de dois ou mais números naturais é escrever cada número como produto de fatores primos e lembrar que:
- O [tex]mmc[/tex] de dois ou mais números é o produto dos fatores primos que aparecem na decomposição de cada número, com cada fator primo elevado ao maior dos expoentes que aparecem nessas decomposições.
✐ Podemos também obter o [tex]mmc[/tex] de dois ou mais números naturais pelo processo da decomposição simultânea, que nos dá diretamente o [tex]mmc[/tex].
Solução
Precisamos calcular inicialmente o intervalo de tempo entre dois acendimentos simultâneos desses letreiros. Em seguida, aplicar esse tempo ao horário das [tex]21[/tex] horas e [tex]52[/tex] minutos.
Vamos aproveitar e calcular esse [tex]mmc[/tex] das duas formas indicadas nos Lembretes, para recordar os dois processos.
| Fatoração isolada de [tex]36[/tex], [tex]42[/tex] e [tex]54[/tex] em fatores primos:
[tex]\;\begin{array}{r|l } Como |
Processo da decomposição simultânea de [tex]36[/tex], [tex]42[/tex] e [tex]54[/tex]:
[tex]\;\begin{array}{r r r |l} Assim, |
Portanto, de qualquer forma, os letreiros acendem simultaneamente a cada [tex]756[/tex] segundos.
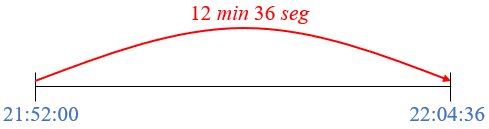
[tex]\textcolor{#800000}{(2)}[/tex] Assim, depois que os letreiros acenderam simultaneamente às [tex]21[/tex] horas e [tex] \, 52[/tex] minutos, eles voltarão a acender juntos [tex]756[/tex] segundos depois.
Para somar esses [tex]756[/tex] segundos ao último horário em que os letreiros acenderam simultaneamente, vamos calcular quantos minutos equivalem a [tex]756[/tex] segundos. Para isso, vamos fazer a divisão de [tex]756[/tex] por [tex]60[/tex]:
|
[tex]\qquad \qquad \begin{array}{r} 756\end{array} \begin{array}{|r} 60 \\ \hline \end{array}[/tex] [tex]\qquad \qquad\begin{array}{r} \underline{156} \end{array}\begin{array}{r} 12 \end{array}[/tex] [tex]\qquad \qquad\begin{array}{r} 36 \end{array}\begin{array}{r} \, \end{array}[/tex] |
Já temos que [tex]756[/tex] segundos equivalem a [tex]12[/tex] minutos e [tex]36[/tex] segundos; então, vamos à soma:
[tex]\begin{array} {r r r l} |
Finalmente, observe que [tex]64[/tex] minutos equivalem a [tex]1[/tex] hora e [tex]4[/tex] minutos; assim, depois das [tex]21[/tex] horas e [tex]52[/tex] minutos, os letreiros voltarão a acender juntos às [tex]\fcolorbox{black}{#eee0e5}{$\text{22 horas, 4 minutos e 36 segundos}$}.[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
