Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 2ª série do E. M. – Nível de dificuldade: Médio)
Edu desenhou a figura abaixo e pediu para a sua irmã Aninha pintá-la de modo que se duas regiões são vizinhas (têm uma fronteira em comum), então essas regiões devem ser pintadas com cores diferentes.
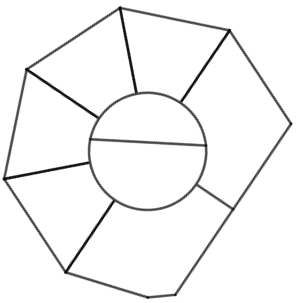
Qual o número mínimo de cores que Aninha poderá utilizar, de modo que ela possa pintar as oito regiões do desenho de acordo com a regra que Edu estabeleceu?
Solução
Para facilitar o entendimento da solução que apresentaremos, identificaremos cada uma das oito regiões do desenho feito pelo Edu, conforme mostra a próxima figura.
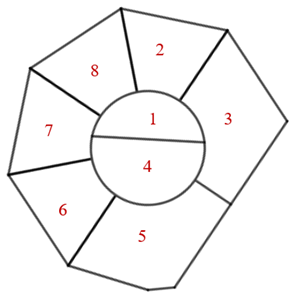
- Veja que as regiões [tex]1, 2, 3[/tex] são vizinhas entre si; assim, precisaremos de três cores diferentes para pintá-las, digamos cores [tex]A, B, C.[/tex]
Então, vamos tentar pintar as outras cinco regiões utilizando apenas essas três cores.
- A região [tex]4[/tex] é vizinha das regiões [tex]1[/tex] e [tex]3[/tex], logo devemos pintá-la com a cor [tex]B[/tex].
- A região [tex]5[/tex] é vizinha das regiões [tex]3[/tex] e [tex]4[/tex], logo devemos pintá-la com a cor [tex]A[/tex].
- A região [tex]6[/tex] é vizinha das regiões [tex]4[/tex] e [tex]5[/tex], logo devemos pintá-la com a cor [tex]C[/tex].
- A região [tex]8[/tex] é vizinha das regiões [tex]1[/tex] e [tex]2[/tex], logo devemos pintá-la com a cor [tex]C[/tex].
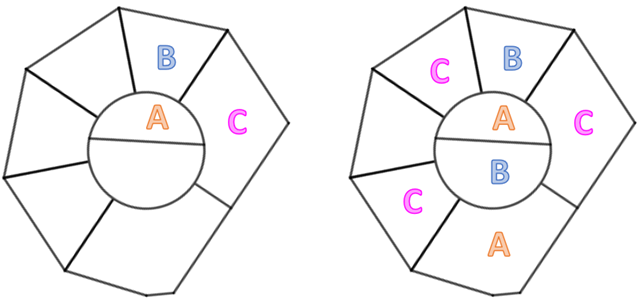
Perceba que ficamos com um problema:
- A região [tex]7[/tex] é vizinha das regiões [tex]1[/tex], [tex]4[/tex], [tex]6[/tex] e [tex]8[/tex]; logo, não podemos pintá-la com nenhuma das três cores que estamos tentando utilizar e, portanto, precisaremos de uma quarta cor: a cor [tex]D[/tex].
A figura abaixo mostra que é possível Aninha colorir o desenho de Edu, de modo que duas regiões vizinhas tenham cores diferentes, utilizando apenas quatro cores.
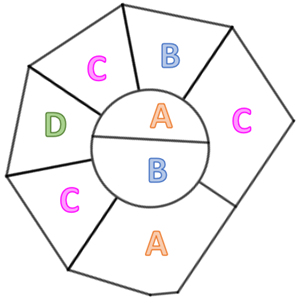
Essa não é a única maneira de pintar o desenho com 4 cores. Mas qualquer outro modo de pintá-lo irá exigir, pelo menos, quatro cores.
Solução elaborada pelos Moderadores do Blog.
Aprendendo um pouco mais – O Problema das Quatro Cores

O Problema das Quatro Cores trata da determinação do número mínimo de cores necessárias para colorir um mapa, de forma que países com fronteira comum tenham cores diferentes.
Esse problema virou o Teorema das Quatro Cores:
Todo mapa pode ser colorido com quatro ou menos cores, respeitando-se a condição de que países vizinhos, com alguma fronteira em comum, tenham cores diferentes.
Se você se interessou pelo assunto, leia estes dois textos:
- História do problema das quatro cores – Professora Milene Maria Drumond Pimenta.
- Quatro Cores e Matemática – Professor João Carlos V. Sampaio; DM, UFSCAR.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
