Assim como o jogo da Torre de Hanói, outro famoso jogo de lógica e raciocínio é o Jogo dos Jarros. Entretanto, diferentemente da Torre de Hanói, encontrar uma solução ótima, isto é, o menor número de jogadas necessárias para esse, jogo passa pelo conhecimento de uma área diferente e não muito conhecida da Matemática, a qual será objeto de atenção nesta Sala.
A versão tradicional do Jogo dos Jarros consiste em 3 jarros d’água, estando um deles cheio e os outros dois vazios. O objetivo é, a partir da transferência do líquido entre os jarros, obter uma quantidade exata de líquido pré-determinada.
O primeiro desafio imposto pelo jogo é assumir que os jarros são irregulares e não possuem qualquer tipo de marcação. Dessa maneira, não podemos encher propositalmente, por exemplo, metade ou um terço de um jarro, de modo que devemos usar como referência somente a capacidade conhecida dos jarros.
Apesar de sua origem desconhecida, o estudo analítico do Jogo dos Jarros e suas variações têm conexões com um tema pouco abordado em aulas de matemática do ensino básico, apesar de ser amplamente explorado em olimpíadas de conhecimento mais avançadas: a Teoria de Grafos. Se você não sabe o que é um grafo, não se preocupe, você vai conseguir fazer as atividades. Além disso, com certeza você vai entender a breve apresentação que dele faremos, no material que disponibilizaremos.
Jogo dos Jarros: os recipientes não possuem qualquer marcação.
 Imagem extraída do site wikiHow. (Acesso em 02/02/2024.)
Imagem extraída do site wikiHow. (Acesso em 02/02/2024.)
I – O Jogo dos Jarros tradicional: Objetivo, Ações e Regras
 Objetivo:
Objetivo:
Obter em algum dos três jarros uma quantidade de água pré-determinada.
Ações permitidas:
Transferir água de um jarro preenchido parcial ou completamente a um jarro vazio ou parcialmente preenchido.
Regras:
1. A quantidade de água disponível no início do jogo se mantém até o final: nenhuma quantidade de líquido pode ser obtida nem perdida.
2. O despejo da água de um jarro para outro só é permitido quando o jarro que recebe fica cheio ou quando o jarro que transfere fica vazio. Assim:
2.1 Caso uma parte da água contida em um jarro maior seja derramada em um jarro de menor capacidade, este deve ser preenchido completamente e a água restante deve permanecer no jarro maior.
2.2 Caso a água contida em um jarro menor seja derramada em um jarro de maior capacidade, o jarro menor deve ser esvaziado completamente ou o jarro maior deve ficar completamente preenchido.
3. Não há marcações nos jarros: em hipótese alguma deve-se medir a quantidade de água de qualquer um dos jarros. Só é permitido preencher um jarro até sua capacidade total ou despejar o conteúdo total de um jarro em outro.
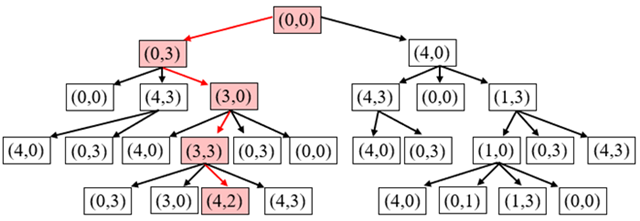
Suponha um jarro A de 8 L (cheio), um jarro B de 5 L (vazio) e um jarro C de 3 L (vazio), e chamemos essa configuração inicial de C0=[8,0,0].
Nosso objetivo é, a partir das regras acima, obter 4 L de água (objetivo) em algum dos três jarros. Pelas ações permitidas, podemos inicialmente despejar, por exemplo, 5 L em B, de modo a ficarmos com a configuração C1=[3,5,0] de litros de água nos jarros A, B e C, respectivamente.
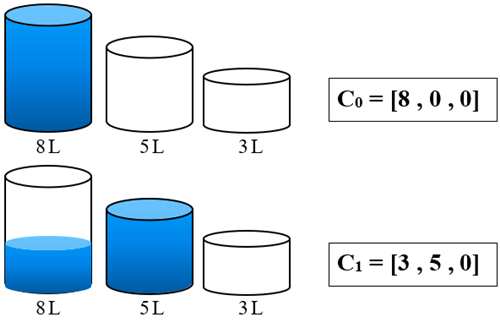
A exemplo do movimento efetuado acima, devemos encontrar uma sucessão de ações que nos permita chegar a uma configuração Cn=[4 , x , 4−x], ou alguma outra permutação dessa tripla.
II – Mãos à Obra!
Se você quiser realmente pôr a mão na massa, tente jogar o jogo com recipientes de verdade! Eles não precisam ter necessariamente capacidades de 3, 5 e 8 litros, basta que tenham capacidades proporcionais a 3, 5 e 8. Uma alternativa interessante é utilizar garrafas pet:
● Garrafa pet de 500 ml;
● Garrafa pet de 1 L;
● Garrafa pet de 1,5 L;
● Caneta permanente;
● Tesoura;
● Copo graduado (medidor de líquido);
● Pia com água à disposição.(Use, mas não desperdice!)
Como fazer:
- 1. Utilize a tesoura para recortar os bicos das garrafas para facilitar a entrada e saída de água (não hesite em chamar um adulto para ajudar);
2. Encha a garrafa de 1,5 L com 1,2 L de água (isto é, 8×150); encha a garrafa de 1 L com 750 ml de água (isto é, 5×150); encha a garrafa de 500 ml com 450 ml de água (isto é, 3×150 );
3. Utilize a caneta permanente para fazer a correta marcação dessas alturas da água nas respectivas garrafas;
4. Esvazie as duas garrafas menores e mantenha a garrafa maior com água até a marcação feita à caneta.
5. Preparado o espaço, vamos às atividades!
III – Para quem não quer se sujar…
Se você não quiser construir a sua própria versão do Jogo dos Jarros, você pode jogá-lo on-line. Confira as três versões abaixo disponibilizadas.
Mas antes de você jogar, uma observação: o objetivo final dessa versão do jogo é dividir os 8 litros de água em duas jarras de 4 litros cada. Assim, para você receber o PARABÉNS do aplicativo, alcançado o objetivo de obter 4 litros em uma das jarras, você deverá fazer mais um passo e colocar 4 litros em duas jarras.
Quando terminar de jogar, não se esqueça de fechar a janelinha que se abriu.
As duas próximas versões apresentam um visual mais simples, mas são igualmente eficazes.
➤ Nesta segunda versão, você pode escolher as capacidades em litros dos três jarros e também a quantidade de litros a ser obtida em algum dos três jarros. Para isso, clique Definir: os controles de definição tornam-se editáveis para que você possa modificar a capacidade de cada jarro ou redefinir o volume a ser obtido em um deles. Feitos os ajustes, clique novamente em Definir para jogar. Veja o visual do jogo.
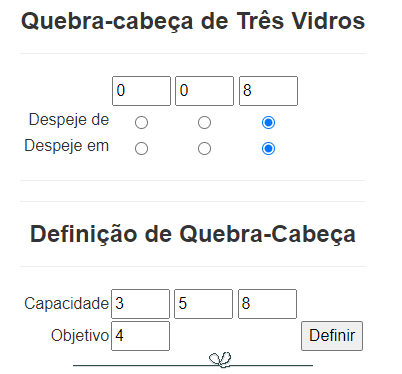
Acesse o site do jogo, clicando AQUI.
O jogo é carregado com a configuração que nos interessa, conforme mostra a figura.
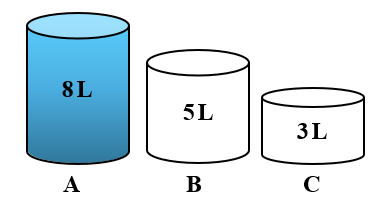
➤ A terceira versão é a mais simples. Com ela você só utiliza três jarros com capacidades de 8 L, 5L e 3L, conforme vemos na imagem a seguir.

Acesse o site do jogo, clicando AQUI.
(Os dois sites são em inglês, mas você pode ajustá-los para serem exibidos em português diretamente no seu Navegador.)
IV – Uma Variação Usual
Uma variação muito comum e que também pode ser utilizada para o estudo do Jogo dos Jarros é a versão com apenas dois jarros, com uma fonte interminável para obtenção de água e um ralo para despejamentos, de modo que possamos preencher ou esvaziar completamente os jarros sempre que necessário.
1. Preencher um jarro de água por completo;
2. Esvaziar um jarro de água por completo;
3. Transferir água de um jarro parcial ou completamente cheio para um jarro vazio ou parcialmente cheio.
Uma versão desse jogo pode ser acessada no seguinte link:
Na página do aplicativo, antes de clicar no botão Play (Jogar), você deve selecionar:
– o nível de dificuldade do jogo;
– quantos litros você deverá obter em um dos jarros;
– a quantidade de litros que cada jarro comporta.
Vale, no entanto, notar que a fonte e o ralo que aparecem nessa versão não passam de substituições do jarro de 8 da versão anterior do jogo. Analisando a solução ótima do jogo no caso {8,5,3}, notamos que a sequência de ações tomadas nesse caso é a mesma para a versão do jogo com a fonte infinita de água.
Há também variações do jogo em que a quantidade total de água contida nos três jarros é maior do que a capacidade total do maior jarro, de modo que nunca teremos dois jarros vazios. Em outras, há ainda mais jarros.
Porém, para as análises via a Teoria dos Grafos que faremos nesta Sala de Atividades, vamos nos restringir ao caso com 3 jarros.
V – Atividades com o Jogo dos Jarros
Jogo dos Jarros – caso {8, 5, 3}
Nessa tradicional configuração, o jarro A de 8 L está cheio e os jarros B e C de 5 L e 3 L, respectivamente, estão vazios. Nossa tarefa é encontrar uma sequência de ações (ou jogadas) que nos permitam obter a quantidade de 4 L em algum dos jarros, a partir das regras anteriormente estabelecidas.
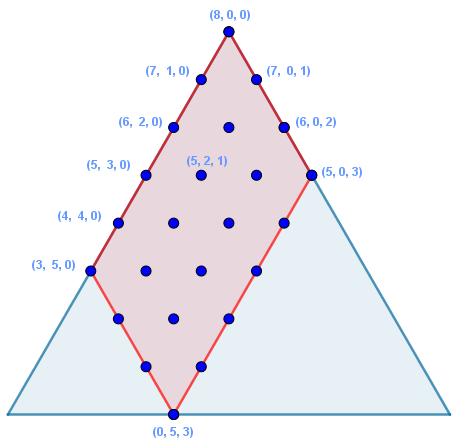
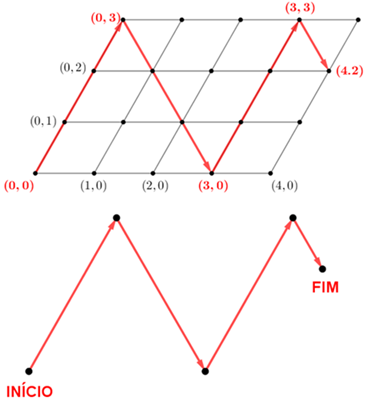
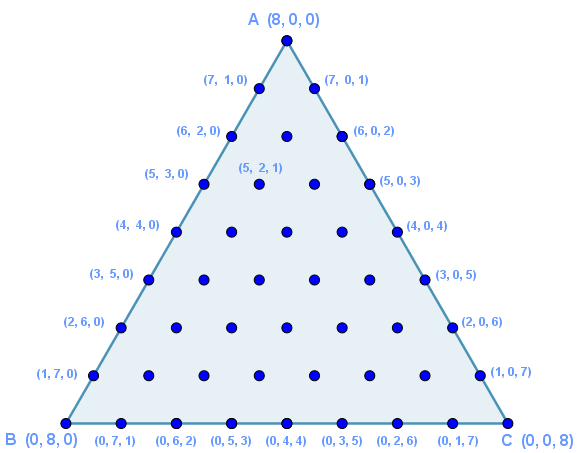
Note, por exemplo, que, partindo do estado inicial [8,0,0], que no triângulo corresponde ao vértice A cujas coordenadas são (8,0,0), ao andarmos 1 unidade para baixo sobre os lados, paramos em algum dos pontos em que o jarro A perde 1 litro (ternas (7,1,0) e (7,0,1)). De maneira similar, podemos associar a cada ponto do triângulo uma configuração (possível ou impossível) do jogo. Além disso, perceba que a quantidade de água no sistema, dada pela soma das coordenadas de cada terna, está preservada.
Assim, o ponto cujas coordenadas são (a, b, c) corresponde à configuração do jogo [a, b, c] que representa a etapa na qual o jarro A tem a litros, o jarro B tem b litros e o jarro C tem c litros.
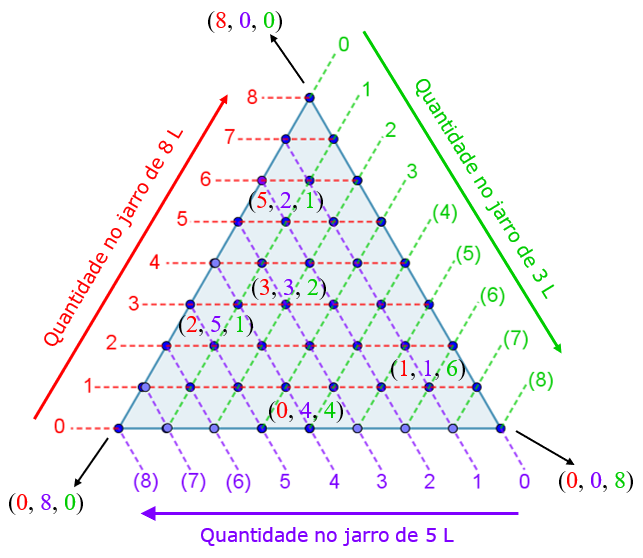
a) Quais configurações exibidas no triângulo ABC são, na verdade, impossíveis, tendo em vista a capacidade de cada jarro? Apague os pontos associados a tais configurações.
b) Apagados os pontos das configurações impossíveis, temos um novo polígono com pontos em seus lados e em seu interior. Os pontos no interior do polígono representam estados alcançáveis, tendo em vista as regras do jogo? Por quê?
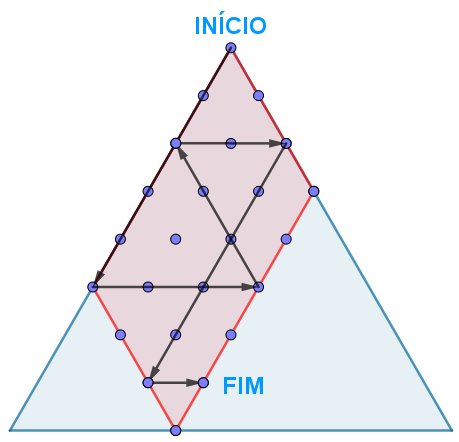
c) Agora, vamos passear por esse polígono! Você consegue encontrar uma maneira de resolver o Jogo dos Jarros utilizando os pontos do polígono construído no item a)? Qual o caminho com menor número de ações?
Para ajudar na obtenção das coordenadas dos pontos definidos a partir do triângulo ABC, utilize o esquema ilustrado na imagem a seguir.
O que você achou do diagrama construído na Atividade 7 para representar o Jogo dos Três Jarros?
Bem legal, não é?
Você sabia que esse diagrama é um exemplo de um objeto matemático?
Acompanhe no Tópico VI uma pequena apresentação desse tipo de objeto.
VI – Um pouco sobre Grafos
Informalmente, um grafo é uma estrutura matemática que descreve conexões entre objetos. É comum representarmos um grafo geometricamente e, para isso, utilizamos pontos e linhas que os conectam:
- os pontos são chamados de vértices ou nós e são utilizados na representação dos objetos;
- as linhas são chamadas de arestas ou arcos e são utilizadas para indicar a existência de conexões entre os objetos.
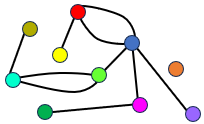
Nesses diagramas, as posições, tamanhos ou até mesmo a forma dos vértices e a forma das linhas são irrelevantes; em um grafo importa apenas “quem está ligado a quem”. Note que os dois diagramas abaixo representam o mesmo grafo.
Os grafos podem ser utilizados para representar objetos de diferentes naturezas; com isso, situações cotidianas podem ser convenientemente modeladas por meio desses diagramas contendo pontos e linhas que os conectam. Só para exemplificar, vejam algumas situações nas quais grafos podem aparecer:
- – vértices utilizados para representar pessoas e arestas para indicar quais pessoas são amigas;
– vértices utilizados para representar antenas e arestas para indicar que o sinal de uma delas pode causar interferência no sinal da outra;
– vértices utilizados para representar regiões de um mapa e arestas para indicar quais regiões possuem uma fronteira em comum;
– vértices utilizados para representar aeroportos e arestas para indicar se são oferecidos voos entre esses aeroportos;
– vértices utilizados para representar times de futebol e arestas para indicar jogos entre os times durante um campeonato;
– vértices utilizados para representar espécies animais ou vegetais e arestas para indicar se uma espécie se alimenta da outra;
– vértices utilizados para representar sistemas computacionais e arestas para indicar interconexão entre eles;
– vértices utilizados para representar páginas da Web e arestas para indicar possíveis links entre elas;
– vértices utilizados para representar as diferentes situações de um jogo e arestas para indicar possíveis passagens de uma situação para a outra.
O conceito de grafo surge a partir da abstração matemática de situações desse tipo. Sua origem é relativamente recente na história da Matemática (século XVIII); entretanto, possui grande importância não só como objeto de estudo das ciências exatas, mas também como artifício para a resolução de problemas modernos.
Esse ramo da Matemática surge com a tentativa de Leonhard Euler (1707-1783) de encontrar a solução para o seguinte problema:
É possível realizar um trajeto pelas sete pontes de Königsberg (atual Kaliningrado, na Rússia), sem cruzar nenhuma delas duas vezes?
As Sete Pontes de Königsberg
A cidade de Königsberg tinha sete pontes que conectavam as quatro áreas de terra dessa cidade cortada pelo Rio Pregel.
Pontes de Königsberg
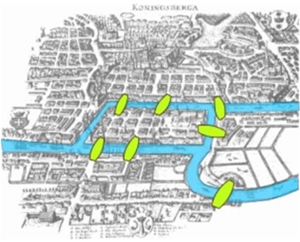 Imagem extraída da Wikipédia. (Acesso em 02/02/2024.)
Imagem extraída da Wikipédia. (Acesso em 02/02/2024.)
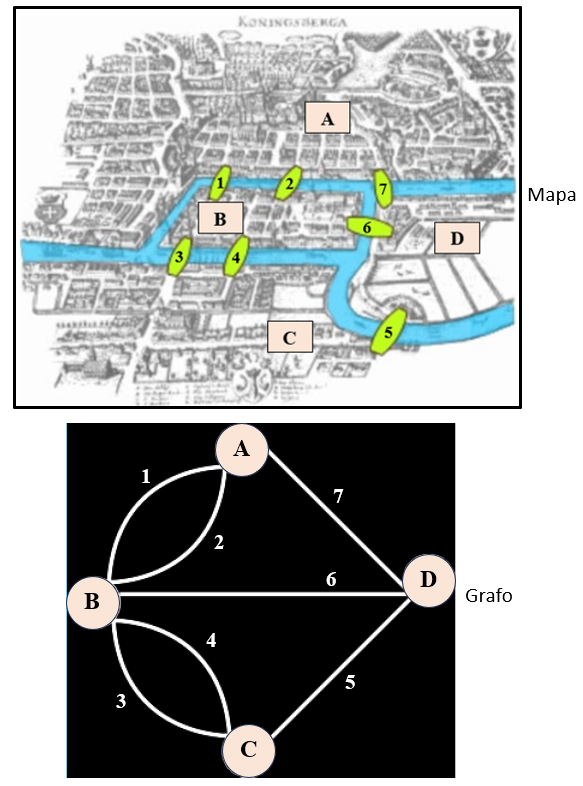
A possibilidade de atravessar cada uma das sete pontes uma única vez tornou-se uma lenda popular da cidade, até que Euler comprovou a inviabilidade desse trajeto. Euler iniciou assumindo que cada ponte só poderia ser cruzada uma única vez e que, cada vez que se entrasse numa área de terra, seria também necessário sair. Desse modo, cada área de terra precisava estar conectada por um número par de pontes, com a possível exceção do início e do fim (caso eles fossem locais diferentes). Porém, como pode ser observado nas imagens, nenhum dos pontos (ou vértices) do diagrama montado por Euler como representação do problema é o ponto final de um número par de pontes.
Ao mostrar isso, Euler forneceu o primeiro teorema da Teoria de Grafos.
Apesar da grande relevância dos trabalhos de Euler ao estudo de grafos, é apenas no século XX que a Teoria de Grafos chega à maturidade como um ramo da Matemática. O próprio termo grafo só foi cunhado em 1877, em um artigo de James Joseph Sylvester.
➤ Há vários modos de definir o conceito de grafo. Aqui nesta breve apresentação, adotaremos que um grafo é um par [tex]G=(V , E)[/tex] formado por um conjunto [tex]V[/tex] de vértices e um conjunto [tex]E[/tex] de arestas, sendo cada aresta um par não necessariamente ordenado de vértices (utiliza-se a letra E pois arestas são traduzidas como “edges” em Inglês).
Em situações particulares, é necessário modelar conexões de “um objeto para outro” e não simplesmente “entre objetos”, como no caso das Pontes. Nestes casos, arestas são definidas por pares ordenados de vértices e são representadas por setas (segmentos orientados). Esse tipo de grafo recebe a denominação de grafo orientado ou direcionado.
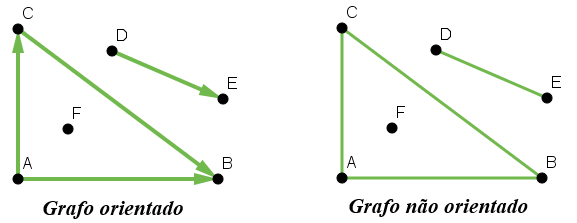
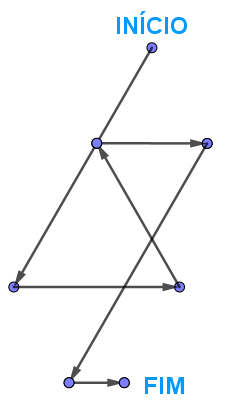
O grafo que foi construído no item c) da Atividade 7 é um exemplo de grafo orientado. Esse grafo é também um exemplo do que se denomina um grafo simples e conexo; veja as próximas definições:
- Um grafo é dito simples, se cada par de vértices corresponde a, no máximo, uma aresta e não existem arestas com vértices iguais (os chamados laços).
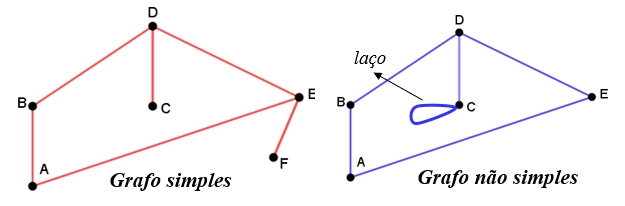
- Um grafo é dito conexo, quando qualquer par de vértices está conectado por uma sequência contínua de arestas, chamada de passeio.
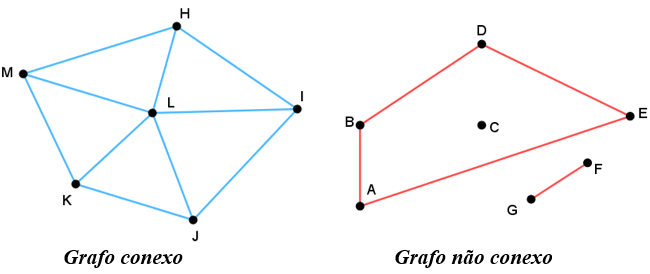
Observe que para completar o Jogo dos Jarros temos interesse em executar o menor número de jogadas. O passeio do grafo que representa esse jogo é denominado na Teoria de Grafos de caminho, isto é, um passeio por vértices todos distintos.
Voltando às pontes de Königsberg, podemos observar que o gráfico desse problema não é orientado, é conexo e não é simples (note que temos duas arestas ligando os vértices A e B, assim como duas arestas ligando os vértices B e C.)
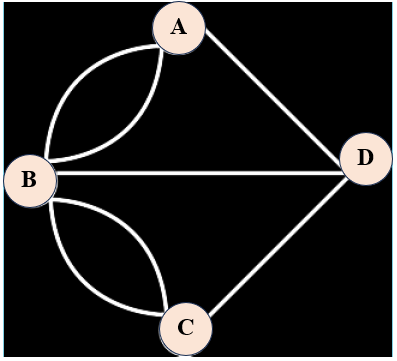
Mesmo que em situações nas quais não seja necessário utilizar resultados avançados da Teoria dos Grafos, como as apresentadas nesta Sala, a mera utilização da representação de um problema via grafos já auxilia bastante a organização das informações para a sua solução!
Lembre-se de que você pode usar uma fonte interminável para obtenção de água e um ralo para despejamentos.
VII – Jogos Impossíveis e a Aritmética
No jogo dos Jarros temos uma variedade de versões que podemos tentar atingir o objetivo final. Mesmo nos casos com dois ou três jarros, podemos alterar a capacidade de um ou todos os jarros, assim como a quantidade de água a ser obtida em um deles.
Seria interessante que a gente soubesse em que situações é teoricamente possível obtermos uma quantidade de água predeterminada para não ficar tentando encontrar uma solução que não existe.
Para os casos dos jogos com 2 ou 3 jarros já exemplificados, existe uma condição óbvia para que os jogos possam ser resolvidos com sucesso:
- 1. A quantidade de água a ser atingida deve ser menor ou igual à capacidade total de ao menos um dos jarros; pois, do contrário essa quantidade não caberia em nenhum jarro.
Temos outra?
Sim. Mas ela não é óbvia como a primeira e nem é trivial a sua justificativa:
- 2. A quantidade de água a ser atingida deve ser um múltiplo do máximo divisor comum entre a capacidade máxima de cada um dos jarros.
Antes de justificá-la, vamos tentar entender essa condição.
- Note que, no caso dos jarros de 8, 5 e 3 litros, segundo essas duas regras, seria possível alcançar qualquer quantidade de água menor do que 8 litros e múltipla do mdc(8,3,5)=1. Isso significa, então, que poderíamos obter em algum dos jarros não apenas 4 litros de água, como no exemplo proposto, mas qualquer quantidade de litros de água entre 1 e 8 (já que qualquer desses números é múltiplo de 1).
Duvidou?
Acesse o site do jogo, clicando na imagem. e observe que as capacidades 3, 5 e 8 litros já aparecerão definidas; para cada jogo, você terá apenas que definir cada objetivo: 1, 2, 3, 4, 5, 6 ou 7 litros.
 .
.
- Agora, suponha um jogo de dois jarros, com um jarro de 2 litros, outro de 4 litros, uma fonte interminável para obtenção de água e um ralo para despejamentos. Será que podemos, após realizar algumas jogadas, obter em algum jarro uma quantidade de 3 litros de água?
Pela segunda regra, a resposta é simples: NÃO!
Observe que [tex]mdc(2, 4)=2~[/tex] e 3 não é múltiplo de 2.
Duvidou?
Observe que se a resposta fosse sim, como no caso anterior, a gente poderia até demorar para fazer aparecer a quantidade de 3 litros com jarros de 2 e 4 litros; mas, obtidos os 3 litros, o problema estaria resolvido.
Agora, fazer “trocentas” tentativas e não conseguir os 3 litros, não significa que não é possível obter essa quantidade de água a partir de jarros de 2 e 4 litros. Pode ser nossa incompetência de jogar o jogo nessa versão, não é?
Para tentar justificar essa impossibilidade, vamos utilizar alguns artifícios aritméticos.
E, diferentemente da utilização de Grafos para desenhar um jogo, aqui precisaremos não apenas de uma breve introdução de um tema específico do estudo de Aritmética. Vamos precisar de dois resultados relativos à “Divisibilidade de Números Inteiros”: o Teorema de Bézout juntamente com um de seus corolários.
✶ Teorema de Bézout: Dados [tex]a[/tex] e [tex]b[/tex] inteiros positivos, existem inteiros [tex]x[/tex], [tex]y[/tex] (não necessariamente positivos) tais que [tex]ax+by=mdc(a, b).[/tex]
✶ Corolário: Dados [tex]a[/tex] e [tex]b[/tex] inteiros positivos, a equação [tex]ax+by=c[/tex], com [tex]c[/tex] também inteiro, admite solução inteira [tex](x, y ∈ \mathbb{Z})[/tex] se, e somente se, o número [tex]c[/tex] for múltiplo do [tex]mdc(a, b).[/tex]
Admitindo esses resultados, vejamos como eles se refletem no Jogo com dois Jarros de 2 e 4 litros:
- O jogo com jarros de 2 e 4 litros pode ser modelado pela equação [tex]\boxed{2x+4y=c\,}[/tex], sendo [tex]c[/tex] a quantidade que desejamos obter em algum dos dois jarros.
Uma solução [tex](x_0, y_0)[/tex] para essa equação significa que [tex]2x_0+4y_0=c\,[/tex] e pode ser interpretada como:
[tex]\quad \rhd~x_0[/tex] enchimentos via a fonte (se [tex]x_0 \gt 0[/tex]) ou esvaziamentos via o ralo (se [tex]x_0 \lt 0[/tex]) do jarro de 2 litros;
e
[tex]\quad \rhd~y_0[/tex] enchimentos via a fonte (se [tex]y_0 \gt 0[/tex]) ou esvaziamentos via o ralo (se [tex]y_0 \lt 0[/tex]) do jarro de 4 litros.
(Lembre-se de que no jogo com dois jarros usamos uma fonte interminável para obtenção de água e um ralo para despejamentos.)
Dessa forma, a quantidade só poderá ser obtida se a equação [tex]2x+4y=c[/tex] tiver soluções inteiras, o que significa [tex]c[/tex] ser múltiplo do [tex]mdc(a, b)[/tex], de acordo com o Corolário do Teorema de Bézout.
Particularmente sabemos que [tex]mdc(2, 4)=2[/tex] e [tex]3[/tex] não é múltiplo de [tex]2[/tex]; logo não conseguimos encontrar números inteiros [tex]x_0~[/tex] e [tex]~y_0[/tex] tais que [tex]2x_0+4y_0=3\,[/tex], ou seja, não podemos obter a quantidade de 3 litros d’água a partir de jarros de 2 e 4 litros.
Q u e b a c a n a, h e m ?
Vamos generalizar esse raciocínio!
A Matemática ajudando no Jogo com 2 Jarros…
Vamos admitir os dois resultados utilizados anteriormente e que serão enunciados novamente logo a seguir. Se você não sabe demonstrá-los, não faz mal: neste momento só precisamos saber utilizá-los. Mas, se você quiser ver a demonstração deles, e de outros resultados surpreendentes envolvendo Divisibilidade dos números inteiros, visite esta Sala, mais tarde.
- Teorema de Bézout: Dados [tex]a[/tex] e [tex]b[/tex] inteiros positivos, existem inteiros [tex]x[/tex], [tex]y[/tex] (não necessariamente positivos) tais que
[tex]\qquad \qquad ~~~~~~~~~~~~ax+by=mdc(a, b).[/tex] - Corolário: Dados [tex]a[/tex] e [tex]b[/tex] inteiros positivos, a equação [tex]ax+by=c[/tex], com [tex]c[/tex] também inteiro, admite solução inteira [tex](x, y ∈ \mathbb{Z})[/tex] se, e somente se, o número [tex]c[/tex] for múltiplo do [tex]mdc(a, b).[/tex]
- NOSSO PROBLEMA: Sejam [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] inteiros positivos (naturais não nulos).
A partir de dois jarros A e B com capacidade para [tex]a[/tex] e [tex]b[/tex] litros, respectivamente, de uma fonte interminável para obtenção de água e um ralo para despejamentos, é possível obter a quantidade de [tex]c[/tex] litros d’água?
O Teorema de Bézout afirma que dados [tex]a[/tex] e [tex]b[/tex] inteiros positivos, existem inteiros [tex]x[/tex], [tex]y[/tex] (não necessariamente positivos) tais que
[tex]\qquad \qquad ~~~~~~~~~~~~ax+by=mdc(a, b).[/tex]
Além disso, para os mesmos inteiros [tex]a[/tex] e [tex]b[/tex], a equação [tex]ax+by=c[/tex], com [tex]c[/tex] também inteiro, admite solução [tex](x, y)∈ \mathbb{Z}^2[/tex] (isto é, com [tex]x[/tex] e [tex]y[/tex] números inteiros) se, e somente se, o número [tex]c[/tex] for múltiplo do [tex]mdc(a, b)[/tex] (Este tipo de equação, com coeficientes inteiros e para qual se buscam soluções inteiras, é chamada de equação diofantina. ( Nesta Sala, você também poderá aprender um pouco sobre elas.)
- SOLUÇÃO DO PROBLEMA: De modo geral, se [tex]a[/tex], [tex]b[/tex] e [tex]c[/tex] são inteiros positivos (naturais não nulos), podemos obter a quantidade de [tex]c[/tex] litros d’água a partir de jarros de [tex]a[/tex] e [tex]b[/tex] litros se, e somente se, [tex]c[/tex] for múltiplo do [tex]mdc(a,b).[/tex]
a) É possível obter a quantidade de 4 litros d’água a partir de jarros de 3 e 5 litros, usando uma fonte interminável para obtenção de água e um ralo para despejamentos?
Há mais de uma possibilidade?
E 9 litros d’água a partir de jarros de 2 e 4 litros?
…E o Jogo com 3 Jarros?
A Matemática ajudando no Jogo com 3 Jarros…
Aqui, também vamos nos ater à segunda das duas condições enunciadas acima, uma vez que a primeira (A quantidade de água a ser atingida deve ser menor ou igual à capacidade total de ao menos um dos jarros.) já observamos que é simples de ser entendida.
Vamos então tratar da condição: A quantidade de água a ser atingida deve ser um múltiplo do máximo divisor comum entre a capacidade máxima de cada um dos jarros.
Admitindo uma vez mais o Teorema de Bézout e seu corolário para dois inteiros positivos [tex]a[/tex] e [tex]b[/tex] e o mdc(a, b), não é difícil demonstrar que ambos os resultados podem ser generalizados para três inteiros positivos.
Assim, se [tex]a_1[/tex], [tex]a_2[/tex] e [tex]a_3[/tex] são inteiros positivos podemos afirmar que:
- Existem inteiros [tex]x_1[/tex], [tex]x_2[/tex], [tex]x_3[/tex] (não necessariamente positivos) tais que
[tex]\qquad \qquad ~~~~~~~~~~~~a_1x_1+a_2x_2+a_3x_3=mdc(a_1, a_2, a_3).[/tex] - A equação [tex]a_1x_1+a_2x_2+a_3x_3=c[/tex], com [tex]c[/tex] também inteiro, admite solução inteira [tex](x_1, x_2, x_3 ∈ \mathbb{Z})[/tex] se, e somente se, o número [tex]c[/tex] for múltiplo do [tex] mdc(a_1, a_2, a_3)[/tex]
Mais uma vez, se você não sabe demonstrar esses resultados, não faz mal: neste momento só vamos utilizá-los para assegurar que:
- Se [tex]a_1[/tex], [tex]a_2[/tex], [tex]a_3[/tex] e [tex]c[/tex] são inteiros positivos, a partir de três jarros [tex]A_1,\, A_2,\,A_3[/tex] com capacidade para [tex]a_1[/tex], [tex]a_2[/tex] e [tex]a_3[/tex] litros, respectivamente, é possível obter a quantidade de [tex]c[/tex] litros d’água se, e somente se, [tex]c[/tex] for múltiplo do [tex]mdc(a_1,a_2,a_3).[/tex]
(Lembre-se de que no Jogo com 3 Jarros temos duas regras:
1. A quantidade de água disponível no início do jogo se mantém até o final: nenhuma quantidade de líquido pode ser obtida nem perdida.
2. O despejo da água de um jarro para outro só é permitido quando o jarro que recebe fica cheio ou quando o jarro que transfere fica vazio.)
Uma resposta mais técnica e mais completa para o jogo com três jarros pode ser encontrada no seguinte link:
Você sabia que havia tanta matemática envolvida neles?
Agora você já pode chamar seus amigos para realizar as atividades propostas! Além de poder mostrar para eles que você sabe de quantas jogadas precisa para resolver a Torre de Hanói antes mesmo de começar o jogo. Ou que sabe se uma quantidade de água no Jogo dos Jarros é viável ou não.
Demais, não é?
E nunca se esqueça:
Se quiser realizar o mínimo de jogadas, lembre-se sempre de utilizar o máximo do seu raciocínio!
COM Geomestres Slay (Colégio Militar de Porto Alegre, RS)
Equipe COM – OBMEP