Dentre lendas e potências, a torre se sustenta!
Criada em 1883 pelo matemático francês Edouard Lucas, a Torre de Hanói é um jogo muito popular entre crianças e jovens amantes da Matemática de todo o mundo. O raciocínio por trás é bastante interessante, e instigar os jovens a explorarem meios de resolver o problema da torre com êxito, ainda que realizando mais jogadas do que o mínimo necessário, é fundamental para que eles possam desenvolver suas capacidades de raciocínio lógico e criatividade.
A Torre de Hanói consiste em uma plataforma, normalmente de madeira, tradicionalmente com 3 hastes e um número determinado de discos de diâmetros diferentes, posicionados de baixo para cima, do maior para o menor.
Torre de Hanói: um dos mais conhecidos jogos na Matemática
 Imagem extraída do site Wikimedia Commons. (Acesso em 02/02/2024.)
Imagem extraída do site Wikimedia Commons. (Acesso em 02/02/2024.)
I – Salvem-se! O fim do mundo está próximo!
Segundo uma lenda hindu, na cidade santa de Benares, na Índia, debaixo da cúpula de um templo, havia uma placa de bronze e, sobre ela, três hastes de diamante fixadas. Numa dessas hastes, o deus Brahma, no momento em que criou o mundo, colocou 64 discos de ouro puro, em ordem decrescente de tamanho, de baixo para cima.
Os monges foram então instruídos a moverem a torre de discos original de uma haste a outra, utilizando uma terceira como auxiliar, sempre um disco de cada vez e nunca um disco maior sobre um disco menor. Os monges deveriam trabalhar noite e dia e, quando terminassem o trabalho, o templo seria transformado em pó e o mundo acabaria.
Ficou com medo? Não se preocupe!
Os monges precisariam realizar, no mínimo, 18.446.744.073.709.551.615 movimentos para moverem a pirâmide de uma haste a outra. Mesmo que fossem capazes de mover um disco por segundo, eles necessitariam de, aproximadamente, 585 bilhões de anos para finalmente resolverem o problema.
II – Objetivo e Regras
O objetivo do jogo Torre de Hanói, como já descrito na lenda hindu, é mover uma pilha com um número determinado de discos de uma haste a outra. As duas únicas regras para a realização dos movimentos são:
- 1. Apenas um disco pode ser transferido de uma haste a outra por vez.
2. Discos maiores não podem ser colocados sobre discos menores.
III – Mãos à obra!
Este tópico destina-se àqueles que desejam construir uma Torre de Hanói manualmente para realizarem a atividade. Caso você já possua o brinquedo, também pode utilizá-lo.
● Compasso;
● Canetas;
● Régua;
● Cola-quente;
● Papelão;
● 1 Placa de isopor;
● 3 palitos para churrasco ou canudos de plástico.
Como fazer:
1. Vamos utilizar o papelão para fazer os discos. Com o compasso, trace duas circunferências de raio 1,5 cm. Repita o procedimento, aumentando em 0,5 cm o raio das circunferências, fazendo sempre duas circunferências para cada medida de raio. Você pode fazer quantas circunferências achar necessário, porém, para uma introdução ao jogo, aconselhamos começar com 6 (3 tamanhos diferentes).
2. Recorte todos os discos e cole os de mesmo tamanho um sobre o outro, para que fiquem mais firmes.
3. Faça um furo no centro dos discos, de modo que eles possam passar com uma pequena folga pelos palitos ou canudos.
4. Finque os palitos ou canudos na placa de isopor, fixando-os com cola. É importante que a distância entre eles seja suficiente para que, na transferência das torres, um disco não colida com outro (sugerimos uma distância pelo menos igual ao diâmetro do maior disco).
5. Você já pode se divertir com a sua Torre de Hanói! Se desejar, pode ainda colorir os discos ou a base de isopor.
IV – Um aplicativo interessante
Vocês também podem utilizar o aplicativo abaixo para jogarem e se divertirem!
1) Espere o aplicativo carregar.
2) Selecione a quantidade de discos.
3) Observe a quantidade mínima de movimentos fornecida pelo aplicativo.
4) Para mover um disco, clique sobre ele e, em seguida, clique na haste para a qual ele será movido.
5) Se precisar reiniciar o jogo, clique no botão [tex]\boxed {\text{Reset}}[/tex], no canto superior esquerdo do aplicativo.
OBMEP_srdg, criado com o GeoGebra
Adaptado de: Patrícia Coelho Barbosa
V – Atividades com a Torre de Hanói
Quantos movimentos são necessários para um jogo de apenas um disco? E para um jogo de dois discos?
VI – Formalizando o Raciocínio
Conforme mencionado na resposta da Atividade 4, a quantidade mínima de movimentos necessários para mover uma torre com discos no jogo Torre de Hanói é dada pela fórmula [tex]\boxed{m(n)=2^n-1}[/tex], para todo número natural não nulo [tex]n.[/tex]
A demonstração dessa fórmula pode ser desenvolvida usando uma técnica matemática chamada Princípio da Indução Finita.
Vejamos.
- Para começar, podemos facilmente calcular que, quando [tex]n=1[/tex], a quantidade mínima de movimentos necessários é [tex]m(n)=1[/tex], já que só há um disco para mover até a haste de destino.
Aplicando [tex]n=1[/tex] na fórmula, chega-se ao resultado esperado: [tex]m(1)=2^1-1=1.[/tex] - Agora, supondo por hipótese que a fórmula seja válida para um certo número natural não nulo [tex]n[/tex], ou seja, que [tex]m(n)=2^n-1[/tex], precisamos mostrar que [tex]m(n+1)=2^{n+1}-1[/tex]
Para isso, vamos retomar uma fórmula já obtida anteriormente na Atividade 3: [tex]m\left(n\right)=2 \times m(n-1)+1.[/tex]
Substituindo [tex]n[/tex] por [tex]n+1[/tex], obtemos
[tex]\qquad m\left(n+1\right)=2 \times m((n+1)-1)+1=2 \times m(n)+1\qquad \textcolor{#4178a1}{(i)}[/tex]
e, como hipótese, [tex]\boxed{m\left(n\right)=2^n-1}[/tex], segue por [tex]\textcolor{#4178a1}{(i)}[/tex] que:
[tex]\qquad m\left(n+1\right)=2 \times \textcolor{red}{m(n)}+1\\
\qquad m\left(n+1\right)=2 \times \textcolor{red}{\left(2^n-1\right)}+1\\
\qquad m\left(n+1\right)=2^{n+1}-2+1\\
\qquad m\left(n+1\right)=2^{n+1}-1. [/tex]
Portanto, provamos que se a fórmula é verdadeira para [tex]n[/tex], então ela é também verdadeira para [tex]n+1[/tex]. Como a fórmula já foi mostrada ser verdadeira para [tex]n=1[/tex] no primeiro caso, podemos concluir que ela é verdadeira para todos os números naturais não nulos.
Observação: Para quem ficou confuso se, com as duas etapas que provamos, garantimos que a igualdade [tex]m(n)=2^n-1[/tex] é válida para todos os números naturais não nulos [tex]n[/tex], considere as seguintes afirmações utilizadas na demonstração:
(1) A igualdade [tex]m(n)=2^n-1[/tex] é válida para [tex]n=1.[/tex]
(2) Se a igualdade [tex]m(n)=2^n-1[/tex] é válida para [tex]n[/tex], então ela é também válida para [tex]n+1.[/tex]
e acompanhe alguns passos de uma sequência prática que não tem fim:
- Por (1), a igualdade em questão é válida para [tex]n=1.[/tex]
- Como a igualdade em questão é válida para [tex]n=1[/tex], por (2), ela também é válida para [tex]n=1+1=2.[/tex]
- Como a igualdade em questão é válida para [tex]n=2[/tex], por (2), ela também é válida para [tex]n=2+1=3.[/tex]
- Como a igualdade em questão é válida para [tex]n=3[/tex], por (2), ela também é válida para [tex]n=3+1=4.[/tex]
- Como a igualdade em questão é válida para [tex]n=4[/tex], por (2), ela também é válida para [tex]n=4+1=5.[/tex]
- Como a igualdade em questão é válida para [tex]n=5[/tex], por (2), ela também é válida para [tex]n=5+1=6.[/tex]
- Como a igualdade em questão é válida para [tex]n=6[/tex], por (2), ela também é válida para [tex]n=6+1=7.[/tex]
- Como a igualdade em questão é válida para [tex]n=7[/tex], por (2), ela também é válida para [tex]n=7+1=8.[/tex]
- Como a igualdade em questão é válida para [tex]n=8[/tex], por (2), ela também é válida para [tex]n=8+1=9.[/tex]
- Como a igualdade em questão é válida para [tex]n=9[/tex], por (2), ela também é válida para [tex]n=9+1=10.[/tex]
- Como a igualdade em questão é válida para [tex]n=10[/tex], por (2), ela também é válida para [tex]n=10+1=11.[/tex]
- Etc., etc., etc…
Deu para perceber que, com as duas afirmações provadas, de fato, chegamos na validade da igualdade para qualquer número natural não nulo?
VII – Aprendendo um pouco mais
Podemos também justificar que a quantidade mínima de movimentos necessários para mover os [tex]n[/tex] discos do jogo Torre de Hanói é dada pela fórmula [tex]\boxed{2^n-1}[/tex] explorando um pouco mais o conceito de “relações de recorrência”, já citado anteriormente na Atividade 3.
Uma relação de recorrência é uma relação que determina cada termo de uma dada sequência, a partir de certo termo, em função de termos anteriores; assim, uma recorrência é uma expressão que dá o valor de uma função num dado ponto em termos dos valores da mesma função em pontos anteriores.
Se você ficou curioso sobre como resolver recursivamente o jogo da Torre de Hanói para [tex]n[/tex] discos, assista o vídeo abaixo.
Antes de assisti-lo, observe e tente entender o esqueminha geométrico a seguir: ele pode ajudar…
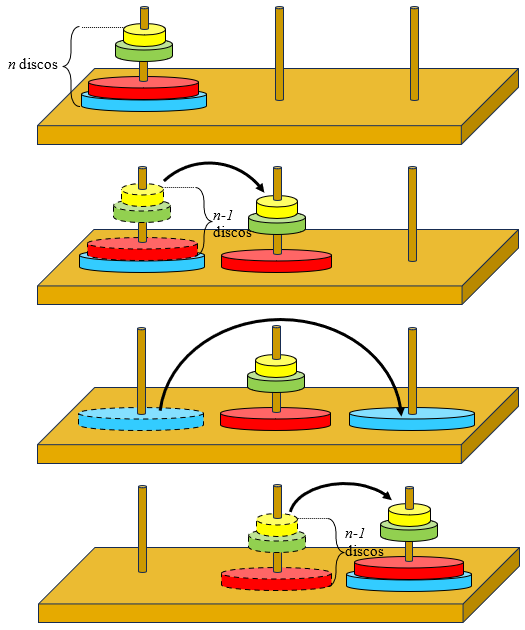
A SURPREENDENTE Matemática da TORRE de HANÓI (Fractais, Binários…)
Encontre recorrências e mais Matemática escondida na Torre de Hanói!
É só clicar na setinha.
Vídeo do canal “Tem Ciência”, de Daniel Nunes.
COM Geomestres Slay (Colégio Militar de Porto Alegre, RS)
Equipe COM – OBMEP
