Clique no botão abaixo para visualizar o problema.
Problema
(A partir da 1ª série do E. M. – Nível de dificuldade: Difícil)
(OPM – 2005) Os triângulos [tex]ABC \, [/tex] e [tex] \, EDC[/tex] mostrados na figura são retângulos, com ângulos retos em [tex]\hat{A} \, [/tex] e [tex] \, \hat{D} \, [/tex], respectivamente.
Justifique a afirmação abaixo.
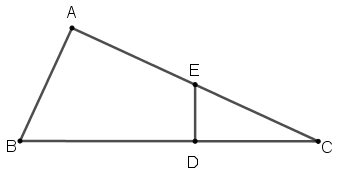
Afirmação: Se [tex]E[/tex] é o ponto médio de [tex]\overline{AC}[/tex], então o comprimento do segmento [tex]\overline{ BA}[/tex] é menor que o comprimento do segmento [tex]\overline{ BD}[/tex].
 |
Notação: Denotaremos o segmento definido por dois pontos, digamos [tex]X \, [/tex] e [tex] \, Y[/tex], por [tex]\overline {XY} [/tex] e o seu comprimento por [tex]XY[/tex]. |
Solução 1
Na figura ao lado, suponha que [tex]E[/tex] seja o ponto médio do segmento [tex]\overline{AC} \, .[/tex]
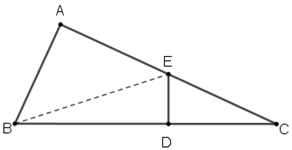
Aplicando o Teorema de Pitágoras aos triângulos retângulos [tex]BDE[/tex] e [tex]ABE[/tex] obtemos as igualdades [tex]BE^{ \, 2}=BA^{ \, 2}+AE^{ \, 2} \, [/tex] e [tex]BE^{ \, 2}=BD^{ \, 2}+DE^{ \, 2} \, [/tex], donde concluímos que:
[tex]\qquad \boxed{BA^{ \, 2}+AE^{ \, 2}=BD^{ \, 2}+DE^{ \, 2}} \, .\quad \textcolor{#800000}{(i)}[/tex]
Como [tex]E[/tex] é o ponto médio de [tex]\overline{AC}[/tex], [tex]AE=EC[/tex]; logo, segue de [tex]\textcolor{#800000}{(i)}[/tex] que:
[tex]\qquad BA^{ \, 2}+EC^{ \, 2}=BD^{ \, 2}+DE^{ \, 2} \, [/tex],
ou ainda:
[tex]\qquad \boxed{BA^{ \, 2}-BD^{ \, 2}=DE^{ \, 2}-EC^{ \, 2}} \, .\quad \textcolor{#800000}{(ii)}[/tex]
Agora, aplicando o Teorema de Pitágoras ao triângulo retângulo [tex]EDC[/tex], obtemos [tex]\boxed{EC^{ \, 2}=CD^{ \, 2}+DE^{ \, 2}} \, [/tex], donde concluímos que [tex]\boxed{EC^{ \, 2}\gt DE^{ \, 2}} \, ,[/tex] já que [tex]CD^{ \, 2}\gt 0[/tex], pois [tex]CD[/tex] é o comprimento do lado de um triângulo. Portanto:
[tex]\quad \boxed {DE^{ \, 2} – EC^{ \, 2}\lt 0} \, .\quad \textcolor{#800000}{(iii)}[/tex]
Assim,
[tex]\quad BA^{ \, 2}-BD^{ \, 2}\stackrel{\textcolor{#800000}{(ii)}}{=}DE^{ \, 2}-EC^{ \, 2}\stackrel{\textcolor{#800000}{(iii)}}{\lt} 0[/tex]
e, então, [tex] \, BA^{ \, 2}-BD^{ \, 2}\lt 0 \, .[/tex] Com isso:
[tex]\quad \left(BA+BD\right) \cdot \left(BA-BD\right) \lt 0 \, .\quad \textcolor{#800000}{(iv)}[/tex]
Mas observe que [tex]BA \, [/tex] e [tex] \, BD[/tex] são comprimentos de lados de triângulos; assim, [tex]BA+BD \gt 0[/tex]. Logo, segue de [tex]\textcolor{#800000}{(iv)}[/tex], que [tex]\boxed{BA-BD \lt 0}[/tex] e, finalmente podemos concluir que [tex] \, \fcolorbox{black}{#eee0e5}{$BA \lt BD $} \, .[/tex]
Dessa forma, o comprimento do segmento [tex]\overline{ BA}[/tex] é de fato menor que o comprimento do segmento [tex]\overline{ BD}[/tex], se [tex]E[/tex] for o ponto médio do segmento [tex]\overline{AC} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
Solução 2
Na figura abaixo, vemos em destaque os triângulos [tex]ABC \, [/tex] e [tex] \, DEC[/tex] da figura inicial do problema
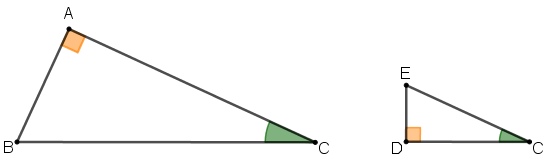
Perceba que, como os ângulos com vértices nos pontos [tex]A \, [/tex] e [tex] \, D[/tex] são ângulos retos e o ângulo com vértice em [tex]C[/tex] é comum aos dois triângulos, então [tex]ABC \, [/tex] e [tex] \, DEC[/tex] são triângulos semelhantes e, portanto,
[tex]\qquad \qquad \quad \dfrac{BC}{EC}=\dfrac{AB}{ED}=\dfrac{AC}{DC} \, .[/tex]
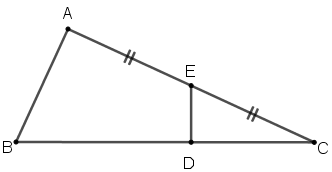
No entanto, sabemos que [tex]E[/tex] é o ponto médio do segmento [tex]\overline{AC} \, [/tex]; assim, [tex]AC =2EC \, [/tex]; logo, podemos reescrever essas igualdades da seguinte forma:
[tex]\qquad \qquad \quad \dfrac{BC}{EC}=\dfrac{AB}{ED}=\dfrac{2EC}{DC} \, .[/tex]
Com isso, segue que:
[tex] \quad 2 \, EC^{ \, 2}=BC \times DC[/tex]
[tex] \quad 2 \, EC^{ \, 2}=\left(BD+DC\right) \times DC[/tex]
[tex] \quad 2 \, EC^{ \, 2}=BD \times DC+DC^{ \, 2} \, .\quad \textcolor{#800000}{(i)}[/tex]
Aplicando o Teorema de Pitágoras ao triângulo retângulo [tex]ABC[/tex], obtemos [tex]BC^{ \, 2}=BA^{ \, 2}+AC^{ \, 2} \, [/tex], donde:
[tex] \quad BA^{ \, 2}=BC^{ \, 2}-AC^{ \, 2}[/tex]
[tex] \quad BA^{ \, 2}=\left(BD+DC\right)^{ \, 2}-AC^{ \, 2}[/tex]
[tex] \quad BA^{ \, 2}=BD^{ \, 2}+2 \, BD\times DC +DC^{ \, 2}-AC^{ \, 2}[/tex]
[tex] \quad BA^{ \, 2}=BD^{ \, 2}+2 \, BD\times DC +DC^{ \, 2}-\left(2 \, EC\right)^{ \, 2}[/tex]
[tex] \quad BA^{ \, 2}=BD^{ \, 2}+2 \, BD\times DC +DC^{ \, 2}-4 \, EC^{ \, 2}[/tex]
[tex] \quad BA^{ \, 2}=BD^{ \, 2}+2 \, BD\times DC +DC^{ \, 2}-2 \, \left(2 \, EC^{ \, 2}\right)[/tex]
[tex] \quad BA^{ \, 2}\stackrel{\textcolor{#800000}{(i)}}{=}BD^{ \, 2}+2 \, BD\times DC +DC^{ \, 2}-2 \, \left(BD \times DC+DC^{ \, 2}\right)[/tex]
[tex] \quad BA^{ \, 2}=BD^{ \, 2}+\cancel{2 \, BD\times DC }+DC^{ \, 2}-\cancel{2 \, BD \times DC}-2 \, DC^{ \, 2}[/tex]
[tex] \quad BA^{ \, 2}=BD^{ \, 2}+DC^{ \, 2}-2 \, DC^{ \, 2}[/tex]
[tex] \quad BA^{ \, 2}=BD^{ \, 2}-DC^{ \, 2} \, .\quad \textcolor{#800000}{(ii)}[/tex]
Como [tex]DC \ne 0 \, [/tex], então [tex]DC^{ \, 2} \ne 0 \, [/tex]; logo, por [tex]\textcolor{#800000}{(ii)}[/tex], podemos concluir que [tex]BA^{ \, 2}\lt BD^{ \, 2} \, [/tex], pelo que [tex]BA^{ \, 2}-BD^{ \, 2}\lt 0[/tex] e, com isso, segue que:
[tex]\qquad BA^{ \, 2} \lt BD^{ \, 2}[/tex]
[tex]\qquad \sqrt{BA^{ \, 2}} \lt \sqrt{BD^{ \, 2}} \, .\quad \textcolor{#800000}{(iii)}[/tex]
Mas observe que [tex]BA \, [/tex] e [tex] \, BD[/tex] são comprimentos de lados de triângulos; assim, [tex]BA \gt 0 \, [/tex] e [tex]BD \gt 0[/tex].
Logo, segue de [tex]\textcolor{#800000}{(iii)}[/tex] que [tex] \, \fcolorbox{black}{#eee0e5}{$BA \lt BD $} \, .[/tex]
Dessa forma, o comprimento do segmento [tex]\overline{ BA}[/tex] é de fato menor que o comprimento do segmento [tex]\overline{ BD}[/tex], se [tex]E[/tex] for o ponto médio do segmento [tex]\overline{AC} \, .[/tex]
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
