A Matemática das Alavancas – Sala 2
A Matemática e a Física das Alavancas
Para início de conversa, vamos pensar na seguinte situação:
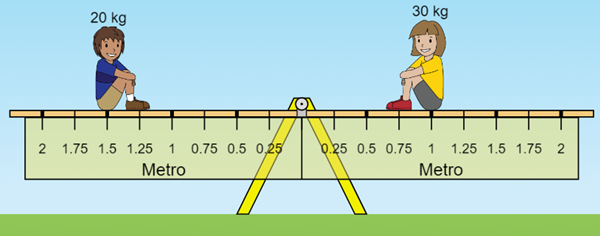
Um menino com 20 kg e uma menina com 30 Kg vão brincar em uma gangorra que inicialmente está na posição horizontal.
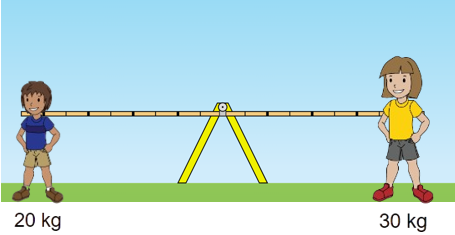
Se a menina sentar de um lado do brinquedo e o menino do outro lado, o que irá acontecer?
Você deve estar imaginando esta situação, não é? (Afinal a menina é maior e tem mais massa…)
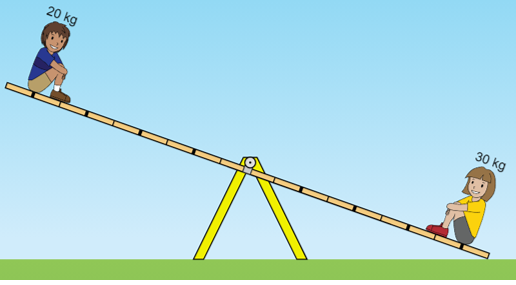Figura 1
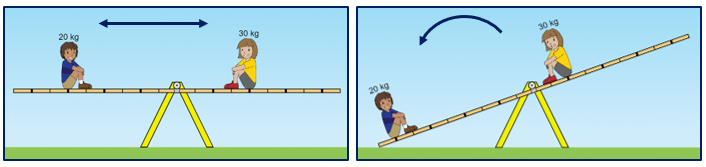
Mas as duas situações ilustradas a seguir também podem ocorrer…
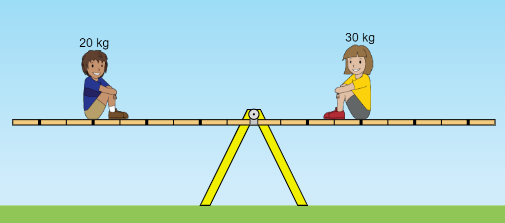Figura 2
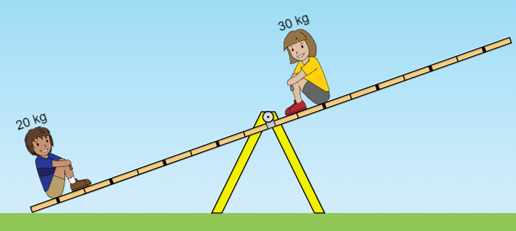Figura 3
Como justificá-las?
Bem, a Matemática e uma segunda discussão sobre Forças vão nos ajudar com isso…
Um pouquinho de Matemática e Física
Vamos retomar a discussão sobre a grandeza Força.
Na Sala 1, introduzimos informalmente o conceito Força, destacando a sua ação de causar deformações ou alterar o estado de repouso ou de movimento de um determinado objeto. Agora, vamos focar nosso estudo principalmente no movimento resultante da aplicação das forças potente e resistente em uma alavanca. Essas forças, até então, foram caracterizadas pelas respectivas direções e pelos respectivos sentidos de suas ações; mas apenas a direção e o sentido de uma força não serão suficientes para prosseguirmos com os nossos estudos!
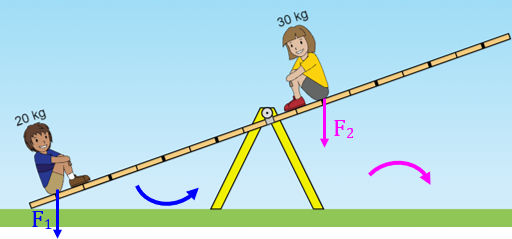
Perceba, por exemplo, que sabermos que temos duas forças, [tex]F_1[/tex] e [tex]F_2[/tex] atuando na direção vertical e de cima para baixo nos dois objetos que aparecem na gangorra mostrada na imagem a seguir não ajudaria entender porque a gangorra, inicialmente equilibrada horizontalmente, girou no sentido horário…
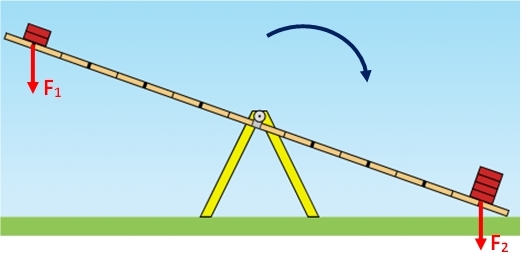Figura 4
Melhorando o entendimento sobre a grandeza Força
Não há uma definição precisa para o conceito de Força; de fato, o entendimento dessa grandeza é algo intuitivo. Nas várias situações em que uma força aparece, temos descrições do que ela faz, mas não o que ela é! De maneira simples, vamos continuar descrevendo que uma força é uma ação física que causa deformações ou que altera o estado de repouso/movimento de um determinado objeto.
Na discussão apresentada na Sala 1, exploramos apenas duas características do conceito de Força: a sua direção (horizontal, vertical, inclinada) e o seu sentido (da direita para à esquerda, da esquerda para direita, de cima para baixo, de baixo para cima, por exemplo). No entanto, uma força possui uma terceira característica: um número que usamos para indicar a sua intensidade e que recebe o nome de módulo.
Matematicamente, uma força é definida por um objeto matemático denominado vetor e, portanto, fica necessária e absolutamente definida por um número (módulo), uma direção e um sentido. (Por isso é que representamos vetores por segmentos orientados.)
Na Física, os vários tipos de força são grandezas vetoriais; assim, particularmente, as noções intuitivas de forças que discutiremos necessitam de um módulo, de um sentido e de uma direção para serem representadas e completamente definidas. E, por serem grandezas, devemos associar uma unidade de medida a cada tipo de força.
Assim, nesta Sala, além da utilização das unidades de medida, a novidade com relação às forças potente e resistente será a indicação dos respectivos módulos, ou seja, números que indicam suas intensidades.
Ao escrevermos uma grandeza vetorial, podemos colocar uma pequena setinha em cima da letra utilizada para denotá-la; por exemplo, podemos indicar a força potente por [tex]\vec{F_P}[/tex]. Nas nossas discussões, não utilizamos esta notação.
(Nesta Sala há uma breve discussão sobre a diferença entre grandezas escalares e vetoriais.)
Um exemplo importante de força para o estudo das alavancas é a denominada Força Gravitacional (ou Força Peso).
O valor do peso de um corpo qualquer na superfície terrestre depende apenas de sua massa e da gravidade terrestre. O peso [tex]P[/tex] e a massa [tex]m[/tex] de um objeto são relacionados pela identidade
[tex]\qquad \qquad P=m\cdot g\,[/tex],
na qual [tex]g[/tex] é a aceleração da gravidade de onde o objeto se encontra.
A aceleração da gravidade na Terra é de aproximadamente [tex]9,8\text{ m/s}^2[/tex]. Aqui nesta Sala, a menos que se afirme o contrário, utilizaremos a aproximação [tex]g\approx 10\text{ m/s}^2.[/tex]
Outras unidades de medida que utilizaremos:
para massas: quilograma-força ([tex]\text{kg}[/tex]);
para pesos: Newton ([tex]\text{N}[/tex]).
A igualdade [tex]\boxed{P=m\cdot g}[/tex] nos mostra que [tex]1\text{ N}[/tex] equivale a [tex]1 \text{ kg m/s}^2.[/tex]
Observe que essa igualdade também indica que o peso de cada um de nós varia de acordo com o valor da gravidade, diferentemente da nossa massa, que é a quantidade de matéria presente no nosso corpo e é a mesma em qualquer lugar. Até mesmo em outros planetas!
Imagem extraída do site Esquadrão do Conhecimento. (Acesso em 22/02/2024.)
Com esse reinício de discussão sobre Força, podemos observar que se conhecêssemos as massas dos objetos que aparecem sobre a alavanca da Figura 4 talvez pudéssemos entender o movimento de rotação da alavanca no sentido horário.
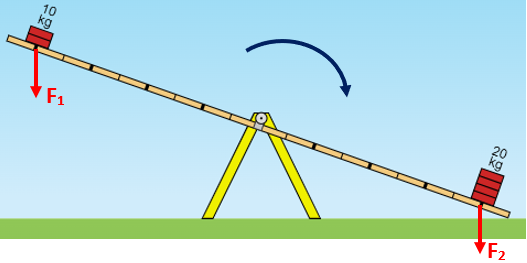Figura 5
A princípio poderíamos respirar aliviados, pois uma “força peso maior” explicaria o movimento da alavanca na Figura 5. Mas apenas essa justificativa não é necessariamente suficiente e nem correta; lembrem-se das situações ilustradas pelas Figuras 2 e 3…
Nas duas situações temos uma menina com mais massa, e consequentemente mais peso, do que o menino e as alavancas não fizeram um movimento de rotação no sentido horário:
● na Figura 2, a alavanca está em equilíbrio (posição horizontal);
● na Figura 3, a alavanca descreveu um giro no sentido anti-horário!
O movimento de uma alavanca
O vídeo a seguir, além de ilustrar boa parte das discussões que fizemos na Sala 1, vai nos dar uma pista para obtermos respostas sobre a Matemática escondida em uma alavanca e sobre o movimento de uma alavanca.
É só clicar na setinha e acompanhar atentamente toda a discussão.
No vídeo, é utilizado outro nome para o que chamamos de ponto fixo de uma alavanca na Sala 1: eixo de giro.
Alavancas – Ciências – Ens. Fund.
Vídeo do Canal Novo Telecurso
Vocês devem ter observado no vídeo que, se quisermos diminuir o nosso esforço ao usar uma alavanca, devemos colocar o ponto de apoio mais perto do objeto que desejamos mover.
Mas, por quê?
Antes de formalizar essa discussão, que tal tentarmos reproduzir a experiência que o Lineu propôs para a Maria no vídeo? A atividade evidenciará a importância do posicionamento do ponto de apoio para diminuir o esforço aplicado a uma alavanca interfixa.
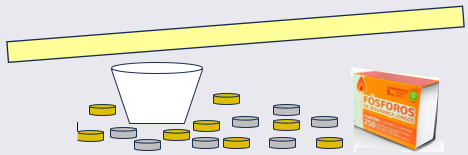
Material necessário:
● Várias moedas; ● 1 copo plástico; ● 1 caixa de fósforos cheia (caixa e encaixe). |
 |
Procedimentos:
1. Prenda o copo em uma das extremidades da régua. (Para deixar o copo bem firme, vocês podem fazer dois furinhos no fundo dele, passar por eles um pedaço de barbante e amarrar o copo na régua.)
2. Coloque as moedas dentro do copo. (Quanto mais moedas forem colocadas no copo, melhor será o efeito do experimento.)
3. Posicione a caixa de fósforos embaixo da régua, próxima à extremidade onde o copo está e segure-a com firmeza.
4. Uma segunda pessoa deve tentar levantar o copo, usando a extremidade livre da régua.
5. Agora, posicione a caixa de fósforo próxima ao meio da régua, segurando com firmeza.
6. A mesma pessoa que tentou levantar o copo deve repetir a experiência.
7. Para finalizar, posicione a caixa de fósforo bem próxima à extremidade livre da régua e segure-a firmemente.
8. Novamente, a pessoa que tentou levantar o copo anteriormente deve repetir a experiência.
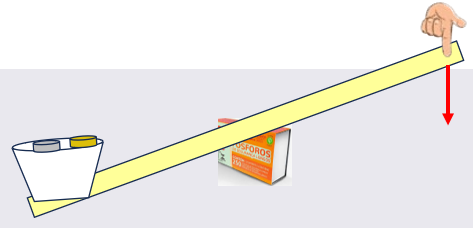
Repita o procedimento com outras pessoas levantando o copo, para que todos percebam que, quanto mais próximo o ponto de apoio (caixa de fósforos) estiver da carga (o copo, no nosso caso), menos força deverá ser feita para que essa carga seja levantada!
Com o “sobe e desce” da alavanca utilizada na Atividade 4, uma pergunta passa por nossas cabeças: fixando o ponto de apoio de uma alavanca em qualquer posição, é sempre possível equilibrá-la somente aplicando forças nas duas extremidades?
A próxima Atividade pode nos ajudar com a resposta.
Material necessário:
-
● 1 lápis
● fita adesiva
● 1 régua não flexível de 30 centímetros;
● moedas de R$ 0,10;
● 2 caixas de fósforo vazias (caixa e encaixe).
Ideia do experimento:
O experimento consiste em uma mini gangorra formada pela régua apoiada perpendicularmente sobre o lápis.
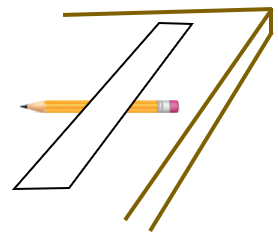
Quando equilibrada, a régua deve ficar parada horizontalmente em cima do lápis.
Procedimentos:
- Utilizando fita crepe, prenda o lápis pelas duas pontas sobre uma mesa, para que ele não rode.
- Apoie a régua perpendicularmente sobre o lápis e tente encontrar o ponto de equilíbrio do sistema “régua-lápis”, ou seja, a posição na qual a régua fique na horizontal. Anote o valor indicado na régua correspondente ao ponto de apoio (o lápis), em centímetros.
- Repita o procedimento, colocando em cada extremidade da régua uma caixa de fósforo vazia. Anote o valor indicado na régua correspondente ao ponto de apoio em que a régua pôde ser equilibrada.
- Coloque agora duas moedas de R$ 0,10 dentro de uma das caixas de fósforo e, na outra, apenas uma moeda de RS 0,10 e feche-as. As moedas devem ser idênticas. Com a régua em equilíbrio, coloque cuidadosamente uma caixa em cada extremidade da régua. A régua permaneceu equilibrada? O que aconteceu com ela?
- Com cuidado, tente equilibrar a régua e as caixas de fósforo com as moedas. Encontrada a nova posição de equilíbrio, anote o valor indicado na régua correspondente ao ponto de apoio, em centímetros.
- Retire as caixas de cima da régua.
- Com a régua equilibrada novamente, coloque dentro de cada uma das caixas duas moedas idênticas de R$ 0,10, feche a caixas e posicione cada caixa sobre a régua, a 10 centímetros do ponto de apoio. A régua permanece equilibrada? Faça o teste e justifique.
- Escreva uma breve conclusão sobre o que vocês observaram no experimento.
Com as Atividades 4 e 5 podemos perceber que forças aplicadas a uma alavanca podem fazer com que ela gire em torno do seu ponto fixo. Mas não apenas isso; essas atividades apontam para um elemento novo na definição do que acontece quando aplicamos uma força em uma alavanca: a distância entre o ponto fixo da alavanca e o ponto de aplicação da força. Essa distância foi o que definimos como braço de alavanca na Sala 1.
Mas como justificar que forças e distâncias se combinam para produzir ou evitar rotações?
É o que vamos tratar a seguir!
A rotação de uma alavanca
Geralmente, os corpos estão submetidos a mais de uma força.
Em algumas situações, as diversas forças que atuam sobre os corpos podem ser substituídas por uma força única, a resultante, cujo efeito de aplicação é o mesmo do conjunto de todas as forças inicialmente aplicadas simultaneamente.
Vejam, por exemplo, as duas situações ilustradas a seguir.
- ● Se cada rapaz que estiver empurrando o carro que aparece na imagem abaixo fizer uma força de direção horizontal e da esquerda para a direita, a força resultante será a força de intensidade igual à soma das intensidades das duas forças aplicadas pelo dois, com mesma direção e mesmo sentido. Se as intensidades das duas forças forem [tex]F_1[/tex] e [tex]F_2[/tex], então a intensidade da força resultante será [tex]F_1+F_2.[/tex]
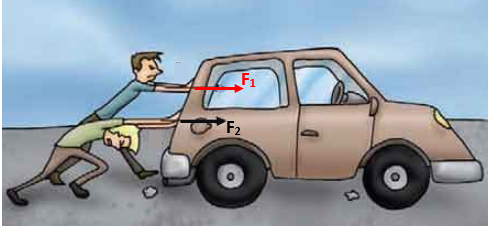Imagem adaptada do site REDU – Conteúdos Escolares. (Acesso em 22/02/2024.)
- ● Se o homem e o bode que aparecem na próxima imagem estiverem exercendo forças com mesma direção, mas com sentidos contrários, a resultante terá a direção e sentido da força de maior intensidade e o seu valor será a diferença entre a intensidade maior e a intensidade menor.
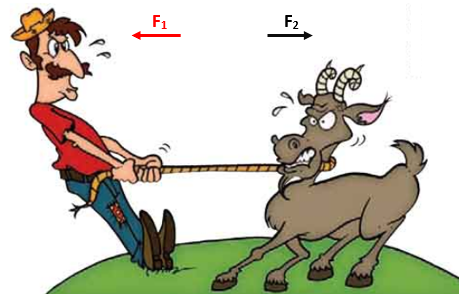Imagem adaptada do site REDU – Conteúdos Escolares. (Acesso em 22/02/2024.)
Essas duas situações ilustram o que chamamos de movimentos de translação provocado por uma ou mais forças. Mas quando falamos de alavancas, o movimento que mais interessa é o chamado movimento de rotação dessa alavanca em torno do seu ponto fixo, como temos afirmado nas nossas discussões. A própria denominação Ponto Fixo indica que não foram e não serão considerados movimentos de translação nas alavancas discutidas nas Salas 1 e 2. Dessa forma, nossas alavancas não sairão do lugar: no máximo, girarão! (Fisicamente, se uma alavanca está em repouso, isso significa que ela está em “equilíbrio estático” e “a resultante das forças nela aplicadas é zero”.)
E para analisar o efeito de uma ou mais forças agindo sobre um objeto para provocar rotação, entra em cena a grandeza física denominada Torque. Vamos conversar um pouco sobre essa nova grandeza; pois, se quisermos fazer com que um corpo gire em torno de algum ponto, devemos “produzir um torque sobre ele”.
Torque (ou momento de uma força) é uma grandeza física associada ao fato de uma força promover rotação, isto é, fazer com que o objeto (não necessariamente uma alavanca) no qual a força está aplicada gire em torno de um eixo.
Assim, resumidamente, o torque pode ser descrito como a “ação de girar de uma força [tex]F[/tex]”.
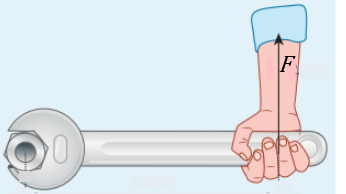Imagem adaptada do site BrainKart.(Acesso em 22/02/2024.)
IMPORTANTE: O Torque não é a força, mas sim a efetividade de uma força em causar rotação sobre um eixo específico.
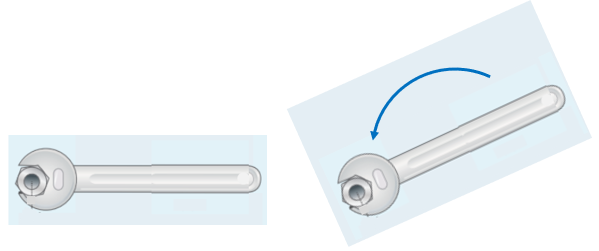
Essa grandeza pode ser calculada a partir da intensidade de uma força e da distância do seu ponto de aplicação no objeto ao eixo de rotação (ponto de giro).
Em particular, quando aplicamos uma força [tex]F[/tex] perpendicularmente à linha imaginária que liga o ponto de aplicação da força ao ponto de giro do objeto e desprezamos o peso desse objeto, o torque produzido [tex]T[/tex] pode ser facilmente calculado utilizando-se a expressão
[tex] \qquad \qquad T=f \cdot d[/tex],
na qual [tex]f[/tex] indica a intensidade da força [tex]F[/tex] (seu módulo) e [tex]d[/tex] indica a distância entre o ponto de giro e o ponto de aplicação da força [tex]F.[/tex]
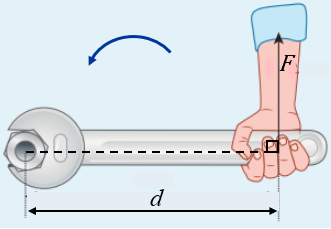Imagem adaptada do site BrainKart.(Acesso em 22/02/2024.)
Uma observação essencial, antes de prosseguirmos.
-
Para se calcular um torque, a igualdade [tex]\boxed{T=f \cdot d}[/tex] só deve ser utilizada quando a força [tex]F[/tex] que produzirá o torque for aplicada perpendicularmente à linha que liga o ponto de aplicação da força ao ponto de giro/rotação.
Essa fórmula, bastante utilizada com alavancas, é um caso particular da fórmula geral do torque [tex]T[/tex] resultante da aplicação de uma força [tex]F[/tex] a um objeto:
[tex] \qquad \qquad T=f \cdot d \cdot \text{sen }\theta[/tex],
na qual
[tex]\quad f[/tex] indica a intensidade da força [tex]F[/tex],
[tex]\quad d[/tex] indica a distância entre local de aplicação da força e o ponto de giro,
[tex]\quad \theta[/tex] é o ângulo entre o “segmento de reta que liga o ponto de giro ao ponto onde a força é aplicada” e o segmento orientado que representa a força [tex]F[/tex].
Vejamos em desenho:
Caso geral:
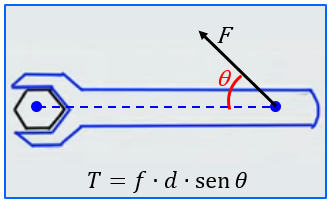
Caso particular:
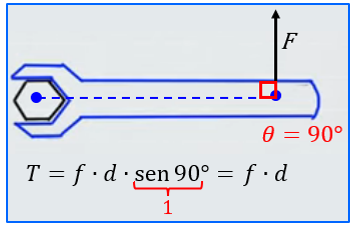
Se você ainda não aprendeu trigonometria, não se preocupe; utilizaremos nas nossas discussões sobre alavancas apenas a fórmula [tex] \boxed {T=f \cdot d}[/tex].
Observação: Quando não é utilizada a notação vetorial, é comum usar uma mesma notação para indicar tanto a força como a sua intensidade. Assim, é comum escrevermos a igualdade [tex]\boxed{T=f \cdot d}~[/tex] como [tex]~\boxed{T=F \cdot d}.[/tex]
Para finalizarmos essa breve apresentação sobre torque, é importante que se observe um detalhe dessa grandeza: o seu sinal. O torque tende produzir rotações e existem dois sentidos de rotação: o horário e o anti-horário. Assim, para distinguir um sentido do outro, convencionamos atribuir ao torque ou um sinal positivo ou um sinal negativo, dependendo do sentido de rotação que essa ação imprimirá a um objeto a partir do repouso:
● se o corpo girar no sentido anti-horário, o torque é positivo;
● se o corpo girar no sentido horário, o torque é negativo.
- ➤ Mas entenda, e lembre-se sempre, que o sinal negativo de um torque representa somente o sentido do giro que ele provoca e não uma intensidade negativa.
Por exemplo, a intensidade do torque [tex]\boxed{T_1=-50 \text{ N}\cdot \text{m}}[/tex] não é menor do que a intensidade do torque [tex]\boxed{T_2=5 \text{ N}\cdot \text{m}}[/tex], embora saibamos que [tex]-50 \lt 5[/tex]:
– o torque [tex]T_1[/tex] tem intensidade [tex]50 \text{ N}\cdot \text{m}[/tex] e imprimirá a um objeto, inicialmente parado, uma rotação no sentido horário,
– o torque [tex]T_2[/tex] tem intensidade [tex]5 \text{ N}\cdot \text{m}[/tex] e imprimirá a um objeto, inicialmente parado, uma rotação no sentido anti-horário,
ou seja, a intensidade do torque [tex]T_1[/tex] é maior do que a de [tex]T_2[/tex] e, com isso, a aplicação simultânea desses dois torques em um objeto provocará uma rotação no sentido horário (sentido da rotação provocada pelo torque de maior intensidade).
É devido a esse sinal de um torque que podemos somar os vários torques que podem atuar simultaneamente em um mesmo objeto e obter um torque resultante, ou total, que descreverá a ação conjunta de todos os torques aplicados. No exemplo acima teríamos um torque resultante [tex]T[/tex], assim definido:
[tex]\qquad T=T_1+T_2=-50+5=-45\text{ N}\cdot \text{m}[/tex],
isto é, um torque de intensidade [tex]45 \text{ N}\cdot \text{m}[/tex] que imprimirá ao objeto uma rotação no sentido horário, conforme já tínhamos previsto.
Agora, vamos nos concentrar nas alavancas!
Assumiremos que, nas nossas alavancas, todas as forças serão aplicadas perpendicularmente à linha imaginária que liga o ponto de giro ao ponto onde cada força é aplicada.
A igualdade [tex] \boxed{T=f \cdot d}[/tex] (ou [tex] \boxed{T=F \cdot d}[/tex]) nos garante que, quanto mais longe do eixo de rotação (ponto fixo) de uma alavanca uma força for aplicada, “maior será o giro que ela provocará”, conforme ilustra a figura a seguir.
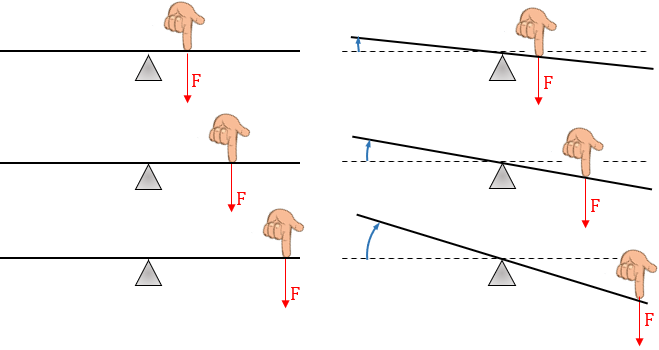
Assim, quanto mais distante do Ponto Fixo de uma alavanca uma força for aplicada, mais rotação ela produzirá (maior será o torque por ela produzido).
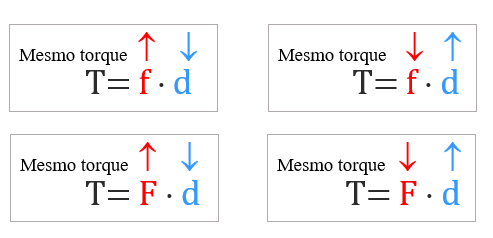
Particularmente, o fato verificado com a Atividade 4 é consequência direta das igualdades [tex] \boxed{T=f \cdot d}[/tex] e [tex] \boxed{T=F \cdot d}[/tex]: a intensidade de uma força aplicada a uma das extremidades de uma alavanca, com o intuito de mover um objeto na outra extremidade, é inversamente proporcional à “distância do ponto de aplicação dessa força” ao “ponto de apoio”.
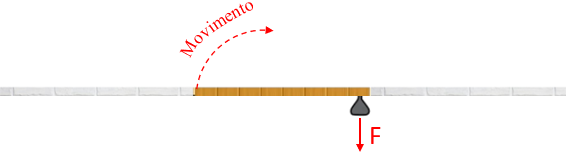
Quando fechamos uma porta, aplicamos uma força na maçaneta para ela rotacionar em torno de um eixo fixo onde estão as dobradiças.
Vocês já perceberam que a maçaneta de uma porta sempre está o mais longe possível das dobradiças, que definem o eixo de rotação da porta? Por quê?
Podemos responder esse porquê com a próxima atividade.
(1) Que tal você fazer a experiência de abrir ou fechar uma porta ou um portão da sua casa, fazendo força perpendicularmente à porta/portão e:
(i) bem perto da maçaneta?
(ii) no meio da porta ou portão?
(iii) bem perto das dobradiças?
O que você conclui com suas tentativas?
(2) Você já viu alguma porta cuja maçaneta fica no seu ponto central?
(3) Você já viu alguma porta cuja maçaneta fica do lado das dobradiças?
A partir da Atividade 6, podemos concluir que se as maçanetas das portas fossem fixadas próximas das dobradiças, que definem os eixos de rotação, a força feita para rotacionar uma porta para abri-la ou fechá-la seria muito grande. É por essa razão que as maçanetas são instaladas no ponto mais distante possível das dobradiças, demandando menor esforço para movimentar a porta. (Para um mesmo torque, maior distância implica em menor força.)
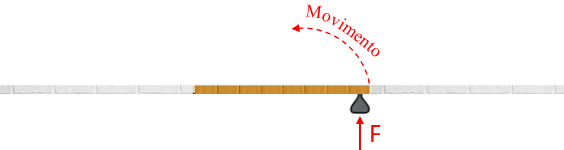
Que tal mais uma atividade?
(1) Tente resolver uma questão do ENEM 2013 que envolve chaves de roda e Binários de Forças.
Um Binário de Forças é a ação de duas forças de igual intensidade, mesma direção e sentidos opostos aplicadas em diferentes pontos de um objeto.
As figuras representam alguns modelos de chaves de roda:
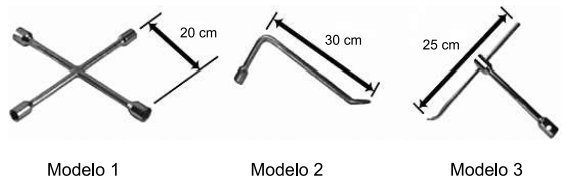
Em condições usuais, qual desses modelos permite a retirada da roda com mais facilidade?
a) 1, em função de o momento da força ser menor.
b) 1, em função da ação de um binário de forças.
c) 2, em função de o braço da força aplicada ser maior.
d) 3, em função de o braço da força aplicada poder variar.
e) 3, em função de o momento da força produzida ser maior.
Você pode conferir a sua solução, clicando no botão abaixo.
(2) Que tal uma pausa para diversão?
Então, assista a animação abaixo envolvendo chave de roda.
Vídeo – Momento de uma Força
A nossa próxima discussão será como utilizar o Torque para equilibrar uma alavanca. Mas antes, tentem resolver a atividade proposta no final da Sala 1.
Arquimedes “movendo o mundo”
Imagem extraída do site Science Photo Library. (Acesso em 22/02/2024.)
a. Mais longe do objeto que você deseja mover
b. Mais perto do objeto que você deseja mover
c. Você não move o fulcro (ponto de apoio), você move a força do esforço
d. Nenhuma das respostas anteriores
Agora ficou muito fácil, não é?
Equilíbrio de alavancas
Nesta discussão, continuaremos supondo que as forças aplicadas nas nossas alavancas não provocam translações; assim, o Ponto Fixo de cada uma delas não sairá do lugar e elas, no máximo, só giração em torno desse ponto.
Pode parecer um completo absurdo utilizar torque de uma força para equilibrar uma alavanca!
Afinal, o Torque, em última instância, não é a medida de quanto uma força que age em um objeto faz com que ele gire?
No entanto, é com essa grandeza que vamos contar. E já sabemos que, se uma força age perpendicularmente à linha imaginária que liga o ponto de giro ao ponto onde ela é aplicada, então:
- ● sempre que um torque produz uma rotação no sentido anti-horário, podemos utilizar a relação [tex]T=f \cdot d[/tex] (ou [tex]T=F \cdot d[/tex]) e
● sempre que um torque produz uma rotação no sentido horário, podemos utilizar a mesma relação acrescida de um sinal negativo.
Bem, o nosso foco agora é queremos alavancas em equilíbrio, ou seja, queremos alavancas paradinhas, sem se deslocarem e sem rodarem; e, de modo geral, temos duas condições para uma dada alavanca não se mover:
- ➤ A primeira, nós já incorporamos nas nossas discussões: a resultante das forças exercidas sobre ela deve ser nula.
➤ A segunda é a novidade: a soma dos torques das forças exercidas sobre ela também deve ser nula.
É essa segunda condição que vamos tentar entender.
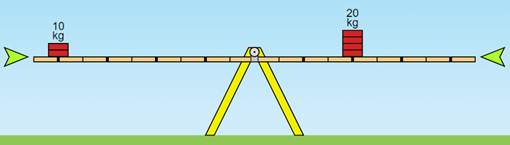
Ao colocar sobre a extremidade esquerda de uma gangorra, inicialmente na posição horizontal, um objeto de 10 Kg, ela vai descer para a esquerda.
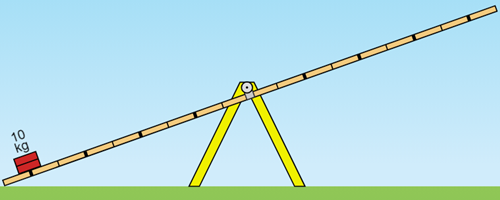
Agora, se, a partir dessa posição, colocarmos um objeto de 20 kg na outra extremidade, à mesma distância do ponto fixo (ponto de giro) da gangorra, o esperado é que a gangorra desça para a direita, como já observamos anteriormente.
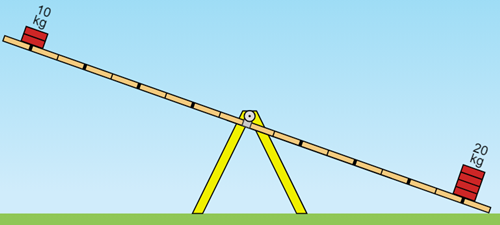
Mantendo o objeto de 10 kg na mesma posição, será que existe um local no qual possamos colocar o objeto de 20 kg, de forma que a gangorra fique equilibrada (na horizontal)?
A resposta é SIM, veja:
Justificativa:
Vamos focar na novidade: para uma alavanca estar em equilíbrio, a soma dos torques das forças exercidas sobre ela deve ser nula.
(1) Desprezando o peso da tábua da gangorra, nós temos duas forças atuando na gangorra, [tex]F_1[/tex] e [tex]F_2[/tex], ambas aplicadas perpendicularmente à tábua da gangorra.
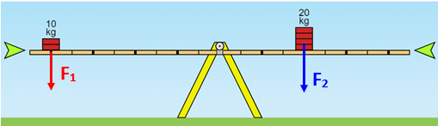
Vamos calcular as intensidades dessas duas “forças peso”:
[tex]\quad P_1=m_1 \cdot g=10 \cdot 10=100\text{ N}[/tex]
[tex]\quad P_2=m_2 \cdot g=20 \cdot 10=200\text{ N}[/tex].
(2) Para o cálculo da soma dos torques relativos a essas duas forças, é importante lembrar que:
● A força [tex]F_1[/tex] isoladamente produz uma rotação no sentido anti-horário, em torno do ponto fixo.
● A força [tex]F_2[/tex] isoladamente produz uma rotação no sentido horário, em torno do ponto fixo.
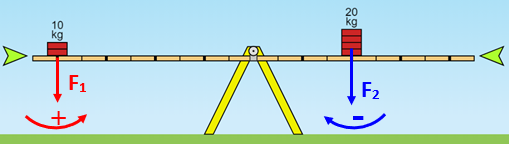
(3) Para o cálculo desses dois torques, precisaremos de dois braços de alavanca:
● [tex]b_1[/tex]: a distância entre o ponto de aplicação da força [tex]F_1[/tex] e o ponto fixo da nossa alavanca;
● [tex]b_2[/tex]: a distância entre o ponto de aplicação da força [tex]F_2[/tex] e o mesmo ponto fixo da nossa alavanca.
Observe a próxima figura.
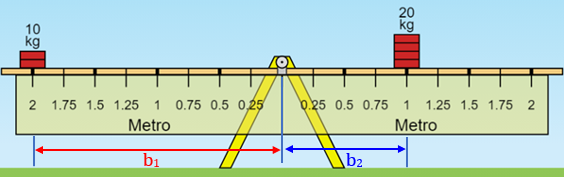
Pronto, já podemos calcular a soma dos torques [tex]T_1[/tex] e [tex]T_2[/tex], lembrando que a intensidade [tex]T[/tex] do torque produzido por uma força [tex]F[/tex] é dada por [tex] \boxed{T=f \cdot d}[/tex], sendo que [tex]f[/tex] indica a intensidade da força [tex]F[/tex] e [tex]d[/tex] indica a distância entre o ponto de giro e o ponto de aplicação da força [tex]F:[/tex]
[tex]\quad T_1+T_2=\left(P_1 \cdot b_1\right)-\left(P_2 \cdot b_2\right)\\
\quad T_1+T_2=100\cdot2-200 \cdot 1\\
\quad \fcolorbox{black}{#eee0e5}{$T_1+T_2=0$}~.[/tex]
Vamos analisar a situação com a qual abrimos as discussões desta Sala: um menino com 20 kg e uma menina com 30 Kg vão brincar em uma gangorra que inicialmente está na posição horizontal.
Se a menina sentar de um lado do brinquedo e o menino do outro lado, o que irá acontecer?
Bem, já conseguimos responder de modo geral a pergunta formulada: Depende da posição na qual eles vão sentar.
- (a) Vamos analisar, inicialmente, a situação da Figura 1. Para isso, vamos calcular os torques das forças, desprezando uma vez mais o peso da barra da gangorra.
Temos duas forças peso atuando, [tex]F_1[/tex] e [tex]F_2[/tex], ambas aplicadas perpendicularmente à tábua da gangorra.
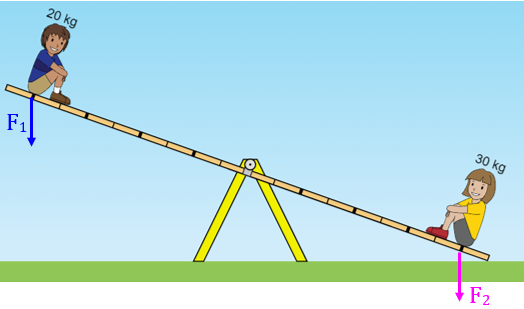
Calculemos as intensidades dessas forças:
[tex]\quad P_1=m_1 \cdot g=10 \cdot 20=200\text{ N}[/tex]
[tex]\quad P_2=m_2 \cdot g=10 \cdot 30=300\text{ N}[/tex].
Agora, observe que:
● isoladamente, a força [tex]F_1[/tex] produz uma rotação no sentido anti-horário.
● isoladamente, a força [tex]F_2[/tex] produz uma rotação no sentido horário,
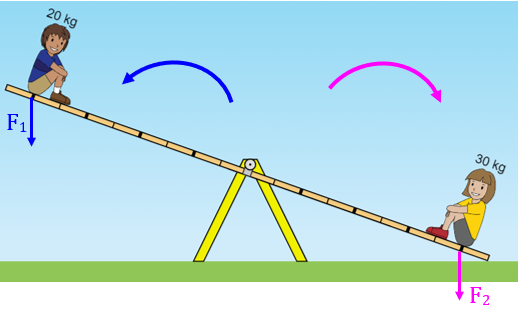
e os braços de alavanca são
● [tex]b_1=2 \text{ m}[/tex]
● [tex]b_2=2 \text{ m}.[/tex]
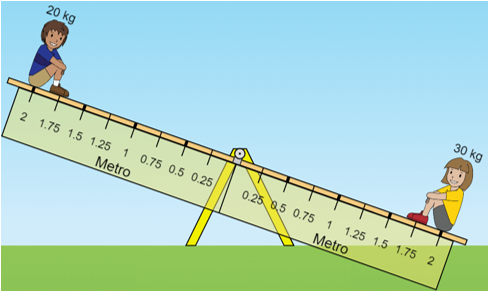
Assim, os torques relativos a essas duas forças são dados por:
[tex]\quad \color{#0000FF}{ T_1=+(200 \cdot 2)=400\text{ N}\cdot \text{m}} \\
\quad \color{#FF00FF}{ T_2=-(300 \cdot 2)=-600\text{ N}\cdot \text{m}}[/tex]
e, portanto,
[tex]\quad T_1+T_2=400-600
\quad \fcolorbox{black}{#eee0e5}{$T_1+T_2=-200 \lt 0$}.[/tex]
Como a soma dos torques que atuam na gangorra não é nula, essa gangorra não está em equilíbrio.
De fato, como a força [tex]F_2[/tex] exerceu um torque maior, a gangorra girou no sentido horário, ou seja, desceu para direita.
Numericamente podemos confirmar essa rotação observando que a soma dos torques deu negativa e isso caracteriza um torque resultante negativo, responsável por uma rotação final no sentido horário.
- (b) Vamos analisar agora a situação da Figura 2 e calcular os torques das forças, desprezando outra vez mais o peso da barra da gangorra.
Veremos que o equilíbrio, que a princípio nos pareceu absurdo, realmente ocorre.
As forças [tex]F_1[/tex] e [tex]F_2[/tex] estão aplicadas perpendicularmente à tábua da gangorra e as massas envolvidas são as mesmas, logo as intensidades das duas forças são as mesmas do item anterior, os respectivos pesos das duas crianças:
[tex]\quad P_1=200\text{ N}[/tex]
[tex]\quad P_2=300\text{ N}[/tex]
e os sentidos de rotação também.
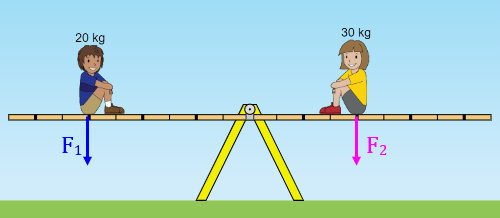
O que muda são os braços de alavanca e, consequentemente, as intensidades dos torques.
Os novos braços de alavanca são
● [tex]b_1=1,5 \text{ m}[/tex]
● [tex]b_2=1 \text{ m}[/tex]
e os novos torques passam a ser dados por:
[tex]\quad \color{#0000FF}{ T_1=200 \cdot 1,5=300\text{ N}\cdot \text{m}} \\
\quad \color{#FF00FF}{ T_2=-(300 \cdot 1)=-300\text{ N}\cdot \text{m}}.[/tex]
Assim, temos:
[tex]\quad T_1+T_2=300-300\\
\quad \fcolorbox{black}{#eee0e5}{$T_1+T_2= 0$}~[/tex]
e o equilíbrio não é apenas no desenho; em condições reais como as apresentadas, uma gangorra estará equilibrada.
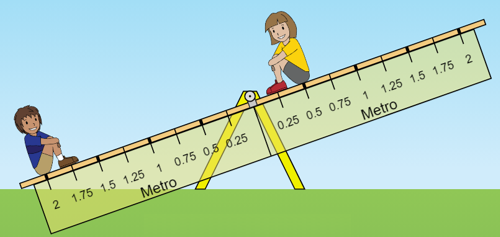
- (c) Das situações apresentadas no início das nossas discussões, a ilustrada pela Figura 3 era a que, intuitivamente, parecia a mais improvável de acontecer. Mas vamos ver que ela ocorre, mesmo!
Podemos observar que as forças [tex]F_1[/tex] e [tex]F_2[/tex] aplicadas são as mesmas dos itens anteriores; logo elas têm as mesmas intensidades e provocam os mesmos sentidos de rotação.
Mais uma vez, o que muda são os braços de alavanca e os torques:
● [tex]b_1=2 \text{ m}[/tex]
● [tex]b_2=0,5 \text{ m}[/tex]
[tex]\quad \color{#0000FF}{ T_1=200 \cdot 2=600\text{ N}\cdot \text{m}} \\
\quad \color{#FF00FF}{ T_2=-(300 \cdot 0,5)=-150\text{ N}\cdot \text{m}}.[/tex]
Assim, temos:
[tex]\quad T_1+T_2=600-150\\
\quad \fcolorbox{black}{#eee0e5}{$T_1+T_2= 450\text{ N}\cdot \text{m}$}~[/tex]
e a gangorra descendo para a esquerda também não é apenas no desenho: em condições como as apresentadas, isso ocorrerá.
Podemos generalizar as duas situações de equilíbrio da gangorra apresentadas acima; vejamos como.
Princípio fundamental das alavancas
Vamos analisar a situação de equilíbrio de uma alavanca (a princípio interfixa), com peso desprezível, na qual atuam uma força potente e uma força resistente, perpendicularmente à barra da alavanca. (Perceba que se as duas forças provocarem rotações no mesmo sentido, a alavanca não estará em equilíbrio.)
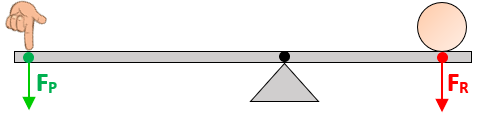
Rigorosamente, nesta figura faltou especificar uma terceira força: a força normal [tex]N[/tex], devido ao contato da barra da alavanca com o ponto fixo.
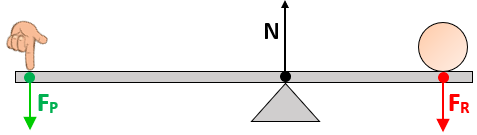
Supondo que as forças aplicadas não provocam translações, devemos calcular os torques gerados por essas três forças e impor que a soma deles seja nula. Observe que, em particular, o torque [tex]T_N[/tex] gerado pela força [tex]N[/tex]é dado por [tex]T_N=N\cdot d[/tex], sendo que [tex]d[/tex] é a distância entre o ponto de aplicação da força [tex]N[/tex] e o ponto fixo. Como [tex]d=0[/tex], [tex]T_N=0[/tex] e, assim, não há necessidade prática de consideramos a força normal devido ao contato da barra da alavanca com o ponto fixo quando analisamos a soma de torques neste caso e em qualquer outro que envolva alavancas. Devido a isso é que não incluímos a força normal nos exemplos que fizemos sobre rotações de alavancas.
Considerando, então, apenas as forças potente e resistente, vamos calcular a soma dos torques gerados por elas e impor que essa soma seja zero.
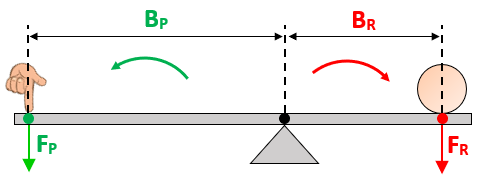
Se [tex]T_P[/tex] e [tex]T_R[/tex] são os torques produzidos, respectivamente pelas forças potente e resistente, temos que:
[tex]\quad T_P=\left(F_P \cdot B_P\right)\\
\quad T_R=-\left(F_R \cdot B_R\right)[/tex]
então,
[tex]\quad T_P+T_R=F_P \cdot B_P-F_R \cdot B_R.[/tex]
Como para o equilíbrio devemos ter [tex]T_P+T_R=0[/tex], segue que
[tex]\quad T_P+T_R=0\\
\quad F_P \cdot B_P-F_R \cdot B_R=0\\
\quad F_P \cdot B_P=F_R \cdot B_R. [/tex]
Portanto, na condição de equilíbrio, devemos ter [tex]\boxed{F_P \cdot B_P=F_R \cdot B_R}[/tex]; assim, todas as vezes que uma alavanca estiver em equilíbrio teremos uma igualdade entre os momentos das forças resistente e potente.
Note que utilizamos uma alavanca interfixa para ilustrar os cálculos efetuados para obtenção do equilíbrio; no entanto, a mesma lei vale para outros tipos de alavancas. (Que tal você tentar justificar essa afirmação?)
Assim, pra efeito de registro geral, na condição de equilíbrio de uma alavanca de qualquer tipo cujas forças potente e resistente produzam torques com sentidos contrários, devemos ter:
[tex]\quad F_R\cdot d_R=F_P\cdot d_P[/tex],
sendo [tex]F_R[/tex] e [tex]F_P[/tex] as intensidades da força resistente e da força potente, respectivamente, enquanto que [tex]d_R[/tex] e [tex]d_P[/tex] são, respectivamente, a distância da aplicação dessas forças ao ponto de apoio da alavanca.
A igualdade [tex]\boxed{F_R\cdot d_R=F_P\cdot d_P}[/tex] é conhecida como Princípio fundamental das alavancas ou Equação fundamental das alavancas.
Que tal um vídeo no qual podemos ver uma aplicação da Equação fundamental das alavancas em uma alavanca inter-resistente, além de rever itens discutidos nas Salas 1 e 2?
É só clicar botão abaixo e Bom Proveito!
Vamos ver um exemplo?
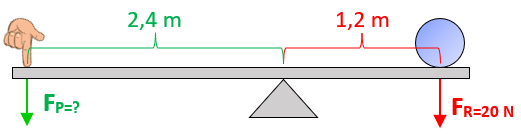
Solução:
Nesse exemplo, queremos descobrir a intensidade da força potente, que é aplicada a [tex]2,4 \text{ m}[/tex] do ponto de apoio. Sabemos, observando a figura, que a força resistente é de [tex]20 \text{ N}[/tex], e está aplicada a [tex]1,2 \text{ m}[/tex] do ponto de apoio.
Na condição de equilíbrio, devemos ter [tex]F_R\cdot d_R=F_P\cdot d_P[/tex].
Substituindo os valores conhecidos, ficamos com:
[tex]\quad 20\cdot1,2=F_P\cdot2,4[/tex]
[tex]\quad 24=F_P\cdot2,4[/tex]
[tex]\quad F_P=24\div2,4=10\text{ N}.[/tex]
Assim, para que essa alavanca fique em equilíbrio, a força potente deve ser igual a [tex]10\text{ N}.[/tex] Isso também indica que, para erguer o objeto, é necessária e suficiente uma força maior do que [tex]10\text{ N}.[/tex]
Agora, que tal mais um vídeo para ilustrar boa parte do que discutimos?
Máquinas Simples – alavanca
Neste vídeo, relações entre forças e distâncias em uma alavanca são apresentadas olhando as rotações da alavanca de um modo diferente: simplesmente como distâncias percorridas por suas extremidades.
Para finalizarmos esta Sala, não poderíamos sonegar uma informação matemática: Torque é uma grandeza vetorial.
Mas isso é assunto para outra ocasião…
Por agora, vamos praticar?
É só clicar no botão abaixo e ir para a Sala 3.
B O N S E S T U D O S ! ! !
Se necessário, na Sala 3 você encontrará um link para voltar para esta Sala ou para a Sala 1, na parte inferior à direita da página.
Equipe COM – OBMEP