Clique no botão abaixo para visualizar o problema.
Problema
(Indicado a partir do 2º ano do E. M.)
(UPE, 2013 – Adaptado) Oito amigos entraram em um restaurante para jantar e sentaram-se em torno de uma mesa retangular, com oito lugares, como mostra a figura a seguir:
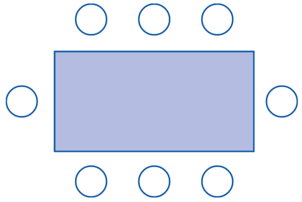
Dentre todas as configurações possíveis, quantas são as possibilidades de dois desses amigos, Ana e Beto, ficarem sentados em frente um do outro?

Lembrete
✏ Princípio Fundamental da Contagem, ou Princípio Multiplicativo, para dois eventos:
Se
- um evento E1 puder ocorrer de [tex] m_1 [/tex] maneiras,
- e um evento E2 puder ocorrer de [tex]m_2 [/tex] maneiras,
e esses dois eventos forem independentes entre si (isto é, a ocorrência de um não muda a quantidade de possibilidades para a ocorrência do outro), então a quantidade de maneiras em que os dois eventos ocorrem ao mesmo tempo é
[tex]\qquad \qquad \boxed{m_1\times m_2} \,.[/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
Solução
- Ana pode sentar em qualquer uma das oito cadeiras disponíveis. Definida a cadeira em que Ana irá sentar, automaticamente estará definida a cadeira de Beto, já que eles devem ficar um em frente do outro. Assim, existem [tex]8[/tex] maneiras distintas de Ana e Beto se acomodarem.
- Para cada umas dessas [tex]8[/tex] maneiras, existem ainda [tex]6![/tex] modos de os demais amigos sentarem juntos à mesa.
Logo, pelo Princípio Fundamental da Contagem, o total de possibilidades de Ana e Beto ficarem sentados em frente um do outro é [tex]8\times 6! =5760[/tex].
Solução elaborada pelos Moderadores do Blog.
