Clique no botão abaixo para visualizar a Sala.
O matemático francês Édouard Lucas (1842-1891), criador do famoso jogo Torre de Hanói, formulou um problema desafiador pouco antes de sua morte, em 1891.
 Édouard Lucas
Édouard Lucas
Imagem extraída de Mancala World.
O problema possui o seguinte enunciado:
“De quantas maneiras [tex]n[/tex] casais ([tex]n \geq 3[/tex]) podem sentar em [tex]2n[/tex] cadeiras diferentes em torno de um círculo de modo que pessoas do mesmo sexo não se sentem juntas e que nenhum homem fique ao lado de sua respectiva mulher?”
O enunciado do problema é bem simples, não é mesmo? Já a sua solução…
Esse problema ficou conhecido como o Problema de Lucas, ou Ménage Pròbleme, e os matemáticos da época demoraram mais de meio século para resolvê-lo.
Particularmente, em 1943, o matemático canadense-americano Irving Kaplansky (1917-2006) apresentou uma solução para o Problema de Lucas em um artigo publicado no Bulletin of the American Mathematical Society. Nessa solução, Kaplansky desenvolveu dois métodos de contagem que são conhecidos hoje como “Lemas de Kaplansky”. (Na Matemática, lema é um resultado intermediário que é utilizado para provar um outro resultado mais importante.)
 Irving Kaplansky
Irving Kaplansky
Imagem extraída de PeoplePill.
A solução do Problema de Lucas não é o nosso foco principal; os Lemas de Kaplansky são os objetos de estudo desta Sala!
Enunciaremos esses resultados e resolveremos alguns problemas de contagem com essas novas ferramentas. Apesar de não serem comumente abordados nas escolas durante o estudo da Análise Combinatória, veremos que as aplicações desses lemas são simples e nos ajudarão a solucionar exercícios bem interessantes. Com relação ao Problema de Lucas, devido à variedade de técnicas de contagem em sua resolução, deixaremos sua demonstração no final da Sala apenas como leitura para os interessados.
Alguns conceitos e princípios de contagem serão necessários para uma boa compreensão do tema: Combinação simples; Princípio Multiplicativo e Princípio Aditivo. Se você não se lembra deles é só clicar no botão abaixo.
✏ Combinação simples: Uma das maneiras de agruparmos elementos de um dado conjunto é escolhê-los levando-se em consideração apenas a sua natureza, sem se importar em que ordem eles foram escolhidos ou apresentados. Esse tipo de agrupamento de elementos é denominado uma Combinação simples. Particularmente, quando escolhemos [tex]r[/tex] dentre [tex]n[/tex] elementos de um conjunto dessa forma, dizemos que estamos definindo uma Combinação simples de [tex]n[/tex] elementos tomados [tex]r[/tex] a [tex]r[/tex]. A quantidade desse tipo de agrupamentos é denotada por [tex]C_{n,r}[/tex] ou [tex]C_n^r\,[/tex] e assim definida:
[tex]C_{n,r}=C_n^r=\dfrac{n!}{(n-r)!\,r!} \text{, com } n,r\in\mathbb{N} \text{ e } r\leqslant n[/tex].
✏ Princípio Fundamental da Contagem, ou Princípio Multiplicativo: Se
- uma decisão D1 puder ser tomada de [tex] m_1 [/tex] maneiras distintas,
- uma decisão D2 puder ser tomada de [tex] m_2 [/tex] maneiras distintas,
- [tex]\cdots[/tex]
- uma decisão Dk puder ser tomada de [tex]m_k [/tex] maneiras distintas e
- todas essas decisões forem independentes entre si (isto é, a escolha de uma não muda a quantidade de possibilidades para a escolha de outra),
então o número total de maneiras de tomarmos sucessivamente essas [tex]k[/tex] decisões (D1 e D2 e [tex]\cdots[/tex] e Dk) é igual ao produto
[tex]\qquad \qquad \boxed{m_1\times m_2 \times \cdots \times m_k} \, .[/tex]
✏ Princípio Aditivo: Se
- uma decisão D1 puder ser tomada de [tex] m_1 [/tex] maneiras distintas,
- uma decisão D2 puder ser tomada de [tex] m_2 [/tex] maneiras distintas,
- [tex]\cdots[/tex]
- uma decisão Dk puder ser tomada de [tex]m_k [/tex] maneiras distintas e
- todas essas decisões forem independentes entre si (isto é, a escolha de uma não muda a quantidade de possibilidades para a escolha de outra),
então, a quantidade de maneiras de tomarmos uma das [tex]k[/tex] decisões (D1 ou D2 ou [tex]\cdots[/tex] ou Dk) é
[tex]\qquad \qquad \boxed{m_1+ m_2 + \cdots + m_k} \, .[/tex]
Para compreendermos a utilidade do Primeiro Lema de Kaplansky, vamos começar explorando a resolução de um problema, antes de apresentarmos o Lema.
[tex]\qquad \qquad A = \{1, 2, 3, 4, 5, 6, 7, 8\},[/tex]
de modo que em cada subconjunto não haja números consecutivos?
Solução:
Para que não haja a necessidade de enumerar exaustivamente todos os subconjuntos com a propriedade requerida, ao definir um subconjunto de [tex]A[/tex], iremos marcar com o sinal [tex]+[/tex] a posição dos elementos que farão parte do subconjunto e com o sinal [tex]−[/tex] a posição dos elementos que não farão parte, considerando a posição dos elementos na sequência [tex] 1, 2, 3, 4, 5, 6, 7, 8.[/tex] Assim, por exemplo:
[tex]\qquad \{3, 6, 8\}[/tex] seria representado por [tex]\,-\,-\,+\, \,-\,-\,\,+\,-\,+[/tex],
[tex]\qquad \{4, 5, 7\}[/tex] seria representado por [tex]\, -\,-\,-\,+\,+\,-\,+\,-[/tex].
Observe que, particularmente, o conjunto do primeiro exemplo representa uma possibilidade de escolha para este problema, mas o do segundo não, já que [tex]4[/tex] e [tex]5[/tex] são consecutivos.
Para formar um subconjunto com três elementos, sem dois números consecutivos, devemos distribuir três sinais [tex]+[/tex] e cinco sinais [tex]−~[/tex], sem que haja dois sinais [tex]+[/tex] consecutivos.
Para fazer isso:
● colocamos os cinco sinais [tex]−[/tex] (o primeiro passo da escolha);
●em seguida, distribuímos os três sinais [tex]+[/tex] nos seis espaços que ficaram definidos (representados abaixo pelos quadradinhos), com no máximo um sinal por espaço. Perceba que isso pode ser feito de [tex]C_{6}^{3}[/tex] maneiras diferentes.![]()
Finalmente, utilizando o princípio Multiplicativo, temos [tex]\boxed{1 \cdot C_{6}^{3}=20}[/tex] subconjuntos.
No caso geral, o número de subconjuntos com [tex]p[/tex] elementos de [tex]\{1,2,3,…,n\}[/tex], com [tex]p\leq n/2[/tex], nos quais não há números consecutivos é [tex]C_{n-p+1}^{p}[/tex].
Justificativa: Seguindo o mesmo raciocínio da resolução do Problema 1, devemos ter [tex]p[/tex] sinais [tex]+[/tex] e “[tex]n-p[/tex]” sinais [tex]-[/tex]. Ao distribuir os sinais [tex]-~[/tex], temos “[tex]n-p+1[/tex]” espaços para os [tex]p[/tex] sinais [tex]+[/tex]. Assim, teremos:
● [tex]1[/tex] modo de posicionar os sinais [tex]–[/tex] e
● [tex]C_{n-p+1}^{p}[/tex] maneiras de organizar os sinais [tex]+[/tex] nos espaços criados.
Assim, não haverá números consecutivos nos subconjuntos.
Este é exatamente o Primeiro Lema de Kaplansky:
O número de subconjuntos com [tex]p[/tex] elementos de [tex]\{1,2,3,…,n\}[/tex], sendo [tex]p\leq n/2 [/tex] e nos quais não há números consecutivos, é:
[tex]\qquad \qquad \boxed{f(n,p)= C_{n-p+1}^{p}}.[/tex]
Mesmo sabendo de sua importância, o objetivo principal desta Sala não é a notação em si, mas sim resolver problemas de contagem utilizando essa nova técnica. Na verdade, a ideia central é repetir esse raciocínio, mas em problemas com “roupagens” diferentes.
Então, que tal resolver alguns problemas?
Quantas são as possibilidades distintas de se atender às condições dessa reposição?
Solução:
Vamos representar cada um dos nove sábados disponíveis para reposição, em sequência, por um elemento do conjunto
[tex]\qquad \qquad S=\{1,2,3,4,5 ,6,7,8,9\}[/tex].
Assim, para resolver este problema, vamos procurar subconjuntos do conjunto [tex]S[/tex] com quatro elementos que não sejam números consecutivos, já que as reposições não devem ser feitas em sábados consecutivos.
Para formar um subconjunto com quatro elementos, sem dois números consecutivos, devemos distribuir quatro sinais [tex]+[/tex] e cinco sinais [tex]−[/tex], sem que haja dois [tex]+[/tex] consecutivos.
Assim,
● distribuímos os cinco sinais [tex]−[/tex] (o primeiro passo da escolha)
● em seguida, nos seis espaços que ficaram definidos, colocamos os quatro sinais [tex]+[/tex], com no máximo um sinal por espaço. ![]() Perceba que isso pode ser feito de [tex]C_{6}^{4}=15[/tex] maneiras diferentes.
Perceba que isso pode ser feito de [tex]C_{6}^{4}=15[/tex] maneiras diferentes.
Em notação, teremos: [tex]f(9,4)= C_{9-4+1}^{4}=C_{6}^{4}[/tex].
Logo, pelo Princípio Multiplicativo, a escola tem [tex]\boxed{1\cdot C_{6}^{4}=1 \cdot 15=15}[/tex] maneiras diferentes de repor essas aulas.
Solução:
Vamos representar cada um dos quatorze dias possíveis por um elemento do conjunto
[tex]\qquad \qquad M=\{1,2,3,4,5,6,7,8,9,10,11,12,13,14\}.[/tex]
Assim, devemos contar quantos subconjuntos de [tex]S[/tex] com [tex]5[/tex] elementos existem de modo a não ter elementos consecutivos. Para realizar essa contagem,
● colocamos os nove sinais [tex]−[/tex];
● em seguida, distribuímos os cinco sinais [tex]+[/tex] nos dez espaços que ficaram definidos.
![]()
Perceba que isso pode ser feito de [tex]C_{10}^{5}=252[/tex] maneiras diferentes.
Usando a notação definida, teremos [tex]f(14,5)= C_{14-5+1}^{5}=C_{10}^{5}=252[/tex].
Esse número representa as maneiras de escolher os dias das provas. Mas, após escolher os dias, temos que organizar a ordem na qual as provas serão aplicadas e isso pode ser feito de [tex]5!=120[/tex] modos.
Portanto, pelo Princípio Multiplicativo, há [tex]\boxed{252\cdot 120=30240}[/tex] modos de aplicar essas provas.
Note que, até aqui, todos os problemas apresentavam, basicamente, sempre a mesma restrição: apenas não possuir números consecutivos.
E se, por exemplo, quiséssemos contar quantos subconjuntos, com [tex]3[/tex] elementos, do conjunto [tex]S=\{1,2,3,4,5,6,7,8,9,10\}[/tex] podemos formar de modo que entre dois elementos escolhidos para o subconjunto haja pelo menos [tex]2[/tex] elementos não escolhidos, como por exemplo o subconjunto [tex]\{2,6,9\}[/tex]?
Vamos lá!
Novamente, iremos marcar com o sinal [tex]+[/tex] a posição dos elementos que farão parte do subconjunto e com o sinal [tex]−[/tex] a posição dos elementos que não farão parte. Assim:
[tex]\qquad \{2, 6, 9\}[/tex] seria representado por [tex]\,-\, +\, -\, -\, -\, +\, -\, -\, +\, -\,,[/tex]
[tex]\qquad \{3, 5, 10\}[/tex] seria representado por [tex]\,- \,- \,+ \,- \,+ \,- \,- \,- \,- \,+\,.[/tex]
(Observe que, particularmente, o conjunto do primeiro exemplo representa uma possibilidade de escolha, mas o do segundo não, já que [tex]3[/tex] e [tex]5[/tex] não possuem dois elementos não escolhidos entre eles.)
Para fazer essa contagem, vamos, inicialmente, posicionar os [tex]3[/tex] sinais de [tex]+[/tex] formando uma fila e deixando [tex]4[/tex] espaços entre eles.![]() Os sinais de [tex]–[/tex] serão colocados nesses espaços. Vamos chamar de [tex]x,\,y,\, z[/tex] e [tex]w[/tex] a quantidade de sinais [tex]–[/tex] que colocaremos no primeiro, segundo, terceiro e quarto espaços, respectivamente.
Os sinais de [tex]–[/tex] serão colocados nesses espaços. Vamos chamar de [tex]x,\,y,\, z[/tex] e [tex]w[/tex] a quantidade de sinais [tex]–[/tex] que colocaremos no primeiro, segundo, terceiro e quarto espaços, respectivamente.![]() Dessa forma, devemos ter a seguinte equação linear com soluções inteiras e não negativas:
Dessa forma, devemos ter a seguinte equação linear com soluções inteiras e não negativas:
[tex]\qquad x+y+z+w=7[/tex], com [tex]y \geq 2~[/tex] e [tex]~z \geq 2.[/tex]
Na Sala de Estudos sobre Combinações Completas aprendemos a contar quantas soluções tem uma equação desse tipo, com esse tipo de restrições.
Substituindo, [tex]y=a+2[/tex] e [tex]z=b+2[/tex], obtemos a equação [tex]x+a+b+w=3[/tex], que tem
[tex]\qquad CR_{4}^{3}=C_{4+3-1}^{3}=C_{6}^{3}= \dfrac {6!}{3! \cdot 3!}= 20[/tex] soluções.
Portanto, há [tex]20[/tex] subconjuntos com [tex]3[/tex] elementos de modo que entre dois elementos escolhidos para o subconjunto haja pelo menos [tex]2[/tex] elementos não escolhidos.
É dessa forma que iremos generalizar o Primeiro Lema de Kaplansky.
Seguindo o mesmo raciocínio, vamos indicar pelo sinal [tex]+[/tex] os elementos selecionados e pelo sinal [tex]-[/tex] os não selecionados. Assim, arrumamos uma fila com [tex]p[/tex] sinais [tex]+[/tex] e [tex](n-p)[/tex] sinais [tex]-[/tex] de modo que entre dois sinais [tex]+[/tex] haja pelo menos [tex]r[/tex] sinais [tex]-[/tex].
Chamando de [tex]x_{1},\,x_{2},\,x_{3},\, \dots ,\,x_{p}[/tex] e [tex]x_{p+1}[/tex] a quantidade de sinais [tex]–[/tex] que serão colocados em cada um dos [tex]p+1[/tex] espaços existentes entre os sinais [tex]+[/tex], temos que
[tex]\qquad x_{1}+x_{2}+x_{3}+ \dots +x_{p}+x_{p+1}=n-p[/tex], com [tex]x_{1},~x_{p+1} \geq 0~[/tex] e [tex]~x_{2},~x_{3},~\dots~,~x_{p} \geq r[/tex].
![]()
Como buscamos apenas soluções inteiras não negativas, podemos resolver a equação fazendo as seguintes substituições
[tex]\qquad \boxed{x_{2}=r+y_{2}}[/tex], [tex]~\boxed{x_{3}=r+y_{3}}, ~\dots~ ,\, \boxed{x_{p}=r+y_{p}}[/tex]
na equação
[tex]\qquad x_{1}+x_{2}+x_{3}+ \dots +x_{p}+x_{p+1}=n-p.[/tex]
Com isso, segue que:
[tex]\qquad x_{1}+(r+y_{2})+(r+y_{3})+ \dots + (r +y_{p})+x_{p+1}=n-p\\
\qquad x_1+y_2+y_3+⋯+y_p+x_{p+1}+(p-1)r=n-p\\
\qquad x_{1}+y_{2}+y_{3}+ \dots + y_{p} +x_{p+1}=n-p-(p-1)r.[/tex]
Como todas as incógnitas são números inteiros não negativos, aprendemos na Sala Combinação Completa que essa equação possui [tex]\boxed{CR\,_{p+1}^{n-p-(p-1)r}=C_{n-(p-1)r}^{p}= \dfrac {[n-(p-1)r]!}{p! \cdot [n-p-(p-1)r]!}}[/tex] soluções.
Assim, já podemos apresentar a generalização prometida do Primeiro Lema de Kaplansky:
Dado um conjunto [tex]\{1,2,3,4,…,n \}[/tex], o número de subconjuntos com [tex]p[/tex] elementos de modo que entre cada dois elementos escolhidos para o subconjunto haja pelo menos [tex]r[/tex] elementos não escolhidos é:
[tex]\qquad \qquad \boxed{f(n,p,r)=C_{n-(p-1)r}^{p}}.[/tex]
Observe que:
Para [tex]r=0[/tex], temos [tex]f(n,p,0)= C_{n}^{p}[/tex]; o que corresponde ao número de Combinações Simples de [tex]n[/tex] elementos tomados [tex]p[/tex] a [tex]p.[/tex]
Para [tex]r=1[/tex], temos [tex]f(n,p,1)=C_{n-p+1}^{p}[/tex]; o que corresponde ao Primeiro Lema de Kaplansky.
O Segundo Lema de Kaplansky apresenta a mesma ideia do Primeiro Lema; porém, impõe uma consideração extra de que [tex]1[/tex] e [tex]n[/tex] são números consecutivos.
Portanto, consideraremos nesta discussão que os números [tex]1,~2,~3,~…,~n [/tex] estão colocados em círculo, nesta ordem.
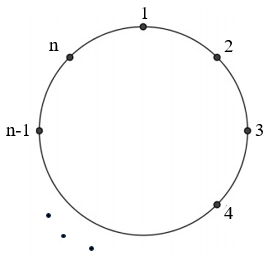
Por estarem em círculo, os números [tex]1[/tex] e [tex]n[/tex] agora são consecutivos. Para resolver este problema, vamos determinar:
(I) a “quantidade de subconjuntos que satisfazem as condições do problema e aos quais o elemento [tex]1[/tex] pertence” e
(II) a “quantidade de subconjuntos que satisfazem as condições do problema e aos quais o elemento [tex]1[/tex] não pertence”.
(I) Se o elemento [tex]1[/tex] pertence ao subconjunto, então devemos escolher [tex](p-1)[/tex] elementos do conjunto [tex]\{3,4,5,…,n-1\}[/tex] (como o [tex]1[/tex] figura no conjunto, não podemos ter os elementos [tex]2[/tex] e [tex]n[/tex]) tomando o cuidado de não escolhermos elementos consecutivos.
Ora, como vimos no Primeiro Lema de Kaplansky, o número de maneiras de escolhermos [tex](p-1)[/tex] elementos (sinais [tex]+[/tex]) em um conjunto que possui [tex](n-3)[/tex] elementos (portanto, [tex](n-3)-(p-1)[/tex] sinais [tex]-[/tex]) sem que haja elementos consecutivos é dado por:
[tex]\qquad \qquad f(n-3,p-1)=C_{n-3-(p-1)+1}^{p-1}=C_{n-p-1}^{p-1}\,.\qquad \textcolor{#8B5A2B}{(i)}[/tex]
(II) Se o elemento [tex]1[/tex] não pertence ao subconjunto, então devemos escolher [tex]p[/tex] elementos do conjunto [tex]\{2,3,4,…,n\}[/tex] (como o [tex]1[/tex] não figura no conjunto, podemos ter os elementos [tex]2[/tex] e [tex]n[/tex]) tomando o cuidado de não escolhermos elementos consecutivos.
Novamente, pelo Primeiro Lema de Kaplansky, o número de maneiras de escolhermos [tex]p[/tex] elementos (sinais [tex]+[/tex]) em um conjunto que possui [tex](n-1)[/tex] elementos (portanto, [tex](n-1-p)[/tex] sinais [tex]-[/tex]) sem que haja elementos consecutivos é dado por:
[tex]\qquad \qquad f(n-1,p)=C_{n-1-p+1}^{p}=C_{n-p}^{p}\,.\qquad \textcolor{#8B5A2B}{(ii)}[/tex]
Pelo Princípio Aditivo, por [tex]\textcolor{#8B5A2B}{(i)}[/tex] e por [tex]\textcolor{#8B5A2B}{(ii)}[/tex], a quantidade [tex]Q[/tex] de subconjuntos em questão é dada por:
[tex]\qquad Q=C_{n-p-1}^{p-1}~+~C_{n-p}^{p}~.[/tex]
Utilizando agora a definição de combinação simples, temos:
[tex]\qquad Q=C_{n-p-1}^{p-1}~+~C_{n-p}^{p}\\
\qquad Q=\dfrac {(n-p-1)!}{(p-1)!\cdot (n-2p)!} + \dfrac{(n-p)!}{p! \cdot (n-2p)!}\\
\qquad Q=\dfrac{(n-p-1)! \cdot p+(n-p)!}{p! \cdot (n-2p)!}\\
\qquad Q=\dfrac {(n-p-1)! \cdot[p+(n-p)]}{p! \cdot (n-2p)!}\\
\qquad Q=\dfrac {n \cdot (n-p-1)!}{p! \cdot (n-2p)!}\\
\qquad Q= \dfrac {n}{(n-p)} \cdot \dfrac{(n-p)!}{p! \cdot (n-2p)!}\\
\qquad Q= \dfrac {n}{(n-p)} \cdot C_{n-p}^{p}\,.[/tex]
Assim, podemos apresentar o Segundo Lema de Kaplansky:
O número de subconjuntos com [tex]p[/tex] elementos do conjunto [tex]\{1,2,3,…,n \}[/tex] nos quais não há números consecutivos, considerando [tex]1[/tex] e [tex]n[/tex] como consecutivos, é igual a
[tex]\qquad \qquad \boxed{g(n,p)=\dfrac {n}{n-p} \cdot C_{n-p}^{p}}.[/tex]
Não estamos interessados que você apenas utilize e memorize as fórmulas apresentadas; mas que, principalmente, você pratique e entenda as técnicas de contagem. Assim, note que ao resolvermos um problema com o Segundo Lema, utilizamos duas vezes o Primeiro Lema e o Princípio Aditivo.
Vejamos mais dois problemas…
Solução:
Vamos representar cada um dos sete dias da semana (segunda, terça, quarta, quinta, sexta, sábado e domingo) por um elemento do conjunto [tex]S=\{1,2,3,4,5 ,6,7 \}[/tex]. Perceba que no nosso problema os números [tex]1[/tex] e [tex]7[/tex] são consecutivos.
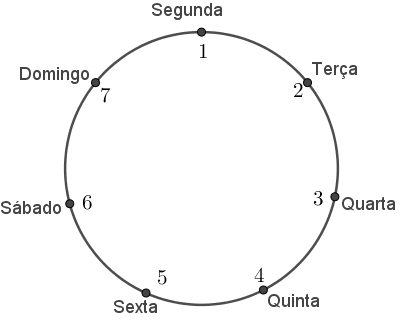
Então, vamos abrir o problema em dois casos:
(I) O dia [tex]1[/tex] foi escolhido; e
(II) O dia [tex]1[/tex] não foi escolhido.
- (I) No primeiro caso, com o [tex]1[/tex] no conjunto, temos apenas três situações a considerar: [tex]\{1,3,5 \}[/tex], [tex]\{1,3,6 \}[/tex] e [tex]\{1,4,6 \}[/tex]. Poderíamos ter conseguido esse resultado sem a necessidade de escrever todas as soluções:
Utilizando o Primeiro Lema de Kaplansky, como o [tex]1[/tex] já foi escolhido, temos que escolher dois elementos do conjunto [tex]\{3, 4, 5, 6 \}[/tex] sem que haja dois consecutivos. Daí, temos dois sinais [tex]–[/tex] e dois sinais [tex]+[/tex]:
[tex]\qquad \qquad \quad \quad\textcolor{#4B240B}{ \Box~-~\Box~-~\Box} [/tex]
Ao formar uma fila com os sinais [tex]-[/tex], há [tex]C_{3}^{2}=3[/tex] modos de posicionar os sinais [tex]+[/tex].
(II) Já no segundo caso, temos que escolher três elementos [tex]\{ 2,3,4,5,6,7 \}[/tex] sem que haja números consecutivos. Aqui devemos ter três sinais [tex]–[/tex] e três sinais [tex]+[/tex], sem que haja dois sinais [tex]+[/tex] consecutivos.
[tex]\qquad \qquad \quad \quad\textcolor{#4B240B}{ \Box~-~\Box~-~\Box~-~\Box} [/tex]
Ao formar uma fila com os sinais [tex]-[/tex], há [tex]C_{4}^{3}=4[/tex] modos de posicionar os sinais [tex]+[/tex].
Logo, pelo Princípio Aditivo, há [tex]\boxed{3+4=7}[/tex] maneiras para a escolha dos dias de aula.
Observe que, utilizando a fórmula do Segundo Lema de Kaplansky, temos:
[tex]\qquad \qquad g(7,3)= \dfrac{7}{7-3} \cdot C_{7-3}^{3}= \dfrac{7}{4} \cdot 4=\boxed{~7~}.[/tex]
Solução:
(1) O número de maneiras de escolhermos as [tex]4[/tex] cadeiras das [tex]15[/tex] possíveis em círculo, sem que haja cadeiras adjacentes, pode ser calculada pelo Segundo Lema de Kaplansky:
[tex]\quad \begin{align}g(15,4)&=\dfrac{15}{15-4} \cdot C_{15-4}^{4}= \dfrac{15}{11} \cdot C_{11}^{4}\\
&= \dfrac {15}{11} \cdot \dfrac {11!}{4! \cdot (11-4)!}\\
&=450.\end{align}[/tex]
Portanto, existem [tex]450[/tex] modos de escolher as cadeiras que serão ocupadas.
(2) Após escolher as cadeiras, devemos posicionar os amigos; o que pode ser feito de [tex]4!=24[/tex] maneiras.
Finalizando, pelo Princípio Multiplicativo há [tex]\boxed{450 \cdot 24=10800}[/tex] soluções para o problema.
Podemos generalizar o Segundo Lema, assim como fizemos para o Primeiro.
Para ajudar na generalização, considere o problema a seguir e acompanhe atentamente a sua solução.
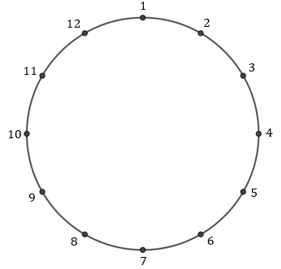
Solução:
Observe que o que queremos calcular é a quantidade de subconjuntos, com [tex]3[/tex] elementos, do conjunto
[tex]\qquad \qquad \quad \quad S= \{1,2,3,4,5,6,7,8,9,10,11,12 \}[/tex], sendo [tex]1[/tex] e [tex]12[/tex] consecutivos,
de modo que entre dois elementos escolhidos para o subconjunto haja pelo menos [tex]2[/tex] elementos não escolhidos; como, por exemplo, os subconjuntos [tex]\{1,4,10 \}[/tex], [tex]\{2,7,11 \}[/tex] e [tex]\{3,6,12 \}[/tex].
Para resolver este problema, vamos dividi-lo em dois casos:
1º) Os subconjuntos que contêm algum dos elementos [tex]\{ 1, 2 \}[/tex]; e
2º) Os subconjuntos que não contêm nenhum dos elementos [tex]\{ 1, 2 \}[/tex].
- 1º) Para a contagem do primeiro caso, como o [tex]1[/tex] já figura no conjunto, não podemos ter os elementos [tex]2[/tex], [tex]3[/tex], [tex]11[/tex] e [tex]12[/tex]. Assim, devemos escolher dois elementos do conjunto [tex]\{4,5,6,7,8,9,10 \}[/tex] de modo que haja pelo menos duas cadeiras vazias entre os escolhidos.
● Ora, como vimos na generalização do Primeiro Lema de Kaplansky, o número de maneiras de escolhermos dois elementos em um conjunto que possui sete elementos de modo que não haja pelo menos dois elementos consecutivos é dado por:
[tex]\qquad f(7,2,2)=C_{7-(2-1)2}^{2}=C_{5}^{2}=10.[/tex]
● De modo análogo, também temos [tex]10[/tex] subconjuntos, satisfazendo a restrição, em que o elemento [tex]2[/tex] está contido.
Assim, temos [tex]2 \cdot 10=20[/tex] subconjuntos que contêm algum dos elementos do conjunto [tex]\{1, 2 \}[/tex].
2º) Para a contagem do segundo caso, como os elementos [tex]1[/tex] e [tex]2[/tex] não pertencem ao subconjunto, então devemos escolher três cadeiras do conjunto [tex]\{ 3,4,5,6,7,8,9,10,11,12 \}[/tex] de modo que haja pelo menos duas cadeiras vazias entre os escolhidos.
Novamente, pela generalização do Primeiro Lema de Kaplansky, o número de maneiras de escolhermos [tex]3[/tex] elementos em um conjunto que possui [tex]10[/tex] elementos de modo que entre cada dois elementos escolhidos haja, no conjunto, pelo menos [tex]2[/tex] não escolhidos é:
[tex]\qquad f(10,3,2)=C_{10-(3-1) \cdot 2}^{3}=C_{6}^{3}=20.[/tex]
Portanto, pelo Princípio Aditivo, a solução deste problema é dada pela soma das quantidades encontradas nos casos, ou seja, [tex]20 + 20 = \boxed{40 \text{ subconjuntos}}.[/tex]
Assim, já podemos generalizar o Segundo Lema de Kaplansky. Essa generalização é a resposta à seguinte pergunta:
Essa quantidade de subconjuntos pode ser calculada pela soma do “número de subconjuntos satisfazem as exigências e não contêm um dos elementos [tex]\{1,2,3,4, \cdots , r \}[/tex]” com “o número de subconjuntos que satisfazem as exigências e contêm um desses elementos”.
Então, vamos calcular essa soma.
Observe que:
O número de subconjuntos que satisfazem as exigências e não contêm um dos elementos [tex]\{1,2,3,4, \cdots , r \}[/tex] é igual a [tex]f(n-r,p,r).[/tex]
O número de subconjuntos que satisfazem as exigências e contêm um desses elementos é igual a [tex]r \cdot f(n-2r-1,p-1,r).[/tex]
Calculando a soma [tex]S=f(n-r,p,r)+rf(n-2r-1,p-1,r)[/tex], temos:
[tex]\qquad S=C_{n-r-(p-1) \cdot r}^{p} + r\cdot C_{n-2r-1-(p-1-1) \cdot r}^{p-1}\\
\qquad S=C_{n-p \cdot r}^{p} + r \cdot C_{n-p \cdot r-1}^{p-1}\\
\qquad S=C_{n-p \cdot r}^{p}+r \cdot \dfrac {(n-p \cdot r-1)!}{(p-1)! \cdot (n-p \cdot r-p)!}\\
\qquad S=C_{n- p \cdot r}^{p}+ r \cdot \dfrac {(n-p \cdot r-1)!}{(p-1)!\cdot (n-p \cdot r-p)!} \cdot \dfrac {(n-p \cdot r)}{(n-p \cdot r)} \cdot \dfrac {p}{p}\\
\qquad S=C_{n-p \cdot r}^{p}+ \dfrac {p \cdot r} {n-p \cdot r} \cdot C_{n-p\cdot r}^{p}\\
\qquad S=C_{n-p \cdot r}^{p} \cdot \left(1+ \dfrac {p \cdot r}{n-p \cdot r}\right)\\
\qquad S=\dfrac {n} {n-p \cdot r} \cdot C_{n-p \cdot r}^{p}\,.[/tex]
A notação dessa generalização é [tex]\boxed{g(n,p,r)= \dfrac {n} {n-p \cdot r} \cdot C_{n-p \cdot r}^{p}}.[/tex]
Aqui está a generalização prometida do Segundo Lema de Kaplansky:
O número de subconjuntos com [tex]p[/tex] elementos do conjunto [tex]\{1,2,3,4, \cdots , n \}[/tex], considerando [tex]1[/tex] e [tex]n[/tex] consecutivos, de modo que entre cada dois elementos escolhidos para o subconjunto haja pelo menos [tex]r[/tex] elementos não escolhidos é dado por:
[tex]\qquad \qquad \boxed{g(n,p,r)= \dfrac {n} {n-p \cdot r} \cdot C_{n-p \cdot r}^{p}}.[/tex]
Note que:
Para [tex]r=0[/tex], temos [tex]g(n,p,0)= C_{n}^{p}[/tex]; o que corresponde ao número de Combinações Simples de [tex]n[/tex] elementos tomados [tex]p[/tex] a [tex]p.[/tex]
Para [tex]r=1[/tex], temos [tex]g(n,p,1)= \dfrac {n} {n-p} \cdot C_{n-p}^{p}[/tex]; o que corresponde ao Segundo Lema de Kaplansky.
Que tal você resolver alguns exercícios?
Basta imaginar o conjunto [tex]\{1, 2, 3, 4, …, 14, 15 \}[/tex], onde os elementos escolhidos recebem o sinal [tex](+)[/tex] e os elementos não escolhidos [tex](-)[/tex].
Portanto, teremos [tex]10[/tex] sinais [tex]-[/tex] gerando [tex]11[/tex] espaços.
Agora, temos [tex]C_{11}^{5}= 462[/tex] maneiras para distribuir os sinais [tex]+[/tex].
Portanto, o professor tem [tex]462[/tex] modos de escolher as cadeiras.
Para que as letras S não fiquem lado a lado, basta escolher [tex]4[/tex] espaços não adjacentes dois a dois.
Pelo Primeiro Lema de Kaplansky, isso pode ser feito de [tex]f(10,4)=C_{7}^{4}=35[/tex] maneiras.
Após escolhidas as posições das letras S, temos que arrumar as outras letras ([tex]4[/tex] letras I, [tex]1[/tex] letra M e [tex]1[/tex] letra P) nos [tex]6[/tex] espaços restantes, o que pode ser feito por uma permutação com repetição [tex]P_{6}^{4,1,1}= \dfrac {6!}{4!\,1!\,1!}=30[/tex].
Pelo Princípio Multiplicativo, há [tex]35 \cdot 30=1050[/tex] anagramas.
A expressão que representa a quantidade de maneiras distintas das três agentes serem distribuídas nos vagões é
a) [tex]C_{4}^{3}+3![/tex]
b) [tex]C_{6}^{3}[/tex]
c) [tex]C_{4}^{3} \cdot 3![/tex]
d) [tex]P_{6}^{3}[/tex]
e) [tex]P_{4}^{3} \cdot 3![/tex]
1º) Escolher os três vagões que as agentes serão distribuídas;
2º) Organizar as três agentes nesses vagões.
A primeira decisão possui [tex]f(6,3)=C_{4}^{3}[/tex] e a segunda decisão possui [tex]P_{3}=3![/tex] possibilidades de escolha.
Logo, pelo Princípio Multiplicativo, temos [tex]C_{4}^{3} \cdot 3![/tex] maneiras distintas.

a) [tex]72[/tex]
b) [tex]108[/tex]
c) [tex]144[/tex]
d) [tex]192[/tex]
e) [tex]216[/tex]
Isso pode ser feito de [tex]f(6,3)=C_{4}^{3}=4[/tex] maneiras.
Porém, como a ordem de ocupação desses lugares resulta em soluções diferentes, temos [tex]P_{3}=3!=6[/tex] possibilidades de acomodação para essas [tex]4[/tex] maneiras.
Logo, há [tex]4 \cdot 6=24[/tex] possibilidades para as três primeiras ocupações.
E para as três ocupações seguintes temos, também, [tex]P_{3}=3!=6[/tex] possibilidades de escolha.
Pelo Princípio Multiplicativo, há [tex]24 \cdot 6=144[/tex] soluções.
Entretanto, existe também a possibilidade de iniciar a ocupação com as cadeiras [tex]2[/tex] e [tex]5[/tex]. Isso pode ocorrer de [tex]P_{2}=2!=2[/tex] modos. Logo em seguida, temos [tex]P_{4}=4!=24[/tex] modos para as quatro ocupações seguintes.
Novamente pelo Princípio Multiplicativo, há [tex]2 \cdot 24=48[/tex] soluções.
Assim, pelo princípio aditivo, há [tex]144+48=192[/tex] maneiras de ocupação.
Imagine os doze cavaleiros em um círculo.
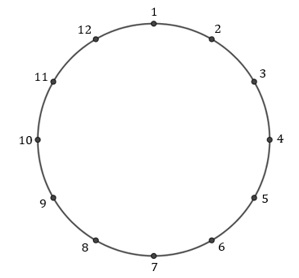
Devemos escolher cinco sem que haja cavaleiros consecutivos.
1º caso: Se o cavaleiro [tex]1[/tex] pertence ao grupo, então devemos escolher [tex]4[/tex] cavaleiros do conjunto [tex]\{3,4,5, \cdots , 11 \}[/tex] (como o [tex]1[/tex] já figura no conjunto, não podemos ter os cavaleiros [tex]2[/tex] e [tex]12[/tex]) tomando o cuidado de não pegarmos cavaleiros consecutivos. Isso pode ser feito de [tex]f(9,4)=C_{6}^{4}=15[/tex] maneiras.
2º caso: Se o cavaleiro [tex]1[/tex] não pertence ao grupo, então devemos escolher [tex]5[/tex] cavaleiros do conjunto [tex]\{2,3,4,5,6,7,8,9,10,11,12 \}[/tex] de modo que não haja cavaleiros consecutivos. Isso pode ser feito de [tex]f(11,5)=C_{7}^{5}=21[/tex] maneiras.
Portanto, há [tex]15+21=36[/tex] soluções.
Utilizando a notação do Segundo Lema de Kaplansky, [tex]g(12,5)=\dfrac {12}{(12-5)} \cdot C_{(12-5)}^{5}= \dfrac {12}{7} \cdot C_{7}^{5}=36[/tex] soluções.
 Imagem adaptada do site iStock. (Acesso em 24/01/2024.)
Imagem adaptada do site iStock. (Acesso em 24/01/2024.)
Além disso, temos [tex]P_{4}=4!=24[/tex] maneiras de arrumação dos carros nessas vagas.
Assim, pelo Princípio Multiplicativo, existem [tex]294 \cdot 24=7056[/tex] maneiras de ocupar as quatro vagas.
Obs: Na solução desse exercício não consideramos a possibilidade de rotação do estacionamento.
Pelo Segundo Lema de Kaplansky, há [tex]g(12,4)=\dfrac {12}{8} \cdot C_{8}^{4}[/tex] possibilidades para a escolha dos assentos dos homens. Além disso, temos [tex]P_4=4![/tex] e [tex]P_8=8![/tex] maneiras de acomodar os homens e as mulheres, respectivamente. Como a mesa pode ser girada de [tex]12[/tex] maneiras, contamos cada solução [tex]12[/tex] vezes.
Assim, a resposta do problema é [tex]\dfrac {\dfrac {12}{8} \cdot C_{8}^{4} \cdot 4! \cdot 8!}{12}=203\;212\;800[/tex].
Para encerrar, caso queira ver a Solução de Kaplansky para o Problema de Lucas, clique AQUI.
A versão apresentada foi extraída da referência [3] e pode trazer alguma dificuldade para quem não está habituado com a leitura de textos de Matemática.
Equipe COM – OBMEP
[1] A Matemática do Ensino Médio (volume 2): Coleção do Professor de Matemática – Elon Lages Lima; Paulo Cesar Pinto Carvalho; Eduardo Wagner e Augusto César Morgado.
[2] A Matemática do Ensino Médio (volume 2): Coleção do Professor de Matemática – Elon Lages Lima; Paulo Cesar Pinto Carvalho; Eduardo Wagner e Augusto César Morgado.
[3] Análise Combinatória e Probabilidade – Augusto César Morgado; João Bosco Pitombeira de Carvalho; Paulo Cesar Pinto Carvalho e Pedro Fernandez.
[4] Matemática Discreta: Coleção Profmat – Augusto César Morgado; Paulo Cesar Pinto Carvalho.
[5] O Problema de Lucas (Ménage Pròbleme) – Francisco Carpegiani Medeiros Borges. Online Encyclopedia Riordanica
