✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 9º ano do E. F.)
O grande astrônomo alemão Johannes Kepler (1571–1630) era um admirador da beleza do triângulo retângulo com o menor cateto medindo uma unidade de comprimento e as medidas dos três lados formando uma progressão geométrica.
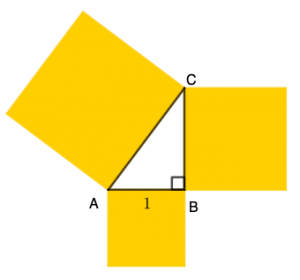
(a) Calcule a razão da progressão geométrica formada pelas medidas dos lados desse triângulo. Calcule também as áreas dos quadrados formados com os lados do triângulo de Kepler.
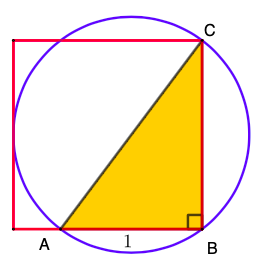
(b) Kepler observou que um círculo de diâmetro igual ao da hipotenusa do seu triângulo tem perímetro muito próximo, com erro inferior a [tex]0,1\%[/tex], ao do quadrado com lado igual à medida do maior cateto. Isso leva a uma aproximação para o valor de [tex]\pi[/tex], encontre-a.
Solução
(a) Se denotarmos por [tex]r[/tex] a razão da progressão geométrica, então os lados do triângulo de Kepler medirão [tex]1[/tex], [tex]r[/tex] e [tex]r^2[/tex].
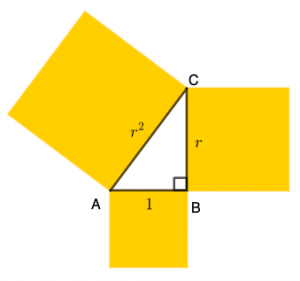
Como se trata de um triângulo retângulo, podemos aplicar o Teorema de Pitágoras obtendo a igualdade [tex]1^2+r^2=(r^2)^2.[/tex]
Com a substituição [tex]r^2=x[/tex], obtemos a equação do segundo grau [tex]x^2-x-1=0, [/tex] cujas soluções são [tex]x_1=\dfrac{1+\sqrt{5}}{2}, \ \ \ x_2=\dfrac{1-\sqrt{5}}{2}.[/tex]
Como o menor cateto mede [tex]1[/tex], segue que a razão [tex]r[/tex] da progressão geométrica deve ser um número positivo maior do que [tex]1[/tex], o mesmo sendo válido para [tex]x=r^2[/tex].
Assim, a única solução válida é [tex]x=\boxed{\dfrac{1+\sqrt{5}}{2}}.[/tex]
Esse número é conhecido como número de ouro e simbolizado por [tex]\phi[/tex] (para saber mais sobre o número de ouro, visite esta Sala.)
Logo, [tex]r=\pm \sqrt{\phi}[/tex]; mas, como [tex]r[/tex] é positivo, finalmente encontramos a única solução para o nosso problema: [tex]\boxed{r=\sqrt{\phi}}.[/tex]
Observe que as áreas dos três quadrados formados sobre os lados do triângulos são [tex]1[/tex], [tex]\phi[/tex] e [tex]\phi^2[/tex].
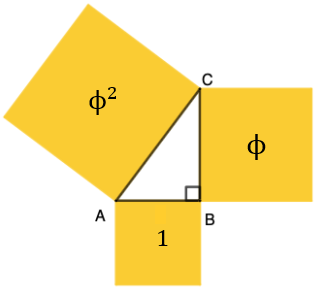
O triângulo de Kepler combina dois conceitos matemáticos fundamentais: o Teorema de Pitágoras e a Proporção Áurea, que impressionaram Kepler profundamente, como ele mesmo expressou:
– A geometria tem dois grandes tesouros, um é o teorema de Pitágoras; o outro, a divisão de um segmento em média e extrema razão. O primeiro pode ser comparado a uma medida de ouro; o segundo podemos chamar de joia preciosa.
(b) Agora que conhecemos as medidas dos lados do triângulo de Kepler, podemos calcular os perímetros do quadrado e do círculo em questão.
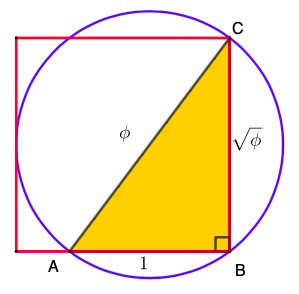
Perímetro do círculo:
[tex]\qquad P_c=2\pi r\\
\qquad P_c=2\pi \dfrac{\phi}{2}\\
\qquad \boxed{P_c=\pi\phi}.[/tex]
Perímetro do quadrado:
[tex]\qquad P_q=4l\\
\qquad \boxed{P_q=4\,\sqrt{\phi}}.[/tex]
Finalizando, como esses dois perímetros são próximos e [tex]\phi=\dfrac{1+\sqrt{5}}{2}\approx 1,618[/tex], segue que:
[tex]\qquad \pi\phi\approx4\sqrt{\phi}\\
\qquad \pi \approx \dfrac{4\sqrt{\phi}}{\phi} \\
\qquad \pi\approx \dfrac{4}{\sqrt{\phi}} \\
\qquad \pi\approx \dfrac{4}{\sqrt{1,618}} \\
\qquad \pi\approx \dfrac{4}{1,272} \\
\qquad \boxed{\pi\approx 3,1447}.[/tex]
Solução elaborada pelos Moderadores do Blog.
