Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F. – Nível de dificuldade: Médio)
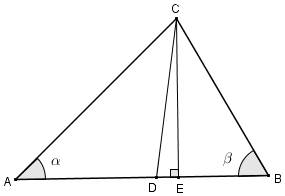
No triângulo [tex]ABC[/tex] da figura, as medidas em graus dos ângulos [tex]B\hat{A}C[/tex] e [tex]A\hat{B}C[/tex] são [tex]\alpha[/tex] e [tex]\beta[/tex], respectivamente.
Sabendo que [tex]\overline{CD}[/tex] é a bissetriz do ângulo [tex]A\hat{C}B[/tex] e [tex]\overline{CE}[/tex] é perpendicular a [tex]\overline{AB}[/tex], qual a medida em graus do ângulo [tex]D\hat{C}E[/tex]?
(A)[tex] \, \dfrac{180-(\alpha-\beta)}{2}[/tex]
(B)[tex] \, \dfrac{\beta-\alpha}{2}[/tex]
(C)[tex] \, \dfrac{\alpha+2\beta}{2}[/tex]
(D)[tex] \, \dfrac{360-\alpha-2\beta}{2}[/tex]
(E)[tex] \, \dfrac{\alpha+\beta}{2}[/tex]

Lembretes
✐ Bissetriz de um triângulo é um segmento com extremidades em um vértice desse triângulo e no respectivo lado oposto e que divide o ângulo interno definido por esse vértice em dois ângulos com a mesma medida.
✐ A soma das medidas dos ângulos internos de um triângulo é [tex]180^{\circ}[/tex]. (Se precisar, visite esta página.)
Solução
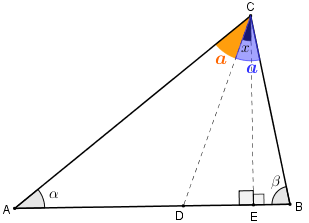
Como [tex]\overline{CD}[/tex] é a bissetriz do ângulo [tex]A\hat{C}B[/tex], então os ângulos [tex]A\hat{C}D[/tex] e [tex]D\hat{C}B[/tex] têm a mesma medida. Seja [tex]a[/tex] a medida em graus desses ângulos, conforme mostra a figura ao lado. Nessa figura, indicamos por [tex]x[/tex] a medida em graus do ângulo [tex]D\hat{C}E[/tex] e a qual iremos calcular.
- Observe, inicialmente, que a soma das medidas dos ângulos internos do triângulo [tex]ACB[/tex] é [tex]180^{\circ}[/tex]; assim:
[tex]\qquad \alpha+2a+\beta=180^{\circ}. \qquad \textcolor{#800000}{(i)}[/tex] - Também, a soma das medidas dos ângulos internos do triângulo [tex]ECB[/tex] é [tex]180^{\circ}[/tex], portanto:
[tex]\qquad 90^{\circ}+(a-x)+\beta=180^{\circ}[/tex]
[tex]\qquad a=x-\beta+90^{\circ}. \qquad \textcolor{#800000}{(ii)}[/tex]
Por [tex]\textcolor{#800000}{(i)} \, [/tex] e [tex] \, \textcolor{#800000}{(ii)} \, [/tex], segue que:
[tex]\qquad \alpha+2\left(x-\beta+90^{\circ} \right)+\beta=180^{\circ}[/tex]
[tex]\qquad \alpha+2x-2\beta+180^{\circ} +\beta=180^{\circ}[/tex]
[tex]\qquad \alpha+2x-\beta+180^{\circ}=180^{\circ}[/tex]
[tex]\qquad 2x=180^{\circ}-\alpha+\beta-180^{\circ}[/tex]
[tex]\qquad 2x=\beta-\alpha[/tex]
[tex]\qquad \fcolorbox{black}{#eee0e5}{$x=\dfrac{\beta-\alpha}{2}$} \, .[/tex]
Portanto a alternativa correta é a (B).
Solução elaborada pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
