Clique no botão abaixo para visualizar o problema.
Problema
(Indicado a partir do 2ª série do E. M.)
Em um jogo eletrônico, o objetivo é sair do ponto A e chegar em qualquer ponto do segmento de reta BC, movendo-se sempre para cima ou para a direita sobre a malha da imagem abaixo.
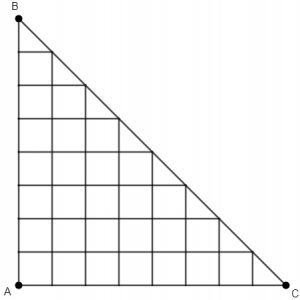
De quantas maneiras um jogador pode alcançar o objetivo desse jogo?
Extraído de Papmem-IMPA.

Lembrete
► Princípio Fundamental da Contagem, ou Princípio Multiplicativo: Se
- uma escolha E1 puder ser feita de [tex] m_1 [/tex] maneiras distintas,
- uma escolha E2 puder ser feita de [tex] m_2 [/tex] maneiras distintas,
- [tex]\cdots[/tex]
- uma escolha Ek puder ser feita de [tex]m_k [/tex] maneiras distintas e
- todas essas escolhas forem independentes entre si (isto é, a escolha de uma não muda a quantidade de possibilidades para a escolha de outra),
então o número total de maneiras de serem feitas sucessivamente essas [tex]k[/tex] escolhas é igual ao produto
[tex]\qquad \qquad \boxed{m_1\times m_2 \times \cdots \times m_k} \, .[/tex]
(Se você não se lembra desse Princípio, seria interessante dar uma passadinha nesta Sala de Estudo.)
Solução
Note que é necessário realizar [tex]8[/tex] movimentos para chegar até o segmento de reta BC, saindo de A, pois só é possível movimentos para cima ou para a direita (não há como “retornar” e nem caminhar em diagonal).
- O jogador vai sair do ponto A.
- Após o primeiro movimento, o jogador estará em um dos pontos assinalados em vermelho na figura abaixo.
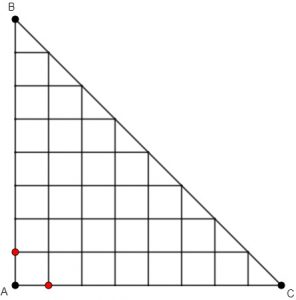
- Estando em qualquer um desses pontos, temos a certeza de que no próximo movimento o jogador estará em um dos pontos em verde.
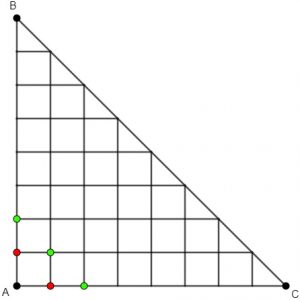
Seguindo esse mesmo raciocínio, note que, para cada movimento, o jogador tem sempre [tex]2[/tex] modos para se deslocar: para cima ou para a direita. Assim:
- para fazer o [tex]1^\circ[/tex] movimento, o jogador tem [tex]2[/tex] opções.
- para fazer o [tex]2^\circ[/tex] movimento, o jogador tem [tex]2[/tex] opções;
- para fazer o [tex]3^\circ[/tex] movimento, o jogador tem [tex]2[/tex] opções;
- para fazer o [tex]4^\circ[/tex] movimento, o jogador tem [tex]2[/tex] opções;
- para fazer o [tex]5^\circ[/tex] movimento, o jogador tem [tex]2[/tex] opções;
- para fazer o [tex]6^\circ[/tex] movimento, o jogador tem [tex]2[/tex] opções;
- para fazer o [tex]7^\circ[/tex] movimento, o jogador tem [tex]2[/tex] opções e
- para fazer o [tex]8^\circ[/tex] movimento, o jogador tem [tex]2[/tex] opções.
Portanto, pelo Princípio Multiplicativo, há [tex]2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2\cdot 2 = 2^{8}=256[/tex] modos de resolver o jogo.
Solução elaborada pelos Moderadores do Blog.
