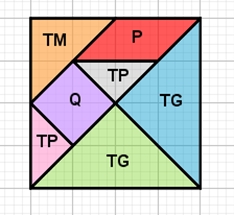
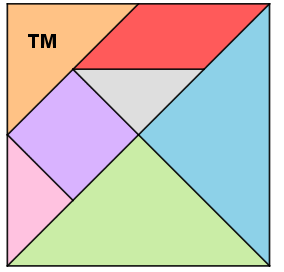
O Tangram é um antigo quebra-cabeça chinês cujo nome significa “sete tábuas da sabedoria”. Ele é composto de sete peças com as seguintes formas geométricas:
- dois triângulos grandes (TG);
- dois triângulos pequenos (TP);
- um triângulo médio (TM);
- um paralelogramo (P);
- um quadrado (Q).
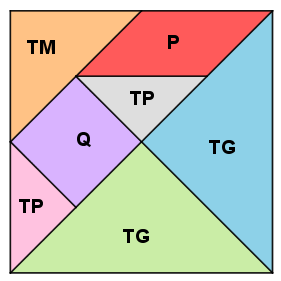
As sete peças do Tangram podem ser combinadas, sem sobreposição, para formar várias e várias figuras: pessoas, animais, plantas, letras, figuras geométricas, entre outras.
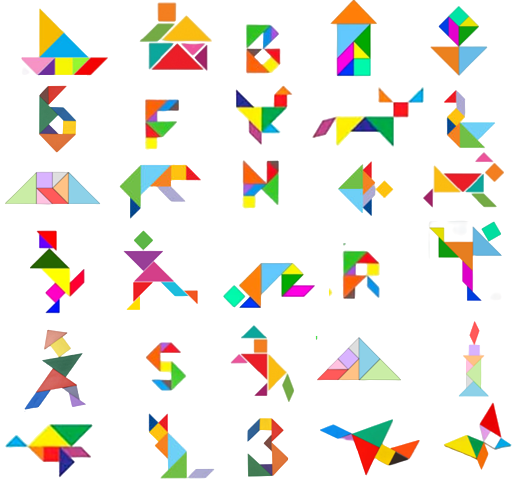
Como o Tangram é uma figura plana, vale a pena explorá-lo no estudo do cálculo de áreas.
Inicialmente, vamos nos concentrar em medir a área delimitada pelo quadrado externo, a partir do qual as peças do Tangram são construídas.
Atividade 4
- Quantos triângulos grandes (TG) cabem dentro do quadrado externo do Tangram? Em termos de unidades de área, o que podemos afirmar a partir dessa resposta?

- Suponha que o nosso Tangram foi desenhado em uma malha quadriculada, com quadradinhos de lados com comprimento de 1 cm. Usando como unidade de área um desses quadradinhos, qual a medida da área definida pelo quadrado externo do Tangram?

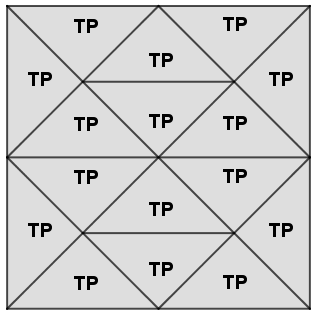
- Utilizando um dos triângulos pequenos (TP) como unidade de área, qual a medida da área definida pelo quadrado externo do Tangram?
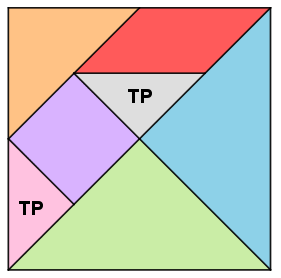
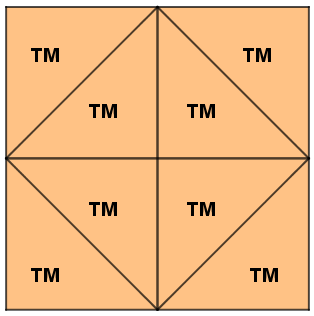
- Usando o triângulo médio (TM) como unidade de área, qual a medida da área definida pelo quadrado externo do Tangram?
Se for conveniente, vocês podem utilizar o applet abaixo para fazer os dois últimos itens desta atividade.
Um applet para ajudar na atividade
Vocês podem utilizar este applet para movimentar os triângulos TM e TP e obter as medidas de área nas quais vocês ficaram em dúvida.
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para transladar um dos triângulos, clique sobre ele com qualquer botão do mouse, mantenha o mouse pressionado e arraste-o. (Se vocês estiverem utilizando um celular ou um tablet, basta tocar levemente no triângulo e fazer o movimento.)
(3) Para rodar o triângulo TM, clique com qualquer botão do mouse sobre o vértice A, mantenha o mouse pressionado e rode-o. (Se vocês estiver utilizando um celular ou um tablet, basta tocar levemente no ponto e fazer o movimento.)
(4) Para rodar o triângulo TP, clique com qualquer botão do mouse sobre o vértice B, mantenha o mouse pressionado e rode-o. (Se vocês estiver utilizando um celular ou um tablet, basta tocar levemente no ponto e fazer o movimento.)
(5) Se quiser voltar para a visualização inicial, clique nas setinhas circulares que aparecem no canto superior direito da janela.
OBMEP_ srdg, criado com o GeoGebra
Atividade 5
Vamos tentar recobrir a superfície interna do quadrado externo do Tangram utilizando a peça quadrada do Tangram.
A princípio, conseguimos recobrir parte da superfície em questão com quatro peças quadradas do Tangram, conforme vemos na figura abaixo, à esquerda. Mas se observarmos a superfície que ficou sem recobrimento, percebemos que conseguimos recobri-la utilizando oito triângulos.

Mas o que acontecerá se rotacionarmos e transladarmos os triângulos T1 , T2 , T7 e T8 , conforme indicado na próxima imagem?

Observem que conseguimos os quadrados Q5 , Q6 , Q7 e Q8.

Pergunta: O procedimento que fizemos garante que a medida da superfície definida pelo quadrado externo do Tangram é igual a 8 vezes a medida da superfície da peça quadrada?
Atividade 6
É possível estabelecer uma comparação entre as medidas das áreas da superfície definida pelo quadrado externo do Tangram e da superfície definida pela peça P (paralelogramo)?
Atividade 7
De acordo com as atividades anteriores, podemos concluir que a medida da área da superfície de cada peça de um Tangram é uma fração da medida da superfície do quadrado externo formado com as sete peças.
Suponha que a medida da área da superfície definida pelo quadrado externo de um Tangram seja 400 cm2. Termine o preenchimento da tabela abaixo.
| Peça do Tangram | Fração da área do quadrado externo | Área em cm2 |
| TP | ||
| TM | 50 | |
| TG | ||
| Q | 1/8 | |
| P |
Atividade 8
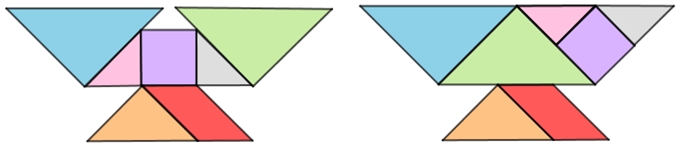
Cada uma das duas figuras mostradas abaixo foram montadas com as sete peças de um Tangram definido a partir de uma malha quadriculada formada por quadradinhos com 1 cm de lado.
Qual superfície tem maior área, a definida pela figura da esquerda ou a definida pela figura da direita?

A próxima atividade não envolve áreas, diretamente; mas é bem divertida!
Vamos lá?
Atividade 9
Podemos encontrar moldes distintos para Tangrans de mesmo tamanho. Além das posições das peças, o que diferencia dois moldes é o possível formato do paralelogramo que compõe o conjunto de peças de cada um, conforme podemos observar na imagem a seguir.
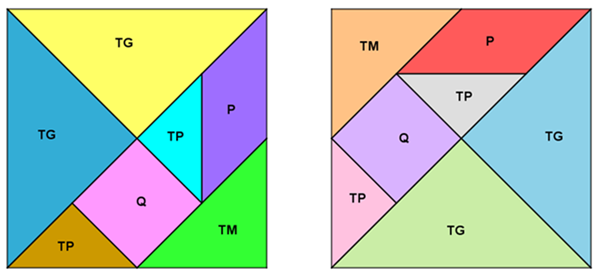
Se só pudermos movimentar as peças desses dois Tangrans sem tirá-las do plano, todas as figuras que construímos com um conjunto de peças são possíveis de serem construídas com o outro conjunto?
Por exemplo, o paralelogramo que aparece na próxima imagem pode ser construído a partir de qualquer um dos conjuntos de peças acima, sem sobreposição.

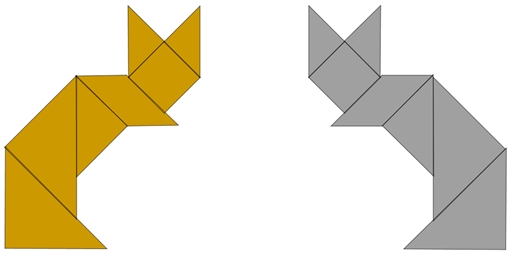
Mas cada um dos gatinhos abaixo também pode ser construído a partir a partir de qualquer um dos conjuntos de peças, sem sobreposição e sem tirar as peças do plano?
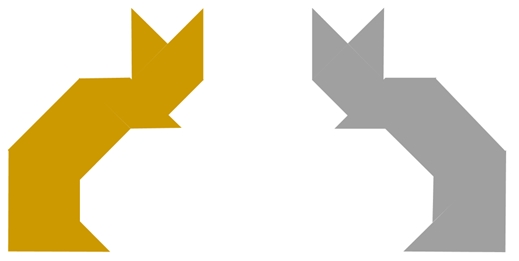
Disponibilizamos aplicativos para vocês fazerem as construções propostas, a partir dos dois moldes de Tangram.
Boa diversão!
Precisam de ajuda para as construções?
Cliquem no botão abaixo!
 |
Se vocês precisarem moldes para construir manualmente um Tangram, cliquem AQUI.
BONS ESTUDOS!!! |
BOA DIVERSÃO!

Equipe COM – OBMEP