Nesta Sala vamos trabalhar com atividades envolvendo superfícies, figuras planas e cálculos de áreas.
Mas antes de mais nada, vamos fazer uma breve observação.
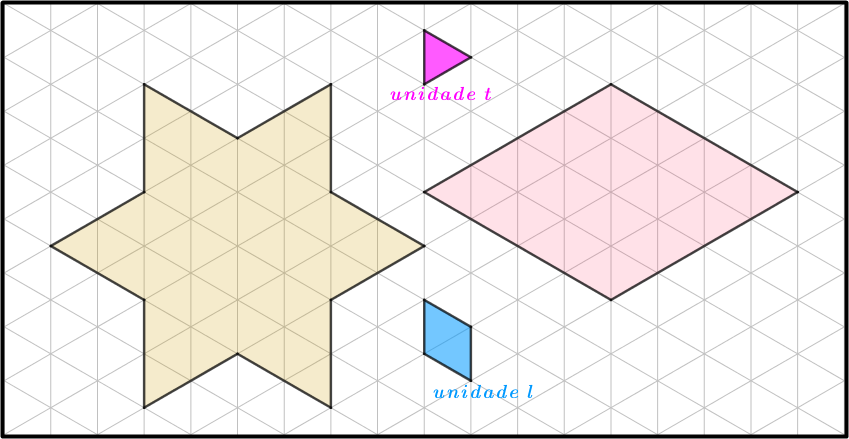
a primeira por um contorno marrom, a segunda por um contorno azul e a terceira por um contorno alaranjado.
➤ Considerando, agora, os contornos das figuras anteriores e também as regiões internas por eles delimitadas, obtemos três novas figuras, que são exemplos de superfícies planas.
Rigorosamente falando, nós medimos áreas de superfícies planas, ou seja, medimos a porção do plano ocupada por essas superfícies. Por essa razão, quando, na nossa conversa, nos referirmos informalmente à área de uma figura plana, formalmente estaremos nos referindo à área da superfície definida por essa figura.
O que é calcular uma área?
“Calcular (ou medir) a área de uma superfície plana” é “medir essa superfície” , ou seja, “medir a porção do plano que essa superfície ocupa” .
E como para calcular a área de uma superfície plana precisamos medir essa superfície, então temos que compará-la com outra superfície previamente estabelecida como unidade de medida (um padrão). Informalmente, o resultado dessa comparação (que chamamos de medida da área) é um número que nos diz “quantas vezes” a unidade de medida utilizada cabe na superfície em questão.
É usual (mas não necessário) adotar como “ 1 unidade de área” a superfície definida por um quadrado unitário.
Assim, um quadrado unitário terá 1 unidade de área.
Neste caso, particularmente, o cálculo da área de uma superfície plana pode ser visto como o cálculo de quantos quadrados unitários cabem nela.
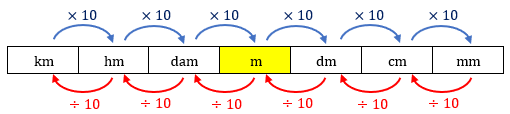
Por falar em unidade de comprimento, é bom lembrar que no Brasil, oficialmente, a unidade padrão de medida de comprimento é o metro, cujo símbolo é m. Para medir comprimentos maiores ou menores usamos, respectivamente, os seus múltiplos (decâmetro, hectômetro e quilômetro) e submúltiplos (decímetro, centímetro e milímetro). Cada uma dessas unidades de comprimento é dez vezes maior (menor) que a unidade imediatamente inferior (superior); logo, podemos transformar qualquer uma delas em outra utilizando o esqueminha abaixo.
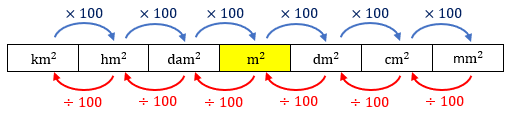
No que tange à medida de área padrão, no Brasil, oficialmente, a unidade padrão de medida de área no sistema métrico decimal é o metro quadrado, cujo símbolo é m2.
Para medir áreas maiores ou menores usamos, respectivamente, os seus múltiplos (decâmetro quadrado, hectômetro quadrado e quilômetro quadrado) e submúltiplos (decímetro quadrado, centímetro quadrado e milímetro quadrado). Cada uma dessas unidades de área é cem vezes maior (menor) que a unidade imediatamente inferior (superior). Também podemos transformar qualquer uma delas em outra utilizando o esqueminha abaixo.
Podemos, então, complementar as informações sobre o famoso quadrado unitário:
Por exemplo: 1 cm, 1 m, 1 km etc.
Assim, um quadrado unitário terá 1 unidade de área.
Por exemplo: 1 cm 2, 1 m 2, 1 km 2 etc.
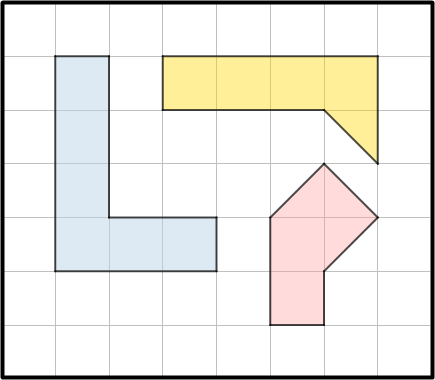
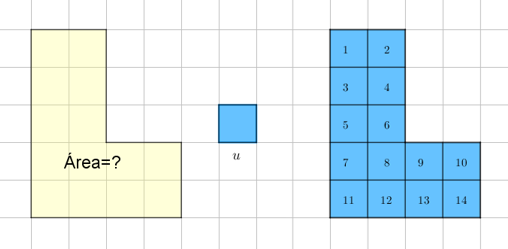
Vamos focar no tema da Sala e considerar, por exemplo, a superfície na forma de L colorida de amarelo na figura abaixo. Vamos medir a área dessa superfície usando como unidade de medida o quadradinho azul u.
Verificamos que a unidade u cabe 14 vezes no L amarelo; dessa forma, se denotarmos por A a medida da área da superfície amarela, temos que:
A = 14 u.
Se tivéssemos a informação de que o quadradinho azul u tem lados medindo 1 cm, por exemplo, então a área do quadradinho u mediria 1 cm2 e teríamos
A = 14 cm2.
Por outro lado, perceba que se considerássemos a mesma superfície na forma de L colorida de amarelo, mas, ao medirmos a área dessa superfície, usássemos como unidade de medida o triângulo alaranjado t, verificaríamos que a unidade t cabe 28 vezes no L amarelo. Portanto, neste caso, teríamos que:
A = 28 t.
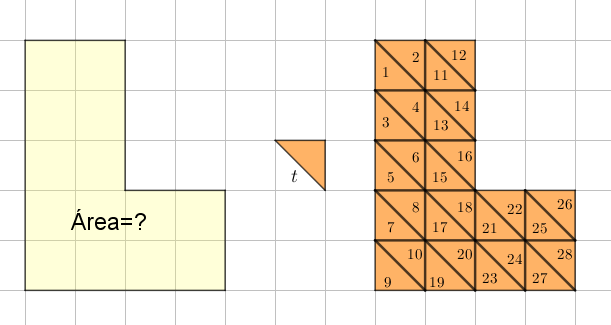(Observe que o triângulo alaranjado não é, obviamente, um quadradinho unitário.)
Vamos exercitar um pouco essa ideia de, conhecida uma unidade de medida, usá-la para obter medidas de áreas de superfícies planas, sem necessariamente usarmos um quadradinho unitário como unidade de medida.
É só clicar nos botões abaixo.
Vocês conhecem o Tangram?
As nossas próximas atividades envolvem esse quebra-cabeça milenar. Vamos abrir uma página só para ele!
Para visitá-la, cliquem no próximo botão; depois vocês podem voltar para esta página, usando o link no final da página do Tangram.
E aí, gostaram?
Usar quadradinhos unitários para medir áreas é até divertido; mas utilizar quadradinhos para calcular áreas de superfícies planas extensas é muito trabalhoso e, às vezes, até impossível!
Imagine calcular a área de um campo de futebol ou da parede externa de um edifício bem alto utilizando quadrados unitários com lados medindo 1 m ?
Haja quadradinhos, hem? (… E olhos para enxergar e contar!)
Imagens adaptadas de Wikipédia e Freepik, respectivamente. (Acesso em 30/05/23)
Mas os quadradinhos unitários podem nos ajudar, se usarmos um pouco de imaginação e raciocínio! Vejamos como.
- Começando pelo campo de futebol:
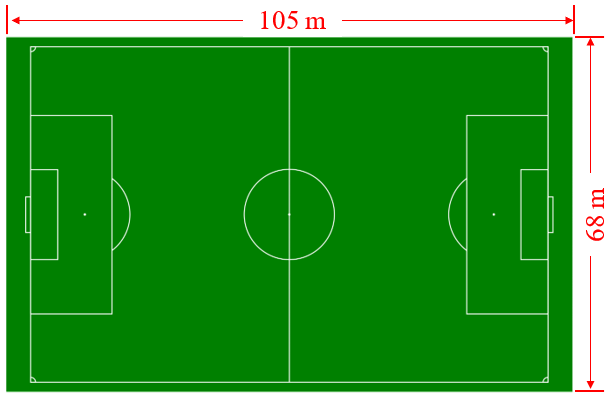
- No lado cujo comprimento mede 105 m, vamos imaginar uma fileira com 105 quadrados unitários, cada um medindo 1 m2 de área.
- Repetindo essa fileira, uma abaixo da outra, 68 vezes, conseguimos recobrir o campo todo, não é?
- Assim, conseguimos recobrir um campo de futebol de 105 m por 68 m com 105 ✕ 68 = 7 140 quadrados unitários, cada um medindo 1 m2 de área.
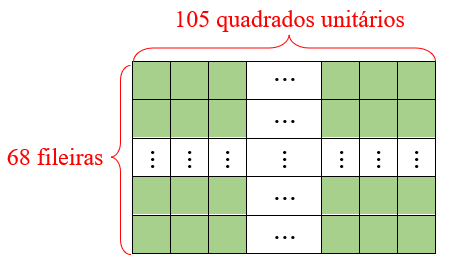
Portanto, a medida da área (ou simplesmente a área) do campo de futebol em questão é 7 140 m2.
- E a medida da área da parede externa de um edifício?
Esse cálculo vai ficar para vocês, na próxima atividade!
Para calcular a área de uma figura plana no nosso dia a dia, na maioria das vezes utilizamos fórmulas específicas que dependem do formato das figuras com as quais estamos lidando. As principais figuras planas são o retângulo, o quadrado, o triângulo, o paralelogramo, o trapézio e o círculo, e cada uma dessas figuras possui uma fórmula para o cálculo de sua área.
Conhecer essas fórmulas é necessário para resolver muitos problemas principalmente por reduzir o tempo de resolução deles!
Na figura abaixo, temos uma revisão das fórmulas para o cálculo de áreas das figuras planas mais comuns.
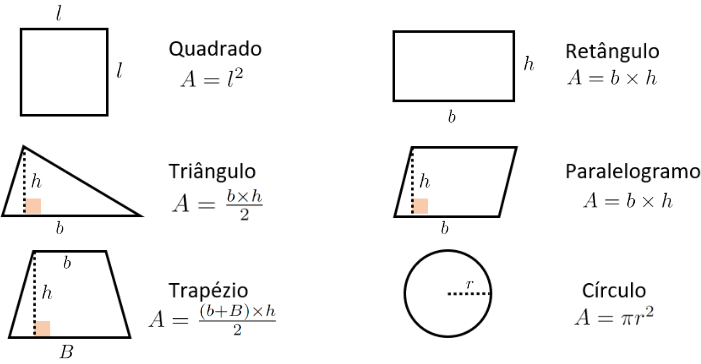
Mas até para entender como algumas dessas fórmulas medem, de fato, a área da superfície de uma figura, como elas se propõem, podemos usar os quadrados unitários.
Ficaram curiosos(as)?
Então, cliquem no último botão desta Sala e
Bons estudos!!!!
Equipe COM – OBMEP