Clique no botão abaixo para visualizar o problema.
Problema
(A partir do 9º ano do E. F.) (Nível: Médio)
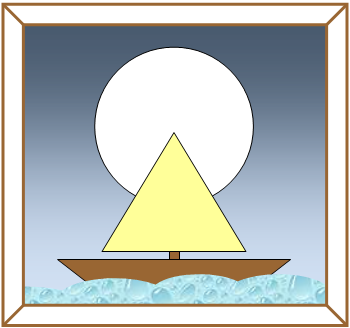
(OPM 2004 – adaptado) O pescador Pedro gosta muito de pescar em noites de lua cheia e por isso sua amiga Maria pintou o quadro que aparece na imagem abaixo para presenteá-lo.
A vela do barco é um triângulo equilátero com [tex]20 \, \text{cm}[/tex] de lado e a lua é um círculo com centro em um vértice do triângulo.
Se a área da parte da lua escondida atrás da vela é a metade da área da vela, qual é o raio da lua que Maria pintou?

Lembretes
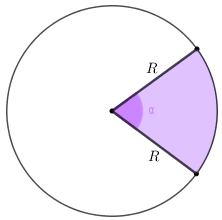
✐ Área de um setor circular de raio [tex]R[/tex] e [tex]\alpha[/tex] graus:
[tex]\qquad \qquad \boxed{A_{setor}=\dfrac{\pi \cdot \alpha \cdot R^{ \, 2} }{360}}[/tex]
(Para aprender um pouco mais sobre setor circular, cliquem AQUI)
Solução
Seja [tex]R[/tex] a medida do raio a ser calculada.
Vamos inicialmente determinar a área da vela, já que a área da parte da lua escondida atrás da vela é a metade dessa área.
Como a vela é um triângulo equilátero, podemos utilizar o Teorema de Pitágoras para encontrar a altura do triângulo.
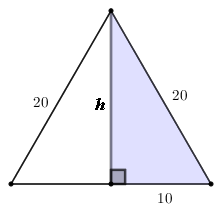
Sabemos que em um triângulo equilátero toda altura é também uma mediana; assim, se [tex]h[/tex] for a altura da vela, segue que:
[tex]\quad h^2+10^2=20^2 [/tex]
[tex]\quad h^2=300[/tex]
[tex]\quad \boxed{h=10\sqrt{3}\, \text{cm}}[/tex].
Dessa forma, temos que a área da vela é dada por:
[tex]\quad A_v=\dfrac{base\times altura}{2}[/tex]
[tex]\quad A_v=\dfrac{20\times 10\sqrt{3}}{2}[/tex]
[tex]\quad \boxed{A_v= 100\sqrt{3}\,\text{cm}^2}[/tex].
A partir daqui podemos concluir a solução do problema de duas maneiras; vejamos.
[tex]\textcolor{#800000}{(i)}[/tex] Se você sabe o que é um setor circular, observe que a parte da lua escondida é um setor circular e, portanto, podemos utilizar a fórmula do Lembrete: [tex]A_{setor}=\dfrac{\pi \cdot \alpha \cdot R^{ \, 2} }{360}[/tex].
Como a área da parte da lua escondida é a metade da área da vela, temos que [tex]A_{setor}=\dfrac{A_v}{2}[/tex] e, assim,
[tex]\quad \boxed{\dfrac{\pi \cdot \alpha \cdot R^{ \, 2}}{360}= \dfrac{100\sqrt{3}}{2}}[/tex].
Por outro lado, note que o ângulo central que define o setor circular é um ângulo interno de um triângulo equilátero, logo:
[tex]\quad \alpha=\dfrac{180^\circ}{3}=60^\circ[/tex]
e, portanto, segue que:
[tex]\quad \dfrac{\pi \cdot 60 \cdot R^{ \, 2} }{360}= \dfrac{100\sqrt{3}}{2}[/tex]
[tex]\quad \dfrac{\pi \cdot R^{ \, 2} }{6}= 50\sqrt{3}[/tex]
[tex]\quad R^{ \, 2}= \dfrac{300\sqrt{3}}{\pi}[/tex]
[tex]\quad R= \sqrt{\dfrac{300\sqrt{3}}{\pi}}[/tex].
Pelo exposto, temos que a medida do raio da lua pintada por Maria é [tex] \, \fcolorbox{black}{#eee0e5}{$R= 10\sqrt{\dfrac{3\sqrt{3}}{\pi}} \approx 12,86 \; \text{cm}$} \, [/tex].
[tex]\textcolor{#800000}{(ii)}[/tex] Se você não sabe o que é um setor circular, podemos resolver o problema sem a fórmula do Lembrete.
Para isso basta observar que, como a medida de cada ângulo interno de um triângulo equilátero, e particularmente da vela, é [tex]\alpha=\dfrac{180^\circ}{3}=60^\circ[/tex] e [tex]60^\circ=\dfrac{360^\circ}{6}[/tex], então a área da parte da lua que está escondida atrás da vela é um sexto da área total do círculo cuja medida [tex]R[/tex] do raio queremos determinar.
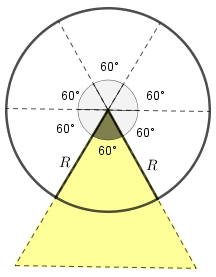
Como a área da parte da lua escondida é a metade da área da vela, a qual já sabemos ser [tex]A_v= 100\sqrt{3}\,\text{cm}^2[/tex], temos que [tex]\dfrac{100\sqrt{3}}{2}=\dfrac{\pi \cdot R^2}{6}[/tex], donde segue que:
[tex]\quad 300\sqrt{3}=\pi \cdot R^2[/tex]
[tex]\quad R^2=\dfrac{300\sqrt{3}}{\pi}[/tex]
[tex]\quad R=\sqrt{\dfrac{300\sqrt{3}}{\pi}}[/tex].
Assim, a medida do raio da lua pintada por Maria é [tex] \, \fcolorbox{black}{#eee0e5}{$R= 10\sqrt{\dfrac{3\sqrt{3}}{\pi}} \approx 12,86 \; \text{cm}$} \, [/tex].
Soluções elaboradas pelos Moderadores do Blog.
 |
Se for conveniente, você pode obter um arquivo PDF desta página, com o problema e a solução, clicando no botão abaixo. |
