(A) Problema para ajudar na escola: Área de uma figura estranha

Problema
(A partir do 9º ano do E. F.) (Nível: médio)

(OBMEP 2012) O retângulo mostrado abaixo foi desenhado em papel quadriculado e mede [tex]4 \, \text{cm}[/tex] de largura por [tex]5 \, \text{cm}[/tex] de altura.

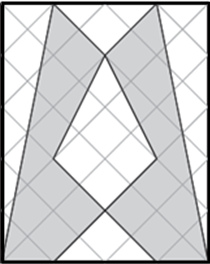
Qual é a área da região cinza?

(a) [tex]10 \text{ cm}^2[/tex]

(b) [tex]11\text{ cm}^2[/tex]

(c) [tex]12,5 \text{ cm}^2[/tex]

(d) [tex]13 \text{ cm}^2[/tex]

(e) [tex]14,5 \text{ cm}^2[/tex]

Solução 1

Na figura desenhada no papel quadriculado, trace os segmentos de reta [tex]s_1, \, s_2 \, [/tex] e [tex] \, s_3[/tex], conforme mostrado na imagem a seguir.

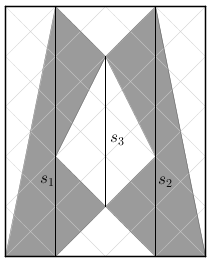
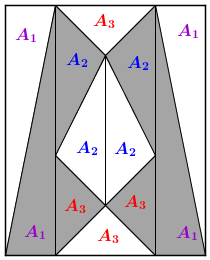
Observe, na figura ao lado, que ficaram definidos doze triângulos, quatro a quatro congruentes:

• quatro triângulos com área [tex]{\textcolor{#8B008B}{A_1}}[/tex];
• quatro triângulos com área [tex]{\textcolor{blue}{A_2}}[/tex];
• quatro triângulos com área [tex]{\textcolor{red}{A_3}}[/tex].

Assim, podemos observar que:

• a área total da região branca, [tex]A_b[/tex], é dada por [tex]A_b=2{\textcolor{#8B008B}{A_1}}+2{\textcolor{blue}{A_2}}+2{\textcolor{red}{A_3}}[/tex];
• a área total da região cinza, [tex]A_c[/tex], é dada por [tex]A_c=2{\textcolor{#8B008B}{A_1}}+2{\textcolor{blue}{A_2}}+2{\textcolor{red}{A_3}}[/tex].

Como [tex]A_b=A_c[/tex] e o retângulo inicialmente desenhado mede [tex]4 \text{ cm}[/tex] de largura por [tex]5 \text{ cm}[/tex] de altura, então
[tex]\qquad \boxed{A_c=\dfrac{4 \times 5}{2}= 10 \, \text{ cm}^2}[/tex],
ou seja, a alternativa (a) é a correta.

Solução elaborada pelos Moderadores do Blog.

Um aplicativo para ajudar

Você pode utilizar o applet abaixo para observar que, de fato:

• os quatro triângulos assinalados na figura inicial com [tex]{\textcolor{#8B008B}{A_1}}[/tex] são congruentes;
• os quatro triângulos assinalados na figura inicial com [tex]{\textcolor{blue}{A_2}}[/tex] são congruentes;
• os quatro triângulos assinalados na figura inicial com [tex]{\textcolor{red}{A_3}}[/tex] são congruentes.

Sabemos que, na prática, dois triângulos são congruentes se podem ser sobrepostos por meio de deslocamentos convenientes. Assim, movimente os triângulos lilás, vermelho ou azul desenhados fora do quadriculado, um de cada vez, e tente colocá-los sobre os quatro triângulos desenhados na figura inicial e com a respectiva identificação [tex]{\textcolor{#8B008B}{A_1}}[/tex] , ou [tex]{\textcolor{blue}{A_2}}[/tex], ou [tex]{\textcolor{red}{A_3}}[/tex].

Solução 2

Agora, se você só se convence com números, ou gosta mesmo é de fazer continhas, observe que a diagonal de cada quadradinho do papel quadriculado mede [tex]1 \text{ cm}[/tex], já que, por exemplo, um dos lados do retângulo inicialmente desenhado é formado por quatro diagonais e mede [tex]4 \, \text{cm}[/tex].
Perceba que a parte cinza é constituída de:

• dois triângulos retângulos cujos catetos medem [tex]1 \text{ cm}[/tex] e [tex]5 \text{ cm}[/tex] e cujas áreas denotamos por [tex]{\textcolor{#8B008B}{A_1}}[/tex];
• dois triângulos não retângulos, com um dos lados medindo [tex]3 \, \text{cm}[/tex] e as respectivas alturas com [tex]1 \text{ cm}[/tex], cujas áreas denotamos por [tex]{\textcolor{blue}{A_2}}[/tex];
• dois triângulos retângulos com hipotenusas medindo [tex]2 \, \text{cm}[/tex] cada e as respectivas alturas medindo [tex]1 \, \text{cm}[/tex], cujas áreas denotamos por [tex]{\textcolor{red}{A_3}}[/tex].

Assim, temos que:

• [tex]{\textcolor{#8B008B}{A_1=\dfrac{5 \times 1}{2}=\dfrac{5}{2}}}[/tex];
• [tex]{\textcolor{blue}{A_2=\dfrac{3 \times 1}{2}=\dfrac{3}{2}}}[/tex];
• [tex]{\textcolor{red}{A_3=\dfrac{2 \times 1}{2}=1}}[/tex];

donde a área da região cinza é dada por:

[tex]\qquad A_c=2A_1+2A_2+2A_3=5+3+2=10 \, \text{cm}^2[/tex].

Solução elaborada pelos Moderadores do Blog.