✏ Link do problema para dispositivos da Apple.
Problema
(Indicado a partir do 7º ano do E. F.)
Em um Congresso Internacional de Matemáticos, cada participante apertou as mãos de um certo número de outras pessoas.
Duas pessoas não se cumprimentaram mais de uma vez e os números de apertos de mãos que cada pessoa deu não são necessariamente iguais.
Explique porque a quantidade de pessoas que apertaram as mãos um número ímpar de vezes deve ser um número par.
Adaptado de The USSR Olympiad Problem Book; DO Shklarsky, NN Chentzov e IM Yaglom.

Ajuda
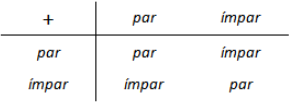
Em várias situações é possível determinarmos a paridade de expressões envolvendo números naturais, a partir da paridade desses números, sem sequer calcular as expressões.
Particularmente, a tabelinha abaixo ilustra situações de paridade que irão aparecer na solução deste problema:
- A soma de dois números naturais de mesma paridade é par.
- A soma de dois números naturais de paridade oposta é ímpar.
(Se precisar, visite esta Sala.)
Solução
Considere [tex]S[/tex] a soma total das quantidades de apertos de mãos dos participantes; isto é, some as quantidades de apertos de mãos que cada pessoa deu.
- Este número [tex]S[/tex] é par, porque cada aperto de mão é realizado por duas pessoas, sendo contado duas vezes ao somarmos as quantidades.
Para compor esta soma [tex]S[/tex], que é par, podemos considerar dois grupos de parcelas: as pares (isto é, as quantidades dos apertos de mãos de pessoas que realizaram um número par de cumprimentos) e as ímpares (quantidades dos apertos de mãos de pessoas que realizaram um número ímpar de cumprimentos).
Observe o esquema:
[tex]\qquad \qquad S=\textcolor{red}{\underbrace{\left(~~+~~+\cdots+~~+~~\right)}_{\text{soma de parcelas pares}}}+\textcolor{#0000FF}{\underbrace{\left(~~+~~+\cdots+~~+~~\right)}_{\text{soma de parcelas ímpares}}}\,[/tex].
- Como a soma de números pares é sempre par, as parcelas pares somam um número par.
[tex]\qquad \qquad \underbrace{S}_{\text{par}}=\underbrace{\boxed{\textcolor{red}{\underbrace{\left(~~+~~+\cdots+~~+~~\right)}_{\text{soma de parcelas pares}}}}}_{\text{par}}+\underbrace{\boxed{\textcolor{#0000FF}{\underbrace{\left(~~+~~+\cdots+~~+~~\right)}_{\text{soma de parcelas ímpares}}}}}_{\text{???}}[/tex].
Logo, para que a soma total [tex]S[/tex] seja, de fato, par,
- as parcelas ímpares também devem totalizar uma soma par.
Mas isso só ocorre se houver uma quantidade par destas parcelas ímpares, pois a soma de uma quantidade ímpar de números ímpares é ímpar e a soma de uma quantidade par de números ímpares é par (verifique!).
Conclui-se, então, o enunciado: a quantidade de pessoas que apertaram as mãos um número ímpar de vezes deve ser uma quantidade par.
Solução elaborada pelos Moderadores do Blog.
