Problema – Todo triângulo é isósceles!
Afirmação: Todo triângulo é isósceles.
Justificativa:
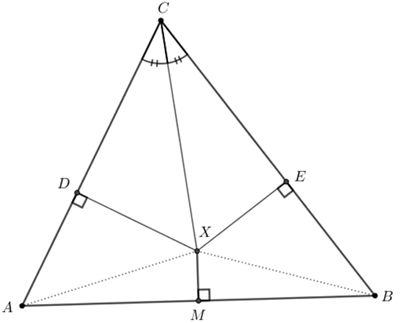
(1) Tome um triângulo qualquer [tex]ABC[/tex].
(2) Trace a bissetriz do ângulo [tex]A\hat C B[/tex] e a mediatriz do segmento [tex]\overline{AB}[/tex], indicando por [tex]X[/tex] a interseção das mesmas.
(3) Trace os segmentos [tex]\overline{XD}[/tex] e [tex]\overline{XE}[/tex] perpendiculares aos lados [tex]\overline{CA}[/tex] e [tex]\overline{CB}[/tex], respectivamente, e trace também os segmentos [tex]\overline{XA}[/tex] e [tex]\overline{XB}[/tex].
(4) Os triângulos [tex]CXD[/tex] e [tex]CXE[/tex] são congruentes pelo caso ALA; portanto, [tex]\overline{CD}[/tex] e [tex]\overline{CE}[/tex] são congruentes e [tex]\overline{XD}[/tex] e [tex]\overline{XE}[/tex] também são congruentes.
(5) Como [tex]X[/tex] está na mediatriz de [tex]\overline{AB}[/tex], temos [tex]\overline{XA}[/tex] e [tex]\overline{XB}[/tex] congruentes.
(6) Os triângulos [tex]XDA[/tex] e [tex]XEB[/tex] são congruentes pelo caso LAL; portanto, [tex]\overline{DA}[/tex] e [tex]\overline{EB}[/tex] são congruentes.
(7) Finalmente, [tex]CA = CD + DA = CE + EB = CB[/tex] e, portanto, o triângulo [tex]ABC[/tex] é isósceles.
Identifique o erro cometido nessa argumentação.
 |
Tente encontrar o erro da argumentação apresentada utilizando o applet abaixo!
|
Um applet para ajudar
Na janela inicial do aplicativo, você visualizará um triângulo [tex]ABC[/tex], a bissetriz do ângulo [tex]A\hat{C}B[/tex], a mediatriz do segmento [tex]\overline{AB}[/tex], o ponto [tex]\textcolor{#0000FF}{M}[/tex]- ponto médio do segmento [tex]\overline{AB}[/tex] – e o ponto [tex]\textcolor{red}{I}[/tex], interseção da bissetriz e da mediatriz em questão.
Você poderá movimentar os pontos [tex]A[/tex], [tex]B[/tex] e [tex]C[/tex], modificando assim o triângulo inicial.
A dica é: observe o ponto de interseção [tex]I[/tex].
Instruções:
(1) Espere o applet carregar. (O aplicativo pode demorar um pouquinho para carregar.)
(2) Para movimentar os pontos [tex]A[/tex], [tex]B[/tex] ou [tex]C[/tex], basta clicar sobre cada um deles com qualquer botão do mouse, manter esse botão pressionado e fazer o movimento lentamente. (Se você estiver utilizando um celular ou um tablet, basta tocar levemente no ponto a ser movimentado e fazer o movimento.)
(3) Se precisar retornar à configuração inicial, clique nas setinhas que aparecem no canto superior direito do aplicativo.
OBMEP_ srdg, criado com o GeoGebra
 |
Para ver uma solução deste problema, clique aqui .
|
Equipe COM – OBMEP
