Problema
(Indicado a partir do 9º ano do E. F.)
Afirmação: Todo triângulo é isósceles.
Justificativa:
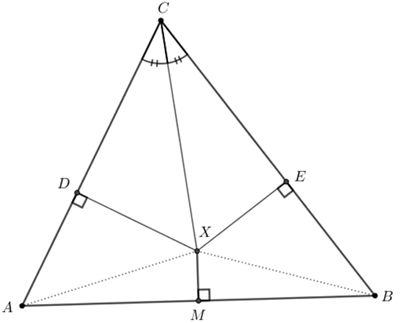
(1) Tome um triângulo qualquer [tex]ABC[/tex].
(2) Trace a bissetriz do ângulo [tex]A\hat C B[/tex] e a mediatriz do segmento [tex]\overline{AB}[/tex], indicando por [tex]X[/tex] a interseção das mesmas.
(3) Trace os segmentos [tex]\overline{XD}[/tex] e [tex]\overline{XE}[/tex] perpendiculares aos lados [tex]\overline{CA}[/tex] e [tex]\overline{CB}[/tex], respectivamente, e trace também os segmentos [tex]\overline{XA}[/tex] e [tex]\overline{XB}[/tex].
(4) Os triângulos [tex]CXD[/tex] e [tex]CXE[/tex] são congruentes pelo caso ALA; portanto, [tex]\overline{CD}[/tex] e [tex]\overline{CE}[/tex] são congruentes e [tex]\overline{XD}[/tex] e [tex]\overline{XE}[/tex] também são congruentes.
(5) Como [tex]X[/tex] está na mediatriz de [tex]\overline{AB}[/tex], temos [tex]\overline{XA}[/tex] e [tex]\overline{XB}[/tex] congruentes.
(6) Os triângulos [tex]XDA[/tex] e [tex]XEB[/tex] são congruentes pelo caso LAL; portanto, [tex]\overline{DA}[/tex] e [tex]\overline{EB}[/tex] são congruentes.
(7) Finalmente, [tex]CA = CD + DA = CE + EB = CB[/tex] e, portanto, o triângulo [tex]ABC[/tex] é isósceles.
Identifique o erro cometido nessa argumentação.


Notações e Lembrete
(I) Denotaremos o segmento de reta definido por dois pontos, digamos [tex]G[/tex] e [tex]H[/tex], por [tex]\overline{GH}[/tex] e seu respectivo comprimento por [tex]GH[/tex].
(II) Teorema da bissetriz interna: A bissetriz de um ângulo interno de um triângulo divide o lado oposto a esse ângulo em segmentos proporcionais aos respectivos lados adjacentes.
Solução
Se nos guiarmos pela figura apresentada no enunciado do problema, veremos duas falhas iniciais na argumentação:
► a congruência dos triângulos [tex]CXD[/tex] e [tex]CXE[/tex] é garantida pelo caso LAAo e não pelo caso ALA;
► a congruência dos triângulos [tex]XDA[/tex] e [tex]XEB[/tex] é garantida pelo caso especial (triângulos retângulos com hipotenusa e um cateto ordenadamente congruentes).
Entretanto, isso não invalidaria a conclusão final.
O principal erro na argumentação é que o ponto [tex]X[/tex], quando determinado, não está no interior do triângulo [tex]ABC[/tex], como mostra a figura proposta. Vejamos o porquê disso.
- (a) Caso tenhamos [tex]CA = CB[/tex], a bissetriz interna relativa a [tex]\overline{AB}[/tex] está contida na mediatriz de [tex]\overline{AB}[/tex], não estando o ponto [tex]X[/tex] determinado.
(b) Caso tenhamos [tex]CA \lt CB[/tex], a bissetriz interna relativa a [tex]\overline{AB}[/tex] intersecta esse lado num ponto [tex]N[/tex].
Pelo Teorema da bissetriz interna, temos [tex]\boxed{\dfrac{NA}{NB}=\dfrac{CA}{CB} \lt 1}[/tex]; logo [tex]NA \lt NB[/tex], ou seja, [tex]N[/tex] está entre [tex]A[/tex] e [tex]M[/tex] (ponto médio de [tex]\overline{AB}[/tex]).
Deste modo, a bissetriz de [tex]A\hat{C}B[/tex], intersecta a mediatriz de [tex]\overline{AB}[/tex] num ponto [tex]X[/tex] externo ao triângulo [tex]ABC[/tex].
Refazendo a figura, com a hipótese (b), veremos que [tex]A[/tex] estará entre [tex]D[/tex] e [tex]C[/tex] e, nesse caso, na etapa (7) teremos [tex]CA = CD-DA[/tex] e não [tex]CA = CD + DA[/tex], invalidando assim a conclusão final.
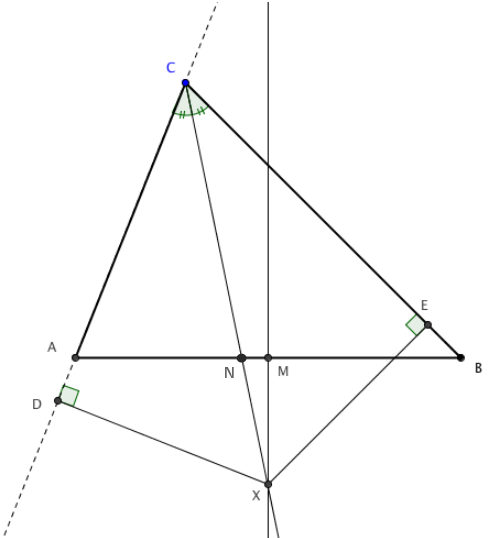
(c) O caso em que [tex]CA \gt CB[/tex], segue de modo análogo ao caso (b).
Solução elaborada pelos Moderadores do Blog .
Dois applets para ajudar…
Com este primeiro applet, você poderá comparar a construção geométrica incorreta que foi apresentada no enunciado do problema com a construção correta.
Com este segundo applet, você poderá observar a afirmação demonstrada na solução do problema de que, em um triângulo [tex]ABC[/tex] qualquer, a bissetriz de [tex]A\hat{C}B[/tex] intersecta a mediatriz de [tex]\overline{AB}[/tex] em um ponto externo ao triângulo, em quantos triângulos você quiser!
